두 점 사이의 거리

- 개요 -
드디어 수학 상의 마지막 대단원인 도형 단원에 들어왔다.
도형을 분석하는 방법을 배우겠다는것이다.
여기서는 도형을 어떻게 분석할거냐면
단원 이름이 '도형의 방정식'이다.
즉 도형을 식을 이용해서 분석할것이다.
다항식 방정식 부등식 배웠으니
이 재료를 가지로 도형에 써먹어볼 시간인것이다.
그리고 첫시간인 이번엔
'두 점 사이의 거리'를 구해볼것이다.
- 수직선 위의 두 점 사이의 거리 -
우선 수직선 위의 두 점 사이의 거리부터 다뤄볼것이다.

이건 너무 간단하다.
두 점의 좌표의 차이가 곧 거리이다.
두 점의 좌표를 서로 빼준다음
거리는 음수가 되면 안되니까 절댓값을 씌운다.
직접 해볼까?

점 A, B가 있다.
점 A는 x=1에 있고, 점 B는 x=6에 있다.
A와 B 사이의 거리는?
두 점의 좌표를 서로 빼준다음 절댓값을 씌운다.
따라서 답은 |1-6| = 5
- 연습 -

두 점의 좌표를 서로 빼준다음 절댓값을 씌운다.
따라서 답은 |-3-5| = 8
- 좌표평면에서의 두 점 사이의 거리 -

여기서 A와 B 사이의 거리를 구해보자.
우선 A와 B 사이의 거리라는게 뭔가?
A에서 B로 가는 최단경로가 있다면, 그것의 길이가 바로 거리이다.
즉 최단거리 = 두 점 사이의 거리
그니까 A에서 B를 향해 그냥 선을 쭉 그으면
그 선분의 길이가 A와 B 사이의 거리이다.

저 선분의 길이만 알아내면 된다.
알아내는 방법은
피타고라스정리의 응용이다.

점 A에서 x축과 평행하게 B를 향해 선을 긋고
점 B에서 y축과 평행하게 A를 향해 선을 그으면
저렇게 수직으로 만나게된다.
따라서 A와 B 사이의 거리 를 빗변으로 하는 직각삼각형이 만들어진다.


직각삼각형만 떼서 가져왔다.
밑변의 길이는 얼마인가?
A와 B 사이의 x좌표 차이이다.
A에서 B를 향해 x축과 평행하게 그었기때문이다.
따라서 밑변의 길이는 |1-4| = 3 이다.
높이의 길이는 얼마인가?
A와 B 사이의 y좌표 차이이다.
B에서 A를 향해 y축과 평핵하게 그었기때문이다.
따라서 높이의 길이는 |1-3| = 2 이다.

직각삼각형에서 두 변의 길이를 알아냈으니
피타고라스 정리를 이용하면 나머지 한 변의 길이도 알아낼 수 있다.

따라서 A와 B 사이의 거리는 √(13) 이다.
결론내자면,
좌표평면 위의 두 점 사이의 거리를 구할때는
피타고라스정리를 이용한다.
밑변의 길이 = x좌표의 차이
높이의 길이 = y좌표의 차이
- 연습 -

점 O와 점 A의 x좌표 차이 = 3
점 O와 점 A의 y좌표 차이 = 4
따라서 두 점 사이의 거리를 구하기 위해
피타고라스 정리를 이용하면
(거리)² = 3²+4² = 25
따라서 두 점 사이의 거리는 5
따라서 답은 5
- 일반화 -
좌표평면 위의 두 점 A(x₁, y₁), B(x₂, y₂) 사이의 거리는
(거리)² = (x좌표 차이)² + (y좌표 차이)²
x좌표 차이 = |x₁-x₂|
y좌표 차이 = |y₁-y₂|
둘다 위 식에 대입하고
양변에 제곱근을 취하면

- 예제 -

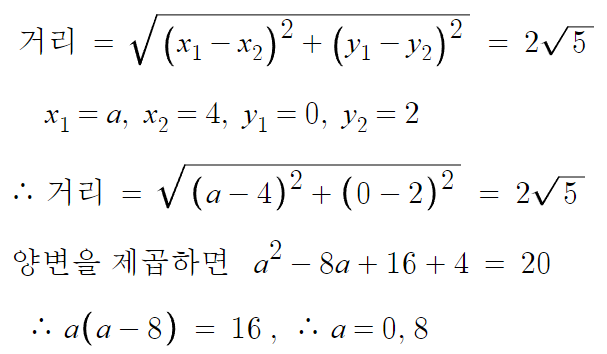
따라서 답은 0, 8