
많은 학생을 수포자로 만든 주제중 하나이다.
- 다항식의 나눗셈 심화 : 나머지만 구하고 싶을때 -
나머지정리를 하기 전에,
우선 나머지정리가 뭐하는건지 가볍게 보여주겠다.
예를 들어, 아래와 같은 문제가 나왔다고 해보자.

다항식의 나눗셈이긴 한데,
굳이 나눗셈을 해보지 않고도 나머지를 알수 있다.
솔직히 일일이 나누고있기 귀찮지 않은가?
일단 우리가 전에 했던 다항식의 나눗셈을 복습해보자.
다항식의 나눗셈연산은 아래와 같이 등식으로 표현할수 있다.

그리고 이건 항상 성립하므로 '항등식'이다.
즉 다항식의 나눗셈연산을 항등식으로 표현할수 있다.

여기서 몫을 Q(x)라 쓸것이다.
Q(x)는 그냥 몫이니까 Q라고 쓰는건데
Q가 x에 대한 다항식이니까 Q(x)라고 쓰자고 약속한거다.
나머지도 같은 논리로 R(x)라고 쓸수 있는데
여기서는 '일차식으로 나눈것' 이므로
나머지가 상수일것이다.
따라서 여기서는 R(x)보단 그냥 R이라 쓸것이다.
나머지는 상수라서 x값에 관계없이 항상 같은값을 가질거기 때문이다.

위 식은 '항등식'이다.
따라서 x에 어떤 값을 대입하든 항상 성립한다.
우리가 하고자 하는건
'몫을 구하지 않고 나머지를 구하기' 이다.
즉 Q(x)를 구하지 않을것이다.
그럼 어떻게하냐면

이 부분이 0이 되도록 해버리면 된다.

그럼 이렇게 되고 몫을 구하지 않고도 나머지를 알아낼수 있다.
근데 어떻게 0으로 만드느냐?
x-1로 나눌거니까
x-1=0 이 되도록 하는 x값을 찾아서 대입해주면 된다.
항등식이라서 x값을 아무거나 대입해도 등식은 계속 성립하기 때문에
가능한 방법이다.
x-1=0 이 되도록 하는 x값은 1이다.
따라서

이 항등식에 x=1을 대입하면
아래와 같이 된다.

따라서 R=2 이고 나머지는 2이다.

따라서 이문제의 답은 2
- 하나 더 해보자 -

중간점검 예제로 넣어주려했는데
그러기엔 좀 어려운거같아서 일단 풀어준다.
1. 우선 항등식으로 나타낸다.

2. 몫을 구하기는 귀찮으니까
x에 적당한 수를 대입하여
몫 자리를 0으로 만들어버린다.

위 식처럼 되려면 (x-1)(x-2)=0 이어야한다.
그러려면 x=1 이거나 x=2 이어야한다.
둘중 아무거나 대입해도 되는데
난 x=1부터 대입할것이다.

여기서 주의할건
바로 나머지는 -1입니다. 하면 안된다.
일차식으로 나눈게 아니라
이차식으로 나눈거기 때문에
나머지가 일차식이 나왔을수도 있기때문이다.
일차식은 일차항과 상수항으로 이루어진 다항식이다.
따라서 만약 나머지가 일차식이라면
x값에 따라 나머지의 값이 바뀔것이다.
내가 처음에 항등식 세울때도 R이라 쓰지 않고 R(x)라 쓴게 이 이유이다.
아무튼 R(x)는 일차식일수도 있으니
일차항의 계수를 a, 상수항을 b라 하면
아래와 같이 식을 세울수 있다.

근데 R(1)=-1 이라고 아까 구했으니까
x=1을 대입해주면
다음과 같은 관계식을 하나 얻는다.

근데 이것만 가지고는 a와 b의 값을 알아낼수 없다.
관계식이 하나 더 필요하다.

이번엔 여기다 x=2를 대입해보자.

R(2) = 6 이다.

여기다가 x=2를 대입하면 관계식을 하나 또 얻는다.

아까 구한 a+b=-1 과 연립하면
a=7, b=-8 이다.
따라서 R(x)는 다음과 같다.

R(x) : 나머지
따라서 이 문제의 답은 7x-8 이다.
- 나머지정리 -
다항식을 일차식으로 나누었을 때의
나머지를 구하는 방법을 나머지정리라 한다.

이런 문제를 풀때 사용되는게 '나머지정리' 인 것이다.
주의할건 '일차식'으로 나누었을때의 나머지를 구하는거다.
일차식으로 나누는것 외에는 나머지정리라 하지 않는다.
아까 저 문제를 풀때 내가 알려준 방법이 바로 나머지정리이다.
아까 저 문제를 어떻게 풀었나?
'항등식'을 세워서 풀었다.
항등식을 세워서 푼다는게 핵심이다.

여기서 몫은 x에 대한 다항식이니 Q(x)라 쓰고
나머지는 상수이니 R이라 쓴다고 했다.

그리고 나머지만 구하면 되기때문에 몫은 필요없다.
따라서 몫 부분을 0으로 만든다.
그러려면 x-1=0 이어야하고
따라서 x=1 이어야 한다.
x=1을 위 식에 대입하면

나머지는 2 임을 알수 있다.
- 일반화 -
이제 이걸 일반화해보자.
다항식을 일차식으로 나누었을 때의
나머지를 구하는 방법을 나머지정리라 한다.
여기서 다항식을 P(x)라 두겠다.
다항식이 영어로 Polynomial 이라 앞글자 따온거고
x에 대한 다항식이니 P(x)라 한것이다.
그리고 나누고자 하는 일차식을
x-α 라 두면
아래와 같은 항등식을 세울수 있다.

여기서 수포자가 많이 생기는 이유가
식에 숫자가 한개도없어서 지레 겁을먹고 포기하는것이다.
근데 좀 이해안되는부분이 있을것이다.
1. 왜 나누고자 하는 일차식을
x+α라 두는게 아니라 x-α 라 두는가?
2. 일차식이 2x-3 이런식이면 x의 계수가 1이 아닌데 어떻게할건가?
하나씩 설명해주겠다.
1. 왜 나누고자 하는 일차식을
x+α라 두는게 아니라 x-α 라 두는가?
x-α라 두면

이 식에서 몫 부분을 0으로 만드는 x값이 얼마인가?
x-α=0 을 만족시키는 값이다.
그런 x값은 α이다.
따라서 여기다 x=α를 대입하면

이렇게 깔끔한 결론을 얻게된다.
그래서 x-α라 두는거다.
요약하자면, 그냥 그게 깔끔하고 편해서.
2. 일차식에서 x의 계수가 1이 아니면 어떻게할까?
만약 나누고자 하는 일차식이 2x-3 이라고 해보자.
그럼 아래와 같이 써진다.

근데 꼭 나누고자 하는 일차식이
x의 계수가 1일 필요가 없다.
여기서 나머지를 구하는 핵심이 되는 논리는
항등식이라 x값을 아무거나 넣어도 성립한다는것이다.
즉 몫 부분을 0으로 만들수만 있다면
사실 일차식의 생김새는 중요하지 않다.
그 일차식의 값이 0이 되도록 하는 x값만 잘 찾아서 넣어주기만 하면 되는것이다.
저 식에서 몫부분이 0이 되려면
2x-3=0 을 만족하는 x값을 대입해야한다.
그런 x값은 3/2 이다.
따라서 x=3/2 를 대입하면 다음과 같은 결론을 얻을수 있다.

요약하자면, 일차식의 생김새는 중요하지 않다.
x-α 라는건 그냥 결론이 가장 깔끔하게 나오는 일차식의 생김새인거고
일차식이 어떻게 생겼든 그 일차식이 0이 되도록 하는 x값만 찾아주면 된다.
아무튼 이제 진짜 일반화하면
다항식 P(x)를 일차식 x-α으로 나누었을 때의
나머지를 구하는 방법을 나머지정리라 한다.
그러면 아래와 같은 항등식을 세울수 있다.

그리고 나머지를 구하기 위해 몫 부분을 0으로 해야하고
그러기 위해 x=α를 대입해보면
다음과 같은 결론을 얻는다.

즉 일차식으로 나눌때는
항등식을 세우는 과정까지도 생략이 가능하다.
- 예제로 중간점검 -

다항식을 일차식으로 나누었을때
나머지를 구하는거니까
나머지정리를 이용해봐야겠다. 라고 추론할수 있다.
일단 항등식을 세우면
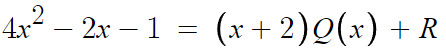
이제 몫 부분을 0으로 만들기 위해
x=-2 를 대입하면
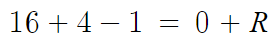
따라서 R=19 이고
따라서 답은 19
아까 나머지정리의 일반화 공식을 이용해 풀수도 있다.
항등식을 세우지 않고 푸는방법이다.

여기서 α = -2 인 것이다.
따라서 R = P(-2) 이고
P(-2) = 19 이므로 답은 19
- 인수정리 -
10은 5로 나누어떨어진다.
왜 나누어떨어진다고 할수 있는가?
10 = 5×2 라서
'나머지가 0'이기 때문이다.
나머지가 0이면 나누어떨어진다고 표현한다.
다항식도 똑같다.
나머지가 0이면 나누어떨어진다고 표현한다.
아까 나머지정리에서 세운 항등식을 떠올려보자.

여기다가 x=α 를 대입하면 나머지 R의 값을 구할수 있다.

근데 나누어떨어진다면?
나머지가 0이라는거니까 R=0 이다.
따라서 아래와 같은 결론을 얻는다.


그리고 가장 중요한 내용
이것의 이름이 인수정리인 이유
P(x)가 x-α 로 나누어떨어진다는건
P(x)를 '인수분해' 하면 'x-α를 인수로 갖는다'는 뜻이다.
예를 들어주겠다.
x²-1 = (x-1)(x+1) 이다.
조금 다르게 표현하면
x²-1 = (x-1)(x+1) + 0 이다.
즉 x²-1 을 x-1로 나누면
몫이 x+1 이고 나머지가 0이다.
즉 x²-1 은 x-1 로 나누어떨어진다.
그리고 x²-1 = (x-1)(x+1) + 0 은
교환법칙에 의해
x²-1 = (x+1)(x-1) + 0 라고 표현할수도 있다.
즉 x²-1 을 x+1로 나누면
몫이 x-1 이고 나머지가 0이다.
따라서 정리하면,
아래 세가지는 같은 말이며,
다항식 P(x)가 x-α로 나누어떨어진다는 뜻이다.

- 예제 -
1 )

- 첫번째 풀이 : 항등식 세워서 풀이 -

몫 부분을 0으로 만들기 위해 x=-3 을 대입하면
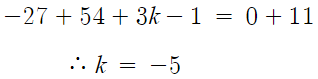
따라서 답은 -5
- 두번째 풀이 : 나머지정리를 이용한 풀이 -
일차식으로 나누었고
그때의 나머지가 언급되었으므로
나머지정리를 이용해보자고 추론해볼수 있다.

여기서는 일차식 x+3 으로 나눴으니
α = -3 이고
따라서 P(-3) = R 이며
R = 11 이므로
P(-3) = 11 이다.
P(-3)을 구하기 위해 P(x)에 x=-3을 대입하여 정리하면

따라서 답은 -5
2 )

핵심 : 나누어떨어진다 = 나머지가 0이다.
따라서 인수정리 문제이다.
따라서 나눗셈에서의 항등식을 세우면
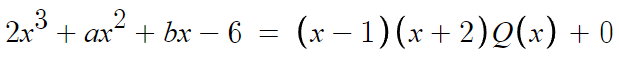
Q(x)를 직접 구한다음 전개해서 계수비교해도 되지만
Q(x)를 구하려면 직접 나눠봐야하기때문에
너무 오래걸리고 실수하기도 쉽다.
최대한 Q(x)를 구하지 않는 방향으로 할거고
그러려면 Q(x)에 상관없이 저 식이 성립하게 하려면
Q(x) 부분을 0으로 만들어야한다.
즉 (x-1)(x+2)=0 을 만족하도록 해야한다.
따라서 x=1 또는 x=-2 를 대입해볼것이다.
x=1 을 대입하면
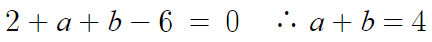
따라서 a+b=4 이다.
x=-2 를 대입하면
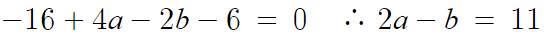
따라서 2a-b=11 이다.
아까 구한 a+b=4 라는 식과 연립하면
a=5, b=-1 임을 알수있다.
따라서 답은 a=5, b=-1
'수학(상) > I. 다항식' 카테고리의 다른 글
| 인수분해 (0) | 2022.01.07 |
|---|---|
| 조립제법 (2) | 2022.01.07 |
| 항등식과 미정계수법 (0) | 2022.01.04 |
| 다항식의 연산 #3 - 다항식의 나눗셈 (0) | 2022.01.04 |
| 다항식의 연산 #2 - 다항식의 곱셈 (0) | 2021.12.29 |



