
- 개요 -
아주 재밌는내용이다.
내가 대단원 시작할때
도형을 수식으로 다루는 방법을 다루는 단원이라 소개했는데
도형을 수식으로 다뤄서 증명하는 정리이기 때문에
고1 도형의 방정식 단원에 이 내용이 들어온것이다.
- 삼각형의 중선정리 -
파푸스의 중선정리 또는 아폴로니오스 정리 라고도 부른다.

삼각형이 있다.
이등변삼각형도 아니고 직각삼각형도 아니고
대충생긴 삼각형이다.
이 중선정리는 아무 삼각형이나 다 성립한다는 뜻이다.
여기서 아무 꼭짓점이나 골라보자.
난 보기편하게 A를 골라보겠다.
점 A에서 선분 BC의 중점에 선을 긋는다.
즉 중선을 긋는다.
중점은 그냥 중간지점이라 보면 된다.

중점을 M이라 하겠다.
M은 BC의 중점이기 때문에
BM의 길이와 CM의 길이가 같다.
그리고 여기서 이것에 관련된 특별한 법칙이 있으니
그걸 삼각형의 중선정리 라고 이름붙인것이다.
그래서 정확히 어떤 법칙이 있냐면

AB의 길이를 a
AC의 길이를 b
BM, CM의 길이를 c
AM의 길이를 d
라고 하면,
아래 식이 성립한다.

이를 삼각형의 중선정리라 한다.
- 증명 -
증명할때 쓰이는 아이디어는 꽤 간단하다.
점과 점 사이의 거리 공식을 이용한다.

우선 이 삼각형을 xy좌표평면에 놓을건데
점 M이 원점에 오도록 놓을것이다.
점 M이 원점에 오도록 놓는 이유는
그래야 식이 간단해진다.

여기서 점 A의 좌표를 (a, b)
점 B의 좌표를 (-c, 0)
점 C의 좌표를 (c, 0)
점 M의 좌표는 원점에 놨으니 (0, 0)
이라 하겠다.

그다음
A와 B 사이의 거리,
A와 C 사이의 거리,
B와 M 사이의 거리,
C와 M 사이의 거리,
A와 M 사이의 거리 를
두 점 사이의 거리 공식을 이용하여 적으면

일단 이렇게 써놓고
우리가 증명해야할 최종적인 식이

이거니까 각각 대입하면

이제 이걸 정리만 해주면 증명이 완료된다.

여기서

AB = a, AC = b, BM = c, AM = d 이므로
이것까지 대입해서 정리하면 정말로 증명 완료

증명을 직접 한번만이라도 해보길 바란다.
식이 좀 길고 복잡할 뿐이지
두 점 사이의 거리 공식만 가지고 푸는거라 어려운건 아니다.
직접 해봐야 안까먹는다.
- 요약 -

증명 방법은, M을 좌표평면의 원점에 놓고
두 점 사이의 거리 공식을 적용하면 된다.
- 예제 -

삼각형 ABC가 있다.
점 M은 선분 BC의 중점이며
선분 AB, BC, AM의 길이는 각각 9, 8, 3√5 이다.
선분 AC의 길이를 구하시오.
삼각형이 있고 중선이 있으므로
삼각형의 중선정리를 이용해봐야겠다 라고 추론할수 있다.
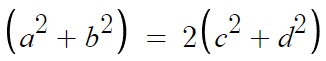
여기서 a=9, c=4, d=3√5 인거고
b의 길이를 저 공식에 대입해서 알아내면 된다.
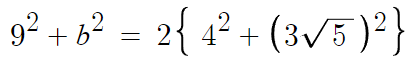
이를 정리하면 b² = 41
b는 선분의 길이니까 양수이다.
따라서 b=√41
따라서 답은 √41
'수학(상) > IV. 도형의 방정식' 카테고리의 다른 글
| 직선의 방정식 #1 - 직선의 방정식 작성 (0) | 2022.03.01 |
|---|---|
| 자취의 방정식 - 점의 자취 (0) | 2022.03.01 |
| 삼각형의 무게중심 (0) | 2022.02.27 |
| 선분의 내분점과 외분점 (0) | 2022.02.24 |
| 두 점 사이의 거리 (0) | 2022.02.20 |



