
- 개요 -
'수학계 3대 떡밥'은
Ⅰ) 0.999... = 1 인가?
Ⅱ) 몬티홀 문제 : 선택을 바꿔야 하는가?
Ⅲ) 정수와 짝수의 개수가 같다고?
이건데, 이것중 첫번째것을 다룰것이다.
독자의 수준을 고려하여 아주 쉽게 설명해줄것이지만,
중3수준의 지식은 갖고있다고 가정하고 진행한다.
결론부터 말하자면,
0.999... = 1 이다.
- 들어가며 : 이것이 왜 떡밥인가? -
사람들이 혼란스러울만 한 주제이다.
이걸 가지고 커뮤니티에서 논쟁이 벌어지는 일이 많다.
아니, 1보다는 아주아주아주 조금이라도 작은 수 아닐까?
아니, 0.9 < 1 이고 0.99 < 1 이고 0.99999 < 1 인데
이런식으로 반복하면 당연히 0.999... < 1 아니냐?
0.999... 는 1에 한없이 다가가는 수이지
결코 1이 될수는 없는거 아니냐?
아니, 0.999... 는 정수부분이 0이고 1은 정수부분이 1인데
그럼 0.999... < 1 아니냐?
이런식으로 말이다.
위의 논리는 다 그럴싸하지만 틀린말이다.
왜 이런 혼란이 생겼는지 알아보자.
- 1 : 무한에 대한 오개념 -
0.999... 는
0에서 소수점 아래로 9가 무한히 늘어서는 수이다.
즉 '무한소수'이다.
0.999...가 무한소수인데
무한이라는것 자체에 오해가 있어서 이런 혼란이 생긴것이다.
'무한' 이라는건
말 그대로 '한계가 없다' 라는 '표현'이다.
즉 무한하다는건 끝이 없다는거다.
0.999... 는 9가 끝없이 계속 늘어서는 수이다.
이걸로 위에 보여줬던 4개의 잘못된 논리중 두번째것이 반박된다.
아니, 0.9 < 1 이고 0.99 < 1 이고 0.99999 < 1 인데
이런식으로 반복하면 당연히 0.999... < 1 아니냐?
이건 어떤 오류를 범하고 있는거냐면
0.9, 0.99, 0.99999 는 다 끝이 있는 수이다.
근데 0.999... 는 끝이 없이 9가 계속 늘어서는 수이다.
맘대로 0.999... = 0.999...9 라고 하면 반칙이다.
끝이 없다니까? 누구 맘대로 소수를 끝내나?
0.999... 를 0.999...9 라고 써버리는 순간
얘는 '유한소수'가 되어버리는데?
그래서 저건 틀린 논리인것이다.
여기서 재반박이 들어올수가 있다.
Q) 그래도 끝자리가 9인건 맞잖아요?
끝자리가 9인건 맞는데, 그래서 끝자리가 어디인가? 끝이 없다니까?
다시 말하지만 0.999...9는 맘대로 소수를 끝내버린거다.
0.999... 는 무한소수이고, 0.999...9는 유한소수이기 때문에
0.999... ≠ 0.999...9 이다.
따라서 0.999...9 < 1 이라는것은
0.999... < 1 이라는 주장의 근거로 사용될 수 없다.
추가로, 1 - 0.999... = 0.000...1 이므로
0.999...≠1 이다. 라고 주장하는 사람도 있는데
이것도 같은 맥락으로 반박이 된다.
0.000...1 은 맘대로 소수를 끝내버린거니까 반칙이다.
- 2 : 수와 극한이라는 개념에 대한 오해 -
이번건 위에 보여줬던것중 세번째 논리에 대한 반박이다.
0.999... 는 1에 한없이 다가가는 수이지
결코 1이 될수는 없는거 아니냐?
이런 논리를 전개하는건, 수 라는 개념 자체를 오해하고 있는것이다.
수는 절대 움직이지 않는다.
'가까워지는 상태'에 있는 수는 존재하지 않는다.
0.9 뒤에 9를 계속해서 붙이면 점점 1에 가까워지긴 한다.
근데 이걸 오해해서 논리를 잘못 적용한거다.
3 이라는 수로 예를 들어보겠다.
3 이라는 수는 값이 변하는가?
절대로 변하지 않는다.
3 이라는 수는 움직이지 않는다.
그래서 3을 상수라고 부르는거다. constant number
0.999... 도 상수다. 얘가 변수는 아니잖아요?
0.999... 라는 수는 절대로 값이 변하지 않는다.
얘가 1에 '가까워진다' 라는 표현 자체를 쓸수 없다.
수는 절대로 움직이지 않기 때문이다.
그럼 혹시 변수는 움직일수 있는 수인가?
그건 또 아니다. 변수의 뜻 중 '변할수 있는 수' 라는건
값이 움직인다는게 아니라,
어떤 값이 들어갈 '자리'가 있는데, 그 자리에 들어갈 값을 정확히 뭔지 몰라서
임의로 x, a 이런식으로 적어놓은거다.
수가 움직인다는 오개념은 보통 어디서 생기냐면
고등학교에서 '극한'을 배울때 생긴다.

얘를 보고
아 x가 3을 향해서 가니까 극한값은 3인거구나
라고 이해했기 때문에 이런 오개념이 생긴거다.
x를 두고 3에 가깝게 붙인다는게 아니라,
변수 x의 값을 정할건데, 그 값을 3에 가깝게 할거라는 뜻이다.
그니까 변수 x의 값을 정할건데 3에 아주 가까운 지점으로 할거라는 말이다.
근데 이건 이런 오개념이 생기기 쉬운게
극한 이라는 개념 자체가 원래 상당히 어려워서
고등수학에서는 그냥 x가 3을 향해서 간다 라고 설명하는게
직관적으로 이해가 쉽기때문에 고등학교에서는 그렇게 설명하는거다.
그래서 왜 틀렸는진 알겠고 이제 증명할 시간이다.
- 증명 1 : 1/3을 이용한 증명 -
가장 쉬운 증명법이다.
아래로 갈수록 어려운 증명법이다.

- 증명 2 : 무한소수를 분수로 나타내기 -

여기서 질문이 있을수 있다.
9.999... - 0.999... 의 결과값은
10x 구할때 9가 한자리씩 밀렸으니 9.000...1 일텐데
0.000...1 은 어디로 갔나요?
벌써 세번째 말하는건데 맘대로 소수를 끝내지 마라.
9.999... 든 0.999... 든 9가 끝없이 늘어져있는 수라는건 변하지 않는다.
9의 끝이 없다. 그래서 100x를 하든 100000x를 하든 무조건 계속 9가 계속 늘어져있는 수가 되는거고
한자리가 밀리든 100자리가 밀리든 9는 끝없이 나온다.
그래서 10x와 x를 빼면 소수점 아래는 다 날아가고 9만 남는것이다.
사실 위의 두가지 증명법은 엄밀히 따지면 완벽한 증명은 아닌데,
그걸 여기다 설명하면 너무 어려워지니 일단 여기서는 패스한다.
궁금하면 아래로 내려가보자.
- 증명 3 : 나눗셈 증명법 -
이건 증명이라 하기는 좀 그런게
인터넷 어딘가에서 봤던거라 사실확인이 안된다.
그냥 재미로 보자.
9 나누기 9 는? 당연히 1이다.
근데 이걸 1을 안쓰고 계산하려 해보자.

이처럼 9가 끝없이 늘어서게 되고,
그래서 0.999... = 1 이다.
- 증명 4 : 귀류법 -
아니, 0.999... 는 정수부분이 0이고 1은 정수부분이 1인데
그럼 0.999... < 1 아니냐?
이걸 반박하는 증명법이다.
0.999... ≠ 1 이라고 가정하겠다.
이렇게 가정하고 논리를 전개하다가, 논리적인 오류가 발견되면
이건 틀린 가정이 되는것이다.
0.999... ≠ 1 이라면
0.999... < 1 이거나
0.999... > 1 이다.
일단 0.999... 의 정수부분은 0이기 때문에
0.999... > 1 은 확실히 틀렸다.
그럼 0.999... < 1 이어야 하는데,
0.999... < 1 이려면
실수는 연속적이기 때문에,
0.999... 와 1 사이에 실수가 존재해야한다.(실수의 조밀성)
즉 0.999... < x < 1 을 만족하는 x가 존재해야한다.
하지만 이런 x는 존재할수 없다.
1보다 작으면서,
소숫점 아래로 9가 끝없이 나오는 수보다 큰 수 x를 찾을수 없다.
따라서 0.999... ≠ 1 이라는 가정은 틀렸다.
따라서 0.999... = 1 이다.
여기서 반박이 들어올 수 있다.
0.999... 보다 큰 수를 찾고싶으면
0.999...의 끝에다가 1만 붙이면 되는거 아닌가요?
그니까 0.999...1 이면 0.999...보다 크잖아요 그럼 되는거아닌가요?
이건 처음에 무한에 대한 오개념 부분에서 설명한 내용이다.
0.999...1 은 반칙이다. 누구 맘대로 소수를 끝내나?
애초에 끝이 없이 9가 계속 늘어서는데 1을 끝에다가 어떻게 붙일건가?
말도 안되는 소리이다.
- 증명 5 : 등비급수 -
여기부턴 이과내용이다.
수열의 극한을 이용할것이다.
수열 a_n을 아래와 같이 둔다.

이러면 0.999... 를 등비급수로 표현할 수 있다.

따라서 0.999... 는
첫째항이 0.9 이고 공비가 1/10 인 등비수열의
등비급수의 합을 의미한다.
그 값을 구해보면, 아래와 같다.

따라서 0.999... = 1 이다.
- 증명 6 : 엡실론-델타(ε-δ) 논법 (가장 엄밀한 증명) -
여기는 고등학교수준이 아니며, 아주 어렵기때문에
고등학생이면 그냥 뒤로가기 눌러도 된다.

내가 0.999... = x 라 두고 10x - x 로 하는 이 증명법이
완벽하지 않다고 한 이유는,

내가 저기서 0.999... 라는 등비급수가 x에 수렴한다고 가정하고 진행한거다.
이걸 하기전에, 0.999... 라는 수가 수렴함을 먼저 보여야한다.
즉, 첫줄부터 증명해야한다.
이는 엡실론-델타(ε-δ) 논법으로 증명할수 있다.
우선 a_n을 새로 정의한다.
a₁=0.9, a₂=0.99, a₃=0.999, ... 로 정의되는 수열 a_n이 있을 때,
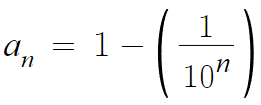
0.999... 라는 수는 이 수열의 항중 하나이므로
이 수열 a_n이 위로 유계(실수인 상계를 가짐)인 단조수열임을 보이면 된다.
우선 a_n은 자명하게 상계를 갖는다.
10은 임의의 a_n보다 무조건 크거나 같기때문이다.
그리고 a₁≤a₂≤a₃≤...≤a_n≤... 이므로 a_n은 단조증가수열이다.
유계인 단조증가수열이므로 수렴한다.
이는 실수의 완비성(Dedekind의 절단공리)으로 증명 가능하다.
여기서 상계가 아닌 실수의 집합을 A라 하고, x를 A의 원소라 하면,
x는 이 수열의 상계가 아니므로 이 수열에는 x < a_m 을 만족하는 수 a_m이 존재한다.
그리고, x와 a_m 사이의 수는 모두 상계가 아니므로, 집합 A의 원소이다.
따라서 A에서는 최대수가 없다.
따라서 상계인 실수의 집합을 A'이라 하면 A'엔 최소수가 존재한다.
왜냐면 (A, A')은 실수전체집합을 절단한거기 때문에,
A에서 최대수가 결정되거나 A'에서 최소수가 결정되어야한다.
이 최소수를 α라 하겠다.
그러면 임의의 양수 ε에 대하여 0 < α-x < ε 를 만족하는 A의 원소 x가 존재하고,
또한 이 x에 대하여 x < a_p인 수 a_p가 존재한다.
여기서, N=p 라 할 때, n≥N 이면 a_N ≤ a_n ≤ α 이므로 0 < α-a_n < α-x < ε 이고,
따라서 임의의 양수 ε에 대하여, 0 < α - a_n < ε 를 만족하는 a_n이 존재한다.
따라서 a_n은 α에 수렴한다.
이제 수렴값이 1(상한이 1)임을 증명하면 된다.
이것도 엡실론-델타(ε-δ) 논법으로 증명할수 있다.
임의의 양수 ε 이 있다고 해보자. n→∞ 일때, | a_n - 1 | < ε 임을 보이면,
a_n의 극한값과 1의 차이는 모든 양수보다 작다는 뜻이므로
a_n의 극한값이 1임이 증명완료된다.
a_n = 1 - (1 / 10ⁿ) 이다.
따라서 임의의 양수 ε에 대하여 양수 δ을 δ > 1/10ε 로 잡으면,
n≥δ 이므로 n ≥ δ > 1/10ε 이다.
따라서 ε > 1/10n
따라서, | a_n - 1 | = ( 1 / 10ⁿ ) ≤ ( 1 / 10n ) < ε
따라서 a_n의 극한값은 1이며, 0.999... = 1 이다.
Q. E. D.
- 그래도 찝찝하다 -
증명은 됐고, 다 알겠는데
그래도 뭔가 받아들여지지 않는 느낌이다.
일단 내가 봐도 그렇고, 수학적으로 반박할수는 없는데
그렇다고 직관적으로 이해가 되지는 않는다.
그냥 1+1을 2라고 약속한것처럼, 이것도 그냥 그런거라고 받아들이자.
모든 것은 0.999... 가 끝이 있는 소수라는 오개념에서 시작된거니까
그것만 바로잡았다면 충분하다.
그리고 추가로,
0.999...와 1이 오차가 있긴 하지만 아주 작기때문에
그냥 편의상 0.999...=1 로 쓰겠다.
라는말은 틀린말이니까 주의하자.
그냥 완전히 똑같은거다. 1+1=2 랑 다를바 없다.
'상식 한접시 > 수학상식' 카테고리의 다른 글
| 수학계 3대 떡밥 #2 - 몬티홀 문제: 선택을 바꿔야 하는가? (0) | 2022.05.01 |
|---|
