
- 개요 -
이번엔 명제의 표현법중 하나인 'p→q'와
이에 관련된 수학용어인 '명제의 역과 대우' 에 대해 배울것이다.
- 명제 p→q 란 무엇인가? -
두 조건 p, q에 대해서
'p이면 q이다.'
라는 명제를 기호로
p→q 라고 표현한다.
여기서 p를 이 명제의 '가정' 이라 하고,
q를 이 명제의 '결론' 이라 한다.
즉, p라 가정하면 결론적으로 q인가?
라는걸 묻는거다.
명제이기 때문에, 이건 참일수도 있고 거짓일수도 있다.
그리고, 오개념에 주의해야한다.
'결론' 이라는 애매한 용어때문에 여기서 오개념이 잡힐 수 있다.
'결론' 이라는건 조건 q 말하는거지
명제의 참 거짓을 말하는게 아니다.
예를 들어, p→q 라는 명제의 결론을 말하라하면
그냥 조건 q 라고 하면 되는거다.
참입니다 거짓입니다 하면 안되는것이다.
- 명제 p→q 의 참, 거짓 -
그래서 이것의 참, 거짓은 어떻게 판별하는가?
수학적 표현은 어렵게 되어있지만, 사실 아주 간단하다.
'p이면 q인가?' 라는것의 참 거짓을 판별하면 된다.
일단 예시를 들어서 이해시켜준다음,
수학적 표현으로 확장하겠다.
p: x는 자연수, q: x는 정수
라고 하면,
명제 p→q 는 참인가?
그니까, '자연수이면 정수인가?'
답은 '참'이다.
모든 자연수는 정수이기 때문이다.
따라서, 자연수이면 정수이고 저 명제는 참이다.
이게 수학적으로 왜 참이냐면,
p에 해당되는 x값을 아무거나 들고와도
그 x값은 q에 해당된다는거다.
자연수 아무거나 들고와도 다 정수일거 아닌가?
그래서 p이면 q이다. 라는 명제가 참이 되는것이다.
q가 p 전체를 포괄하고있기 때문이다.
p: x는 소수, q: x는 홀수
라고 하면,
명제 p→q 는 참인가?
그니까, '소수이면 홀수인가?'
답은 '거짓' 이다.
왜냐면, 2는 짝수인데 소수이기 때문이다.
이게 수학적으로 왜 거짓이냐면,
만약 p→q 가 참이라면
p에 해당되는 x값을 아무거나 들고와도
그 x값은 q에 해당되어야한다.
근데 그렇지 않다. x가 2면?
2는 소수이므로 p를 만족하는데
2는 홀수가 아니므로 q는 만족하지 않는다.
q가 p 전체를 포괄하고있지 못한다는 뜻이다.
그래서 이럴때 p→q 는 거짓이 되는것이다.
추가로, 방금 예시로 들었던 x=2 처럼
어떤 명제가 거짓이 되는 예시를
명제의 '반례' 라 한다.
즉, 어떤 명제가 거짓임을 증명해보이고 싶다면
반례를 찾는것이 하나의 방법이다.
여기선 명제 p→q 가 거짓임을 증명하기 위해
p는 만족하지만 q는 만족하지 않는 예시인 x=2 를
명제 p→q 의 반례로써 사용한 것이다.
이제 이걸 수학적으로 표현해보자.
명제 p→q 가 참이다?
q가 p를 포괄하고있다
즉 q가 p를 담고있다는 뜻이다.
따라서, 조건 p의 진리집합을 P
조건 q의 진리집합을 Q 라고 하면,
P는 Q의 부분집합이다.
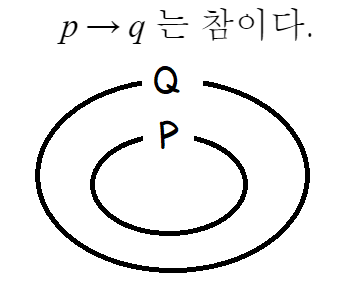
명제 p→q 가 거짓이다?
q가 p를 포괄하고있지 않다는 뜻이다.
따라서, 조건 p의 진리집합을 P
조건 q의 진리집합을 Q 라고 하면,
P는 Q의 부분집합이 아니다.
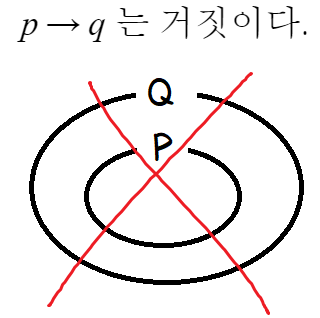
이걸 정리하면,

역도 성립한다는게 무슨말이냐면, 바로 다음에 다룰 내용인데
p→q가 참이면 P⊂Q 이다. 라는것도 성립한다는 말이다.
- 명제의 역과 대우 -
명제 p→q 에 대한 내용이다.
가정은 p이고, 결론은 q이다.
여기서, 가정과 결론의 자리를 바꾼걸
명제의 '역'이라 한다.
즉, p→q 의 역은 q→p 이다.
'명제의 역' 도 명제이다.
조심할것은,
어떤 명제가 참이라고 그것의 역이 항상 참이라는 보장은 없으며,
어떤 명제가 거짓이라고 그것의 역이 항상 거짓이라는 보장 또한 없다.
p→q 가 참이라는건
p, q에 대한 진리집합 P, Q에 대해
아래의 벤다이어그램으로 그려진다는거다.

따라서, p→q 가 참이라고
q→p 가 참인것은 아니다.
아까 말했던 p→q 참거짓 판별에서
그 역도 성립한다. 라고 적어놓은 이유가 그거다.
어떤 명제가 참이라고 그 명제의 역까지 참이라는 보장은 없지만,
참인 경우도 당연히 있고, 방금은 그런 경우였다.
여기서, 가정과 결론을 각각 부정하여
서로 자리를 바꾼걸 명제의 '대우' 라고 한다.
가정은 p이므로, 가정의 부정은 ~p 이고
결론은 q이므로, 결론의 부정은 ~q 이다.
따라서, p→q 의 대우는 ~q→~p 이다.
'명제의 대우'도 명제이다.
대우는 중요한게,
어떤 명제가 참이면, 그것의 대우도 무조건 참이다.
어떤 명제가 거짓이면, 그것의 대우도 무조건 거짓이다.
p→q 가 참인 경우의 벤다이어그램을 그려보면

이렇게 된다는거고
p→q 의 대우는 ~q→~p 이다.
~q→~p 라는건, 'q가 아니면 p도 아니다.'
라는 뜻이다.
벤다이어그램으로 봤을 때, q가 p를 담고있는데,
q가 아니면 p도 아닐수밖에 없다는걸 볼 수 있다.
대우는 그래서 왜 배우냐면,
어떤 명제의 참 거짓 여부를 판단할 때,
그 명제를 가지고 판단하는것보다
그 명제의 대우의 참 거짓을 판단하는게 더 쉬울 때가 있다.
대우가 참이면 명제도 참이니까 대우의 참 거짓만 판단해도 된다.
예시를 들어주겠다.
'x²≠4 이면, x≠2 이다.' 라는 명제의 참 거짓을 판별해보자.
p: x²≠4 , q: x≠2
라고 하면, 위의 명제를
'p이면, q이다.' 즉, p→q 라고 표현할수 있다.
이것보다 대우의 참 거짓을 판단하는게 더 쉽다.
p→q 의 대우는 ~q→~p 이고,
~q: x=2 , ~p: x²=4
따라서, 'x=2이면, x²=4이다.'
라는 명제가 만들어진다.
이 명제는 참임을 쉽게 판단할 수 있다.
대우가 참이므로, 이 명제는 참이다.
1 )

가정 : ab=0 이다.
결론 : a=0 또는 b=0 이다.
ab=0 이라는건, a나 b 둘중 하나는 0이라는거다.
따라서, ab=0 이려면 a=0 또는 b=0 이어야한다.
따라서 이 명제는 참이다.
2 )

p→q 가 거짓이라는건
Q가 P를 다 포괄하지 못한다는 뜻이다.
즉, p인데 q는 아닌 경우가 존재한다는거고,
그런 원소가 어떤 집합에 속하는지 찾으라는 문제이다.
P인데, Q는 아닌 경우?
그건바로 'P'와 'Q의 여집합' 의 '교집합' 이다.
따라서 답은 4번이다.
3 )

1 )
p→q 가 참이라는건
Q가 P를 담고있다는 뜻이므로
P⊂Q 가 된다. 따라서 1(x)
2 )
이 명제의 역이 q→p 인건 맞는데,
어떤 명제가 참이라고 그것의 역도 참이라는 보장은 없다.
아까 벤다이어그램 그리면서 설명해줬던 내용이다.
따라서 2(x)
3 )
이 명제의 대우는 가정과 결론을 부정한 뒤, 자리를 바꾼것이다.
따라서 이 명제의 대우는 ~q→~p 이다.
어떤 명제가 참이면, 그것의 대우도 무조건 참이다.
이것도 아까 벤다이어그램 그리면서 설명해줬다.
따라서 3(o)
4 )
p를 가정이라 하는건 맞는데,
'참'은 결론이 아니다.
아까 오개념주의하라고 다뤘던내용이다.
결론은 그냥 조건 q 이지
명제의 참 거짓을 판단하라는게 아니다.
따라서 4(x)
5 )
p→q 가 참이라는건
이 명제의 반례가 존재하지 않았다는 뜻이다.
반례가 하나라도 존재하면 거짓이다.
따라서, 5(x)
따라서 답은 3번
'수학(하) > I. 집합과 명제' 카테고리의 다른 글
| 명제 #5 - 절대부등식 (산술평균과 기하평균) (0) | 2022.05.25 |
|---|---|
| 명제 #4 - '모든'과 '어떤', 충분조건과 필요조건, 수학적 증명법 (0) | 2022.05.19 |
| 명제 #2 - 조건과 진리집합, 부정 (0) | 2022.05.07 |
| 명제 #1 - 명제란 무엇인가? (0) | 2022.04.28 |
| 집합 #5 - 집합의 연산 (0) | 2022.04.15 |



