
- 개요 -
많이들 무서워하는 절댓값이다.
이것의 그래프를 그리는 법을 배울것이다.
'수능 킬러문제'에서 자주 나오는 소재이니 꼭 알아둬야하고,
이때 확실히 알고가지 않으면 고3때 고생한다.
- 절댓값 기호가 포함된 식 소개 -

절댓값이 포함된 식은 위의 4가지정도가 있는데,
4개 전부 다 '그래프'를 그려볼것이다.
여기다가 절댓값을 더 씌운다거나 할 수 있는데,
어차피 원리는 똑같아서 이것만 할줄알면 다 그릴 수 있다.
공통적으로 적용되는 기본 원리 : 절댓값 기호는 벗긴다.
- 절댓값 1 -


절댓값 기호는 벗긴다.
절댓값 기호를 벗기는법 : 절댓값기호 안쪽에 있는것의 '부호'가 어떻게 되는가?
만약 음수이면, 절댓값 기호를 벗기기 위해 마이너스(-)를 붙인다.
음수가 아니면 그대로 절댓값 기호만 벗겨주면 된다.

이제 그래프를 그려보자.
일단 f(x)≥0 일때는 무리가 없을것이다.
그냥 f(x)이기 때문이다.
따라서, f(x)≥0 인 부분만 그려보면

이렇게 그려질것이다.
이제 f(x)<0 일때를 그려보자.

f(x)<0 이면 y=-f(x) 이다.
이는 y=f(x)의 그래프를 x축에 대해 대칭이동한것이다.

따라서, y=-f(x) 의 그래프를 그릴거면
y=f(x) 의 그래프를 그대로 x축대칭해서 x축 위로 접어올리면 된다.


이러면 이제 f(x)≥0 인 경우와 f(x)<0 인 경우를 둘 다 그렸으니
y=|f(x)| 의 그래프 그리기가 끝난거다.
따라서, y=|f(x)| 의 그래프는 아래와 같다.

- 절댓값 2 -


절댓값 기호는 벗긴다.
절댓값 기호를 벗기는법 : 절댓값기호 안쪽에 있는것의 '부호'가 어떻게 되는가?
만약 음수이면, 절댓값 기호를 벗기기 위해 마이너스(-)를 붙인다.
음수가 아니면 그대로 절댓값 기호만 벗겨주면 된다.

이제 그래프를 그려보자.
일단 x≥0 일때는 무리가 없을것이다.
그냥 f(x)이기 때문이다.
따라서, x≥0 인 부분만 그려보면

이제 x<0 일때를 그려보자.

x<0 이면 y=f(-x) 이다.
이는 y=f(x)의 그래프를 y축에 대해 대칭이동한것이다.

따라서, y=f(-x) 의 그래프를 그릴거면
y=f(x) 의 그래프를 그대로 y축대칭해서 y축 왼쪽으로 접으면 된다.


이러면 이제 f(x)≥0 인 경우와 f(x)<0 인 경우를 둘 다 그렸으니
y=|f(x)| 의 그래프 그리기가 끝난거다.
따라서, y=|f(x)| 의 그래프는 아래와 같다.

- 절댓값 3 -


절댓값 기호는 벗긴다.
절댓값 기호를 벗기는법 : 절댓값기호 안쪽에 있는것의 '부호'가 어떻게 되는가?
만약 음수이면, 절댓값 기호를 벗기기 위해 마이너스(-)를 붙인다.
음수가 아니면 그대로 절댓값 기호만 벗겨주면 된다.

이제 그래프를 그려보자.
일단 y≥0 일때는 무리가 없을것이다.
그냥 y=f(x)이기 때문이다.
따라서, y≥0 인 부분만 그려보면

이제 y<0 일때를 그려보자.

y<0 이면 y=-f(x) 이다.
이는 y=f(x)의 그래프를 y축에 대해 대칭이동한것이다.

단, 여기서는 조심해야 할 것이
우리가 그릴게 |y|=f(x) 이기 때문에, f(x)<0 인 부분은 그리면 안된다.
절댓값은 절대 음수가 될수 없기때문이다.
따라서, f(x)<0 인 부분은 아예 그리지 않고 놔둔다.

그럼 이제 어떻게 해야하냐?

y<0 인 곳, 즉 x축 아래에다가는
y<0일때 y=-f(x) 이므로,
f(x)를 x축 대칭이동 한 그래프를 그려주면 된다.


이러면 이제 y≥0 인 경우와 y<0 인 경우를 둘 다 그렸으니
|y|=f(x) 의 그래프 그리기가 끝난거다.
따라서, |y|=f(x) 의 그래프는 아래와 같다.

x값 하나에서 y값이 두개 나오며,
심지어 y값 하나에서도 x값이 두개 나오므로
x와 y는 함수관계가 아니라는것에 주의하자.
- 절댓값 4 -

슬슬 막나가는 느낌인데, 여태 잘 따라왔다면 그리 어렵지 않다.

절댓값 기호는 벗긴다.
절댓값 기호를 벗기는법 : 절댓값기호 안쪽에 있는것의 '부호'가 어떻게 되는가?
만약 음수이면, 절댓값 기호를 벗기기 위해 마이너스(-)를 붙인다.
음수가 아니면 그대로 절댓값 기호만 벗겨주면 된다.

그런데 이건 좀 곤란한게, 절댓값 기호가 두개나 있기 때문에
x의 부호에 따라, y의 부호에 따라
경우를 4가지로 나눠야한다. 이건 너무 복잡하다.
그래서 어떻게 할거냐면, '치환'할것이다.

t≥0 이라는 조건은, |x|=t 이니까 생긴거다.
이런식으로 치환할때 범위를 설정해주는게 아주 중요하다.
일단 이걸로 생각하고, 치환한건 나중에 또 처리하면 된다.
'4가지 경우를 한 번에' 처리할것이냐,
'2가지 경우씩 두 번에 걸쳐서' 처리할것이냐 의 차이이다.
당연히 후자가 더 쉽다.
이제 그래프를 그려보자.

그냥 |y|=f(t)이기 때문에, 아까 절댓값3 에서 다룬거랑 똑같다.
다만 여기선 t≥0 이므로, t≥0 인 곳에서만 그린다.
따라서, t≥0 인 부분을 그려보면

이제 치환한걸 다시 돌려줄시간이다.


x≥0 인건 이미 그렸으니, x<0 인것만 하면 된다.
x<0 이면, t=-x 이다.
이는 y=f(x)의 그래프를 y축에 대해 대칭이동한것이다.


따라서 x<0 인것도 그리기 위해,
방금 그린 위의 그래프를 y축 대칭이동해야한다.

이러면 이제 x≥0 인 경우와 x<0 인 경우를 둘 다 그렸으니
|y|=f(|x|) 의 그래프 그리기가 끝난거다.
따라서, |y|=f(|x|) 의 그래프는 아래와 같다.

이것도 x값 하나에 y값 두개씩 나오니
이것 또한 x와 y의 함수관계같은건 없다는걸 유념하자.
이건 여담인데, 이런 식은 수능에 잘 출제되지는 않는다.
함수가 아니기 때문에, 딱히 출제할 껀덕지가 없는것이다.
그래도 출제 안된단 보장은 없으니 당연히 연습해놔야한다.
- 예제 -
1 )

절댓값 기호가 두 개나 있어서 너무 복잡하다.
따라서, 치환해서 풀것이다.
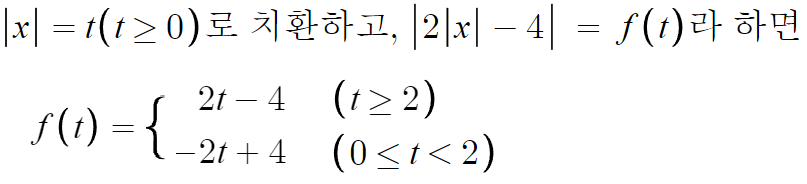
이러면 그나마 간단해진다.
치환한 t는 나중에 |x|로 돌려주면 된다.
저것의 그래프는 할만하다.
t≥2 인곳에서는 2t-4 이고
0≤t<2 인곳에서는 -2t+4 이다.
이걸 그려주면
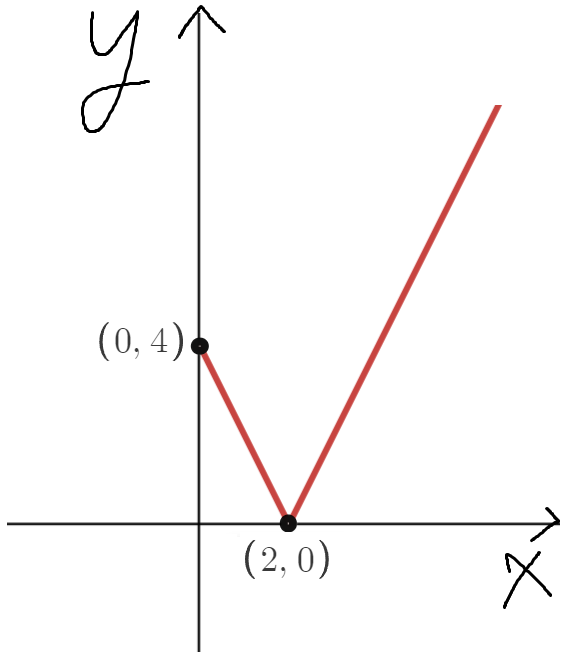
이제 치환한걸 다시 돌려줄시간이다.
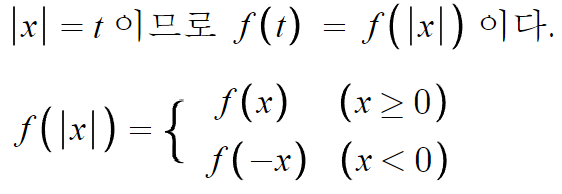
x≥0 인건 아까 이미 그려놨다.

따라서, x<0 인곳만 그리면 되는데,
x<0 인곳에서 f(x) = f(-x) 이므로
x<0 에서 그리고싶다면, 저 그래프를 y축기준 대칭이동시키면 된다.

이게 정답이며, (-2, 0), (2, 0), (0, 4)를 지나는 직선모양 그래프면서
y축, x축과 만날때 저렇게 뾰족하게 꺾여야 정답으로 인정한다.
2 )

이 문제는, 이게 대채 뭘 묻겠다는건지 감을 못잡을수 있는데,
y=|f(x)|의 그래프를 그려보면 느낌이 온다.
일단 f(x)는 최고차항의 계수가 양수인 이차함수이므로
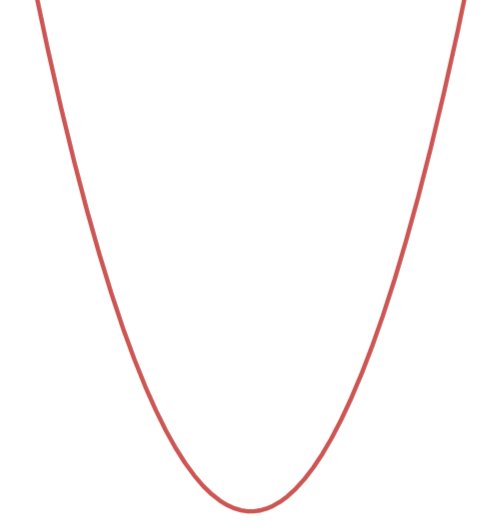
y=f(x)의 개형은 대략 이렇게 될것이다.
x축이 어디있는지는 모르겠으나,
만약 꼭짓점보다 x축이 아래에 있다고 해보자.
해보면 문제상황에 모순이 생긴다는걸 알 수 있다.
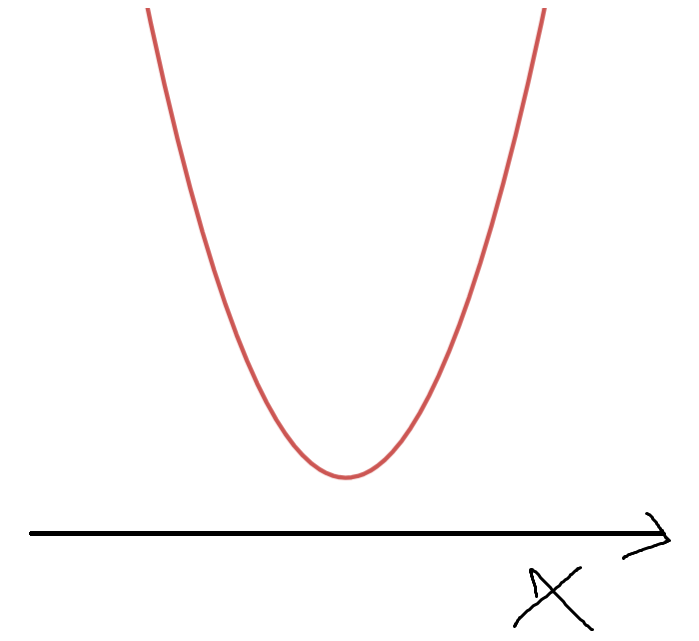
이땐 f(x)가 항상 양수이므로, |f(x)| = f(x) 이다.
그러면 문제 상황에 모순이 생긴다.
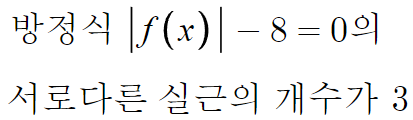
이 조건에 의하면, f(x)-8=0 의 실근이 3개가 나와야한다.
그런데 f(x) 는 이차함수이므로, 절대 실근이 3개 나올수 없다.
따라서 f(x)의 그래프가 x축 위에만 있는것은 불가능하다.
그럼 다음으로, y=f(x)가 x축에 접하는 경우
이것도 아까와 똑같은 논리로,
|f(x)| = f(x) 이므로 절대 f(x)-8=0 의 실근이 3개 나올수 없다.
따라서, f(x)의 꼭짓점은 x축 아래에 있다.
y축이 어디있는지는 정확히 모르겠으나,
일단 아는대로 그려두고 가자.
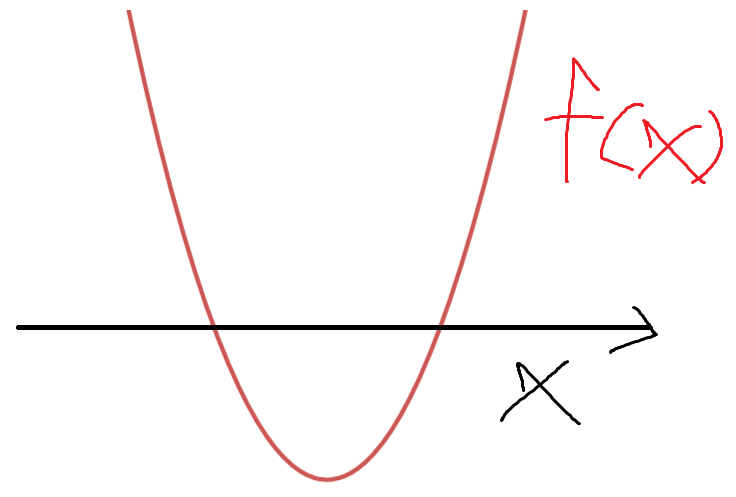
이제 우리가 배운대로 y=|f(x)|의 그래프를 그리자.
f(x)<0 인 곳에서는 f(x)를 x축 대칭이동시키면 된다.
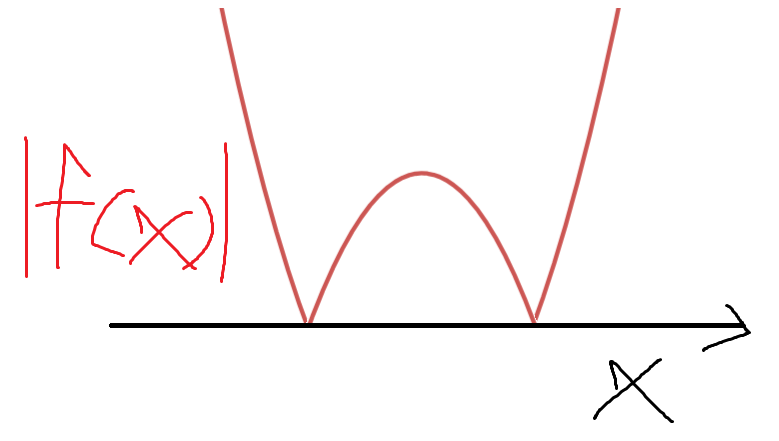
이게 y=|f(x)|의 그래프이다.
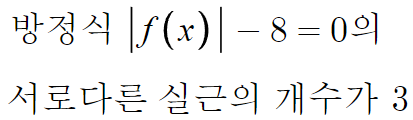
문제에서 묻는 |f(x)|-8=0 의 실근은
곧 |f(x)|=8 의 실근을 묻는거고,
이는, y=|f(x)|의 그래프와 y=8 의 그래프가
세 점에서 만난다는 뜻이다.
왜냐면, 교점이 생긴다는건 '함숫값이 같다'라는 뜻이기 때문이다.

그럼 이것과 y=8이 세 번 만나도록 적절히 y=8 의 위치를 찾아야하는데,
해 보면 알텐데 세번 만나도록 하는 위치는 딱 하나밖에 없다.
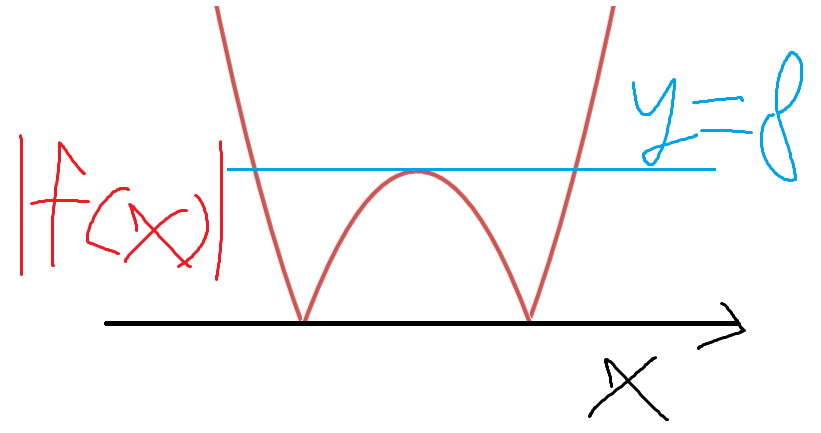
바로 저기 파란선 그은곳이 8 이어야만 |f(x)|와 접하면서 딱 세번 만날 수 있다.
따라서, 이런 결론을 얻는다.
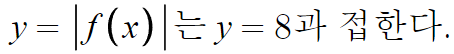
근데 접하는 지점은 f(x)<0 이라서 접어올린곳이다.
따라서, 원래 f(x)의 함숫값은 -8 이다.
따라서, 이런 결론을 얻는다.
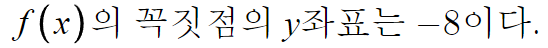
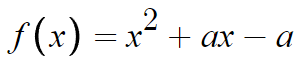
꼭짓점은 수학(상)의 내용으로 어렵지 않게 찾을 수 있다.
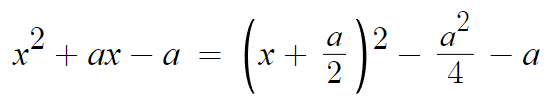
따라서 꼭짓점은 ( -a/2, -a²/4 - a ) 이다.

따라서 답은 4
'수학(하) > II. 함수' 카테고리의 다른 글
| 함수 #10 - 역함수의 그래프 (0) | 2022.08.08 |
|---|---|
| 함수 #8 - 함수의 대칭성 (0) | 2022.07.24 |
| 함수 #7 - 역함수의 정의 (0) | 2022.07.17 |
| 함수 #6 - 합성함수 (0) | 2022.07.10 |
| 함수 #5 - 무리함수 (0) | 2022.07.07 |



