
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 17번으로 가고싶으면 17 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
16 )


따라서 답은 2
17 )


따라서 답은 11
18 )

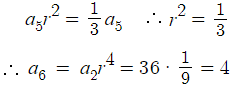
따라서 답은 4
19 )


따라서 답은 6
20 )


따라서 답은 3+5 = 8
21 )


따라서 답은 24
22 )

일단 (가) 조건을 만족하는 삼차함수 f(x)의 개형을 그려보자.
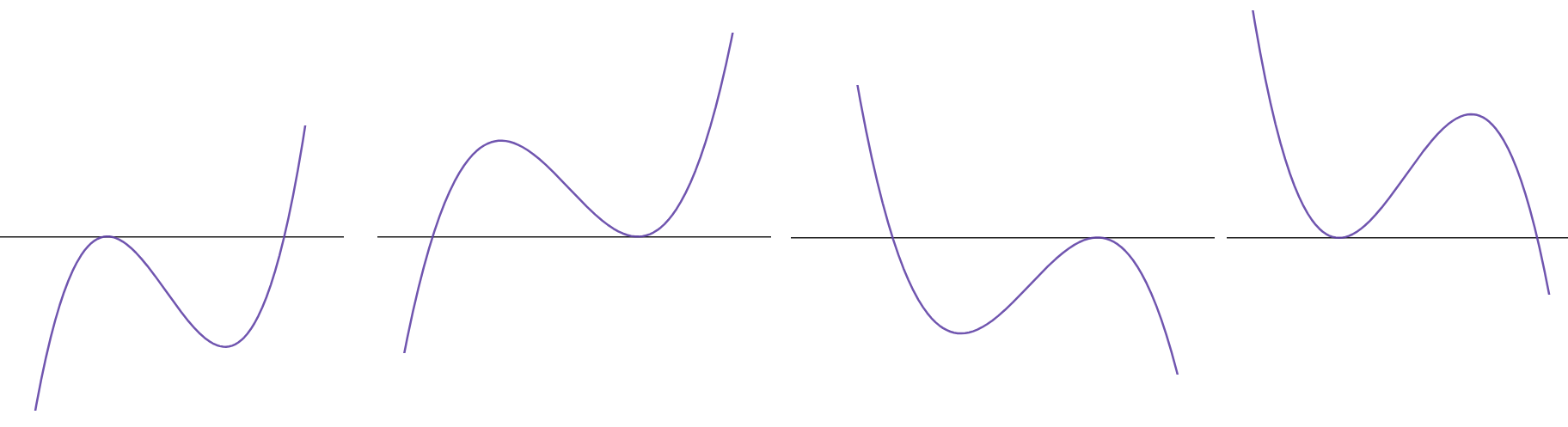
가능한건 이 4개밖에 없다.
여기서 근을
작은걸 α, 큰걸 β 로 놓고
이중 조건에 맞지 않는걸 걸러낼것이다.
(나) 조건 풀이

이제 저걸 저 조건이 만족하는지 왼쪽부터 하나씩 해보자.
1.

만나는 점의 개수가 최소가 되게 그린거다.
f(x)는 x=α에서 기울기가 0이므로
x-α는 무조건 f(x)와 3번 만나게 되고
x-β는 무조건 f(x)와 x=β에서 한번은 만나야하고
x가 작은 곳에서 f(x)의 감소율이 더 크기때문에
어딘가에서 한번 또 만나야한다.
교점이 최소 5개 생긴다. 따라서 첫번째건 탈락이다.
2.

만나는 점의 개수가 최소가 되게 그린거다.
f(x)는 x=β에서 기울기가 0이므로
x-β는 무조건 f(x)와 3번 만나게 되고
x-α는 무조건 f(x)와 x=α에서 한번은 만나야하고
x가 큰 곳에서 f(x)의 증가율이 더 크기때문에
어딘가에서 한번 또 만나야한다.
교점이 최소 5개 생긴다. 따라서 두번째것도 탈락이다.
3.
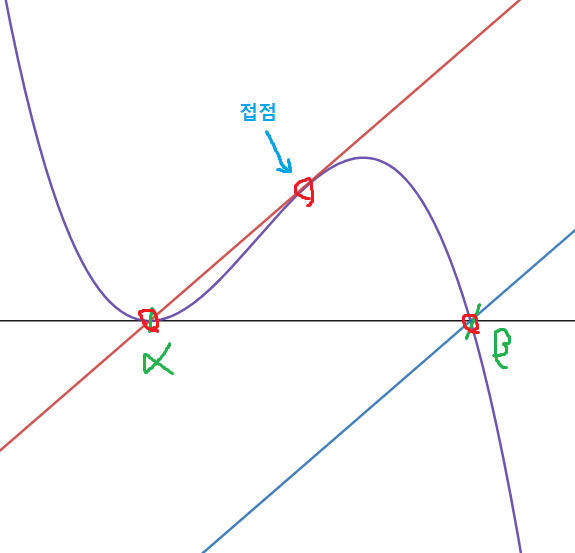
x-α는 무조건 f(x)와 x=α에서 한번 만나게 되고
x-β는 무조건 f(x)와 x=β에서 한번 만나게 된다.
여기서 x-α 와 f(x)가 저 지점에서 접한다면
교점이 3개가 되고 (나) 조건을 만족할 수 있다.
4.

x-β는 무조건 f(x)와 x=β에서 한번 만나게 되고
x-α는 무조건 f(x)와 x=α에서 한번 만나게 된다.
여기서 x-β 와 f(x)가 저 지점에서 접한다면
교점이 3개가 되고 (나) 조건을 만족할 수 있다.
즉 둘 중 하나다.

근데 문제의 조건에서
f(1) = 4 이고 f'(1) = 1 이라고 한다.
근데 왼쪽건 f(1)=4일때 f'(1)<0 이므로
이 조건을 만족하지 못한다.
따라서 저 둘중 왼쪽건 탈락이다.
따라서 f(x) 그래프의 개형을 찾아낼 수 있다.

f(x)는 이렇게 생겼다.
따라서 f(x)의 최고차항을 m 이라 하면
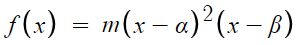

이 그림대로 가게 될것이다.
근데 f'(0)>1 이다.
저런 그래프에서 f'(x)=1 이 되는 지점은 두개밖에 없다.
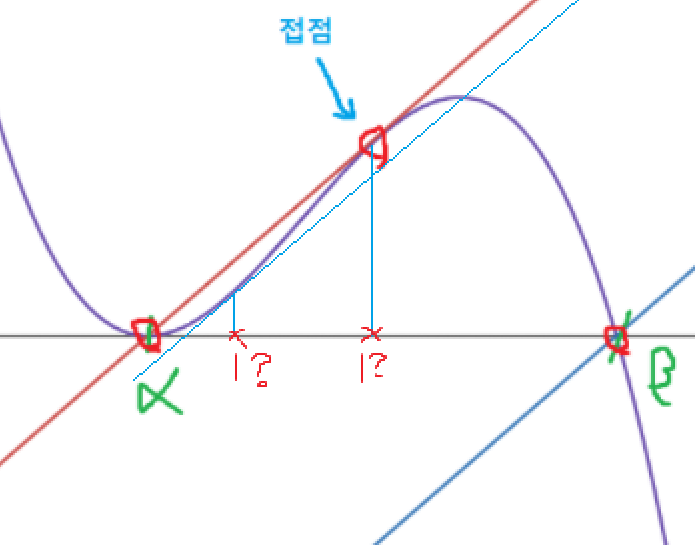
저 둘 중 하나가 1인데
f'(0)>1 이어야 하므로
왼쪽은 1이 될 수 없다.
왼쪽 지점은
기울기가 증가하고 있는 중에서의 지점이기 때문이다.

따라서 x-α 는 x=1에서 f(x)와 접하고
그 지점에서의 y값이 4이다.
따라서 4 = 1-α
따라서 α = -3 이다.
f(x)의 최고차항의 계수를 m이라 하고
문제에 제시된 조건을 만족하는 β와 m을
찾아내면 된다.

따라서 답은 61
'2022학년도 기출 해설 > 2022학년도 6월 모의평가 해설' 카테고리의 다른 글
| 2022학년도 6월 모의평가 수학 확률과통계 23번~30번 해설 (0) | 2021.12.26 |
|---|---|
| 2022학년도 6월 모의평가 물리II 해설 (0) | 2021.09.01 |
| 2022학년도 6월 모의평가 물리I 해설 (0) | 2021.08.31 |
| 2022학년도 6월 모의평가 수학 미적분 23번~30번 해설 (0) | 2021.08.31 |
| 2022학년도 6월 모의평가 수학 공통 1번~15번 해설 (0) | 2021.08.30 |



