선분의 내분점과 외분점

- 개요 -
내용은 어렵지 않은데
공식이 복잡하게 생겨서 '어려워보이는' 곳이다.
- 내분과 외분 -
우선 내분점, 외분점을 다루기 전에
내분, 외분이 뭔지부터 알아야한다.
내분(內分) : 선분을 선분 안쪽에서 두 부분으로 나누는 것
內(안 내), 分(나눌 분) 즉 안에서 나눈다.
외분(外分) : 선분을 선분 바깥쪽에서 두 부분으로 나누는 것
外(바깥 외), 分(나눌 분) 즉 바깥에서 나눈다.
내분점 : 내분하는 점. 내분이기때문에 선분 안에 있다.
외분점 : 외분하는 점. 외분이기때문에 선분 밖에 있다.

내분을 요약하자면 위와 같고

외분을 요약하자면 위와 같다.
- 내분점 -
우리는 내분점을 수식으로 다룰수 있어야한다.
예를 들자면, 선분 AB를 1:2 로 내분하는 내분점은 어디인가? 라고 물으면
찾을수 있어야한다.
우선 내분한다는건 알겠는데 1:2로 내분한다는건 무슨말인가?

아까처럼 선분 AB가 있다고 해보자.
이때 선분 AB를 1:2로 내분한다는건

내분점을 P라 했을 때,
AP의 길이와 PB의 길이의 비가 1:2가 되도록 하라는 말이다.
즉 A와 B 사이를 내분할건데 1:2로 내분 하라는거는
나누는 지점을 정확히 집어주는 표현이라 보면 된다.
AP의 길이와 PB의 길이의 비가 1:2 가 되도록 하는 P점은
선분 AB 위에 하나만 존재할거기 때문이다.

그래서 결론은,
선분 AB를 1:2 로 내분하라는 거는
선분 AB를 1:2로 나누라는건데
여기서 어느쪽을 1로 하고 어느쪽을 2로 할지는
선분 AB를 나누라 했으므로
A에서 B로 가는 방향으로 생각해야한다.
즉 AP 쪽이 1이고 PB 쪽이 2 가 되어야 한다.

예시를 가져왔다.
P는 내분점이다.
그리고 정확히는 선분 AB를 3:2로 내분하는 내분점이다.
따라서 AP : PB = 3 : 2 이다.
- 내분점의 일반화 -

점 P가 선분 AB 위에 있고,

위 식이 성립한다면,
이때 점 P를 선분 AB를 m:n 으로 내분하는 내분점 이라고 한다.
물론 m과 n은 양수여야한다.
m과 n은 길이의 비를 나타내는것이므로
길이는 음수가 될수 없으며, 0도 될수 없다.
- 수직선 위의 선분의 내분점의 좌표 -

여기서 P가 내분점인데,
P의 좌표를 표현할수 있어야한다.
A의 좌표를 a, B의 좌표를 b
P의 좌표를 x라 하겠다.


그다음 위 식을 이용하기 위해
두 점 사이의 거리 공식을 쓴다.

비례식의 성질에 의해
A : B = C : D 면 BC = AD 가 성립한다.
우리가 원하는건 x니까
x에 대한 식으로 나타내려면
좌변엔 x만 남기고
나머지는 전부 우변으로 넘겨야한다.

따라서, 선분 AB를 m:n으로 내분하는
내분점의 좌표는 아래와 같다.

b = B의 좌표, a = A의 좌표
- 내분점공식의 다른 증명법 : 직관적인 설명 -
위의 비례식 증명법이 이해가 안되면
이걸로 이해해도 좋다.

길이가 m:n 이라는건
선분 AB를 (m+n)칸으로 나눴을 때
AP에 m칸, PB에 n칸 배정된다는 뜻이다.

그럼 P의 좌표는?
A에서 m칸만큼 간 곳이다.
A의 좌표는 a이며
한칸의 길이는
선분 AB의 길이를 m+n 칸으로 나눴으니

P의 좌표는 A에서 m칸만큼 간곳이다.
따라서 P점의 좌표는 다음과 같다.
여기서는 b>a 이기 때문에 |b-a| = b-a 이다.
이걸 정리하면 아까 비례식세워서 구했던것과 똑같은 결과가 나온다.

그리고 주의할건, a>b 이면 a가 b보다 크다는거니까
반대로 a에서 m칸만큼 빼준곳이 P의 좌표가 될것이다.
- 심화 : 좌표평면 위의 선분의 내분점 -
심화라고 적어놓긴 했지만 아무것도 없는곳이다.


P의 x좌표는 A의 x좌표와 B의 x좌표를 m:n 으로 내분하는 지점이며
P의 y좌표도 A의 y좌표와 B의 y좌표를 m:n 으로 내분하는 지점이다.
혹시 이게 이해가 안된다면 중등수학이 부족한거다.
중등수학의 '평행선 정리' 를 검색해보자. 증명이 매우 간단해서 그냥 보면 된다.
따라서 그냥 하던대로 하면 된다.
수직선에선 x만 있었지만 여기선 y가 추가된거라 보면 된다.

따라서, 여기서 내분점 P의 x, y의 좌표는 아래와 같다.

즉, 그냥 x 따로 y 따로 하면 된다.
내분점을 두번 구한다고 보면 된다.
- 연습 -
수직선 위의 두 점 A(6), B(-2)에 대하여
선분 AB를 2:3 으로 내분하는 점 P의 좌표를 구하시오.
점 P의 좌표를 x라 하면

따라서 답은 14/5
아까 설명했던 m+n칸 나누기로 설명해도 된다.

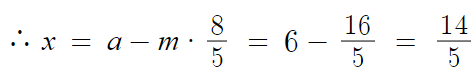
이 문제에선 a>b 이기 때문에
a에서 m칸 빼는 방향으로 가야한다.
따라서 답은 14/5
- 외분점 -
외분점도 수식으로 다룰수 있어야한다.
예를 들자면, 선분 AB를 2:1 로 외분하는 외분점은 어디인가? 라고 물으면
찾을수 있어야한다.
우선 외분한다는건 알겠는데 2:1로 외분한다는건 무슨말인가?

아까처럼 선분 AB가 있다고 해보자.
이때 선분 AB를 2:1로 외분한다는건

외분점을 P라 했을 때,
AP의 길이와 PB의 길이의 비가 2:1이 되도록 하라는 말이다.
즉 A와 B 사이를 외분할건데 2:1로 외분 하라는거는
나누는 지점을 정확히 집어주는 표현이라 보면 된다.
AP의 길이와 PB의 길이의 비가 2:1 가 되도록 하는 P점은
선분 AB 밖에 하나만 존재할거기 때문이다.

그래서 결론은,
선분 AB를 2:1 로 외분하라는 거는
AP와 BP를 2:1로 나누라는건데
여기서 어느쪽을 2로 하고 어느쪽을 1로 할지는
선분 AB를 나누라 했으므로
A에서 B로 가는 방향으로 생각해야한다.
즉 AP 쪽이 2이고 BP 쪽이 1이 되어야 한다.

예시를 가져왔다.
P는 외분점이다.
그리고 정확히는 선분 AB를 2:3으로 외분하는 외분점이다.
따라서 AP : BP = 2 : 3 이다.
- 외분점의 일반화 -

점 P가 선분 AB의 연장선에 있고,

위 식이 성립한다면,
이때 점 P를 선분 AB를 m:n 으로 외분하는 외분점 이라고 한다.
물론 m과 n은 양수여야한다.
m과 n은 길이의 비를 나타내는것이므로
길이는 음수가 될수 없으며, 0도 될수 없다.
그리고, m=n도 될수 없다. 그 이유는
상식적으로 생각해보자. 1:1 외분점을 찾아보자. 그런건 없다.
- 수직선 위의 선분의 외분점의 좌표 -

여기서 P가 외분점인데,
P의 좌표를 표현할수 있어야한다.
A의 좌표를 a, B의 좌표를 b
P의 좌표를 x라 하겠다.


그다음 위 식을 이용하기 위해
두 점 사이의 거리 공식을 쓴다.

따라서, 선분 AB를 m:n으로 외분하는
외분점의 좌표는 아래와 같다.

b = B의 좌표, a = A의 좌표
추가로, m=n이면 안되는 이유가 여기서도 나온다.
m=n이면 0으로 나누는 말도안되는 연산을 해야한다.
수식적으로도 말이 안되고 상식적으로도 말이 안되는것이다.
- 외분점공식의 다른 증명법 : 직관적인 설명 -
위의 비례식 증명법이 이해가 안되면
이걸로 이해해도 좋다.

길이가 m:n 이라는건
선분 AB를 m-n칸으로 나눴을 때
AP에 m칸, PB에 n칸 배정된다는 뜻이다.

그럼 P의 좌표는?
A에서 m칸만큼 간 곳이다.
A의 좌표는 a이며
한칸의 길이는
선분 AB의 길이를 m-n 칸으로 나눴으니

P의 좌표는 A에서 m칸만큼 간곳이다.
따라서 P점의 좌표는 다음과 같다.
여기서는 b>a 이기 때문에 |b-a| = b-a 이다.
이걸 정리하면 아까 비례식세워서 구했던것과 똑같은 결과가 나온다.

그리고 주의할건, a>b 이면 a가 b보다 크다는거니까
반대로 a에서 m칸만큼 빼준곳이 P의 좌표가 될것이다.
추가로, n>m 이면 분모가 음수가 나오게 되는데
n>m 이면 P점은 A와 B중 A에 가깝게 위치하게 된다.
따라서 점 A에서 반대방향으로가야하고 그래서 음수가 나온것이다.
- 심화 : 좌표평면 위의 선분의 외분점 -
내분점과 완전히 논리가 똑같기때문에
자세한 설명은 생략한다.

- 예제 -
1 )

좌표평면 위의 선분의 내분점 문제이다.
그냥 x 따로 y 따로 하면 된다고 했었다.
점 P의 좌표를 P(x, y)라 하겠다.
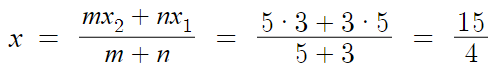

따라서 답은 (15/4, -3)
아까 설명했던 직관적 m+n칸 나누기로 풀어도 된다.
우선 B의 x좌표가 A의 x좌표보다 작으므로
A에서 B를 향해 가기위해 A에서 m칸만큼 빼주면 된다.
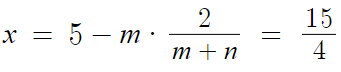
y도 같은논리로 하면 된다. 생략
2 )

좌표평면 위의 선분의 외분점 문제이다.
점 Q의 좌표를 Q(x, y) 라 하면


따라서 답은 (1, -14)
아까 설명했던 직관적 m-n칸 나누기로 풀어도 된다.
B의 x좌표가 A의 x좌표보다 작고
m>n 이므로
점 Q는 A와 B중 B에 가깝게 위치한다.
따라서 A에서 Q점까지 가기 위해서는 m칸 빼주면 된다.
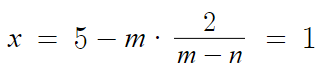
y도 같은 논리로 하면 되니 생략
3 )

중점 : 가운데지점
즉 A와 B 사이의 딱 중간지점
즉 선분 AB를 1:1로 내분하는 내분점
따라서 M은 선분 AB를 1:1로 내분하는 내분점이다.


따라서 답은 (4, -2)
중간지점이라는건 둘의 평균이라는거니까
x좌표는 (5+3)/2 = 4
y좌표는 (2-6)/2 = -2
따라서 답은 (4, -2)
이렇게 간단히 답을 낼수도 있다.

