삼각형의 무게중심

- 개요 -
우리는 지금까지
삼각형의 오심(五心) 중 세가지를 배웠다.
외심, 내심, 무게중심이다.
이번엔 그 무게중심을 복습하는시간이다.
무게중심을 설명하려면 선분의 내분을 알아야하기때문에 여기에 배치된것이다.
- 무게중심의 정의 -

특별한거 없이 아무렇게나 생긴 삼각형이 있다고 해보자.
삼각형의 무게중심 : 삼각형의 세 중선의 교점
중선 : 꼭짓점과 마주보고있는 선분의 중점을 연결한 선
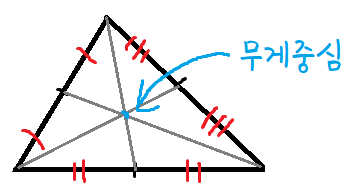
그리고 무게중심은 보통 G라고 쓴다.
무게중심 이니까 중력과 연관이 깊은 점이다.
중력은 영어로 gravity이고 앞글자 따온거다.
- 무게중심의 성질 -
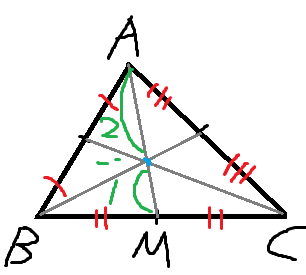
무게중심은 중선을 2:1로 내분하는 내분점이다.
왜 2:1로 내분하는가?
차근차근 설명해주겠다.

우선 M은 선분 BC의 중점이므로
삼각형 BGM과 삼각형 CGM의 넓이가 같다.
밑변길이도 같고 높이도 같기때문이다.

선분 AB의 중점을 L이라 하고,
선분 AC의 중점을 N이라 하면
아까와 같은 논리로
삼각형 AGL과 BGL의 넓이가 같고
삼각형 AGN과 CGN의 넓이도 같다.
그리고 삼각형 ABM과 ACM도 넓이가 같다.
밑변길이 같고 높이 같기때문이다.
따라서 b=c 이다.
나머지에도 똑같은 논리를 적용해보면
삼각형 ABN과 BCN의 넓이 같을거고
그러면 a=c 이다.
따라서 a=b=c 이고
저렇게 나뉜 6개의 삼각형의 넓이가 모두 같다는 결론에 도달한다.
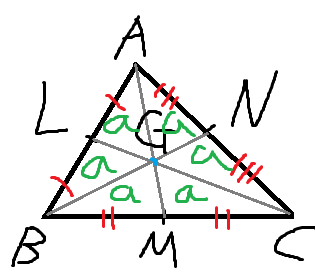
이것도 무게중심의 성질중 하나니 알아두자.
이제 왜 G가 2:1 내분점인지를 설명할때다.

삼각형 GBC의 넓이는 2a 이다.
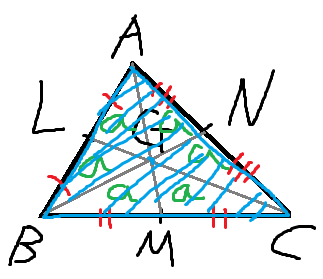
삼각형 ABC의 넓이는 6a이다.
삼각형 GBC와 ABC는 밑변이 BC로 같으니
삼각형 ABC의 높이가 삼각형 GBC의 높이의 3배라는 결론을 얻을 수 있다.
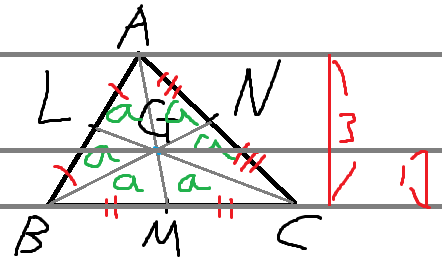
따라서 평행선의 성질에 의해
AG의 길이 : GM의 길이 = 2 : 1 이다.
따라서 G는 선분 AM를 2:1로 내분하는 내분점이다.
- 무게중심의 좌표 -
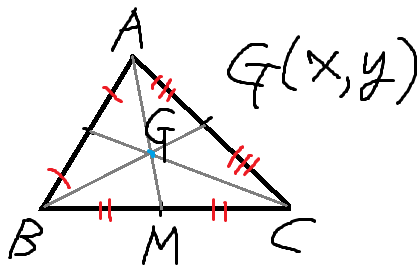
G의 좌표를 구해볼것이다.
A의 좌표를 A(x₁, y₁)
B의 좌표를 B(x₂, y₂)
C의 좌표를 C(x₃, y₃)
이라 하겠다.
그러면 M은 선분 BC의 중점이므로
M의 좌표는 아래와 같다.
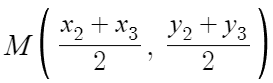
아까도 설명했듯이 무게중심의 성질에 따라서
점 G는 선분 AM을 2:1로 내분하는 내분점이다.
따라서 G의 좌표를 내분점 공식을 이용해 구하면
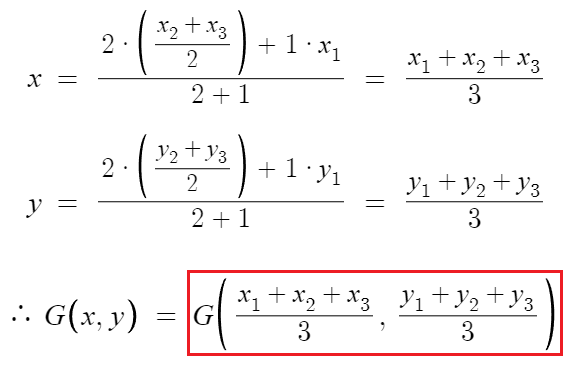
결론은, 삼각형의 무게중심의 좌표는
세 꼭짓점의 좌표의 평균값이다.
- 예제 -

무게중심의 좌표는 세 꼭짓점의 좌표의 평균값이다.
따라서, 아래 식이 성립한다.
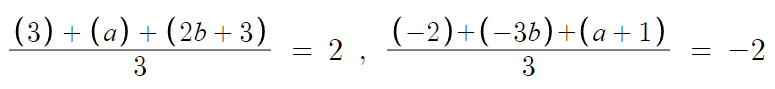
이걸 정리하면 a와 b에 대한 관계식이 두개가 나올테니
a와 b의 값을 구하기 위해서는 둘을 연립하면 될것이다.
둘다 정리하면
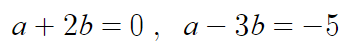
이 둘을 뺄셈연립하면
5b = 5 따라서 b=1
따라서 a=-2
따라서 ab=-2 이고 답은 -2