자취의 방정식 - 점의 자취

- 개요 -
자취의 방정식을 구하라는 문제가 나오기도 하는데
문제가 뭔말인지 이해를 못해서 어려워하는 학생이 많아서 따로 글을 적는다.
- 자취 -
우선 자취가 뭔지부터 알 필요가 있다.
대학생들이 하는 자취랑은 관련없는단어이다.
자취 : 일정한 조건을 만족하면서 움직이는 점이나 선이 그리는 도형.
쉽게 말해서, 특정한 조건을 만족하는 점들이 있을텐데
그 점을 모두 모아서 그려지는 도형이 바로 자취이다.
발자취와 비슷한 느낌으로 이해하면 된다.
예를 들어, xy 좌표평면에서 자취를 구하라고 하면
x와 y가 어떠한 특정 조건을 만족하는 점이 있을거고
그걸 (x,y)로 좌표평면에 표현할수 있을거 아닌가?
그렇게 표현되는 점을 모두 모아서 도형으로 그리라는 말이다.
그리고 이렇게 구한 자취를 x와 y 사이의 관계식, 즉 방정식으로 나타내면
그게 바로 자취의 방정식이다.
즉, 자취의 방정식이라는건 도형의 방정식 구하라는거다.
요약하자면,
자취의 방정식 : 특정 조건을 만족하는 x와 y 사이의 관계식
- 문제 풀어보기 -

처음이니까 같이 풀어주겠다.
점 Q의 자취부터 구할거다.
점 Q의 좌표를 Q(x, y)라 하겠다.
점 P의 좌표는 P(a, b)라 하겠다.
그러면 점 A(2, 4)와 점 P(a, b)를 이은 선분 AP를
1:2 로 내분하는 점 Q의 좌표를 구할 수 있다.

이제 a와 b 사이의 관계만 정리하면 되는데
이 문제에서 첫문장이 좀 중요하다.
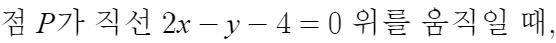
점 P가 직선 2x-y-4=0 위를 움직인다는건
점 P는 직선 2x-y-4=0 을 만족하는곳에서만 존재한다는 뜻이고
이는 점 P의 자취의 방정식이 2x-y-4=0 임을 의미한다.
따라서 P(a, b)에서 a와 b를 대입하면

이제 아까 구한 Q점의 x, y 좌표에다가
이걸 대입하자.

x는 a에 대한 식이고 y는 b에 대한 식인데
우리는 x와 y의 관계식을 구할거니까
x를 b에 대해서 나타내주면 x와 y의 관계를 알수 있을것이다.
a = b/2 + 2 를 대입하면

이제 x와 y가 둘다 b에 대한 식이니까
x와 y의 관계를 구할수 있다.

양변에 8만 더해주면 끝
따라서 답은 6x-4 = 3y
- 예제 -

구하고자 하는 점을 P라고 하고
점 P의 좌표를 P(x, y)라 하겠다.
점 P의 자취의 방정식을 구하면 된다.
점 A와 P 사이의 거리 = 점 B와 P 사이의 거리
따라서 점과 점 사이의 거리 공식을 이용해 관계식을 세우면
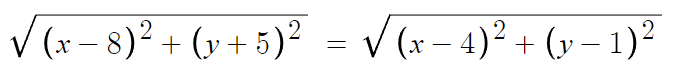
루트 있으면 계산이 곤란하니 양변을 제곱하면
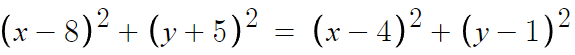
좌변과 우변을 전개해서 다시쓰면
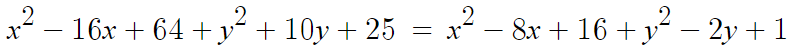
이제 식을 정리만 하면 된다. 정리하면
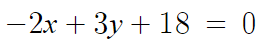
따라서 답은 -2x+3y+18 = 0