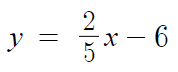직선의 방정식 #3 - 두 직선의 평행과 수직

- 개요 : 두 직선의 위치관계 -
이번에 다룰건
'두 직선'의 '위치관계' 이다.
두 직선이 서로 평행한가? 수직인가? 둘다 아닌가? 이런걸 다룰것이다.
- 두 직선의 평행 -

이러한 두 직선이 있다고 해보자.
두 직선이 평행할 조건은?
평행하다 : 기울기가 같다.
따라서 평행하려면 m=m' 이어야한다.
그럼 m=m' 이면 기울기가 같으니까 무조건 평행하느냐?
그건 아닌게, 두 직선이 완전히 똑같은 직선이면
그건 그냥 두 직선이 완전히 똑같은거라 둘이 '일치한다'고 표현하지
평행한다고 표현하지는 않는다.
즉 평행하려면 m=m' 이어야하지만 n=n' 이면 안된다.
따라서 정리하자면,

근데 직선의 방정식이 저런 표준형만 있지는 않다. 일반형도 있다.

근데 일반형도 똑같다.
'평행하다 : 기울기가 같다' 라는게 핵심 논리이기 때문이다.
저 식에서 기울기는 무엇인가?
ax 이항하고 b 나누면 -a/b 임을 알수 있다.
따라서 위쪽 식에서 기울기는 -a/b 이고
아래쪽 식에서 기울기는 -a'/b' 이다.
따라서 평행하려면 -a/b = -a'/b' 이어야한다.
여기까지 정리하면

근데, 여기서도 완전히 같은식이 되지 못하게 c≠c' 이어야 하는가?
그건 아니다.
일반형에서는 c=c' 여도 평행할수 있다.
예시를 들어주겠다.
2x+y+1 = 0
4x+2y+1 = 0
둘의 기울기도 같고 상수항의 값도 1로 같다.
하지만 두 식은 표준형으로 바꿔보면 알겠지만 다른 식이다.
어떻게 이런일이 있을수 있냐면
표준형은 무조건 y=~~ 형태라서
x의 계수가 무조건 기울기이며
상수항의 값이 무조건 y절편이다.
그래서 기울기와 상수항의 값이 둘다 같으면 안되는거다.
하지만 일반형에서는
기울기와 y절편이 식에 바로 써있는게 아니다.
기울기를 구하려면 a와 b의 비율을 구하는 나눗셈연산을 해야하고
y절편을 구하려면 b와 c의 비율을 구하는 나눗셈연산을 해야한다.
즉 일반형에서 기울기와 y절편은 두 계수의 비율로 되어있다.
그래서 꼭 c≠c' 이어야할 필요는 없다.
c=c' 이어도 a와 b의 값에따라 y절편이 달라지기 때문이다.
굳이 따지자면, -c/b ≠ -c'/b' 이어야한다.
여기까지 정리하면, 아래와 같다.

- 연습 -
두 직선 y = -2x+a , y = (2m+1)x+4 가
서로 평행하기 위한 m의 값을 구하고, a의 조건을 설명하시오.
두 직선이 평행하다 = 기울기가 같다.
따라서 -2 = 2m+1 이고
정리하면 m=-3/2 이다.
그리고 기울기가 같아도 y절편(상수항의 값)이 같으면 평행하다고 할수 없다.
따라서 a≠4 여야한다.
따라서 답은 m=-3/2 , a≠4
- 두 직선의 수직 -

핵심 : 기울기의 곱이 -1이면 수직이다.
이건 무조건이다. 기울기의 곱이 -1이라는건
일단 기울기가 다르다는거니까 두 직선은 절대로 같지 않다.
따라서 이때는 n과 n'의 값은 생각하지 않아도 된다.
기울기의 곱이 -1이면 무조건 수직이다.
근데 왜 -1이면 수직인가?
중등수학으로 증명 가능하다.

직각삼각형이 있다고 해보자.

빗변은 x축과 평행하며,
그림처럼 수선을 내린다.
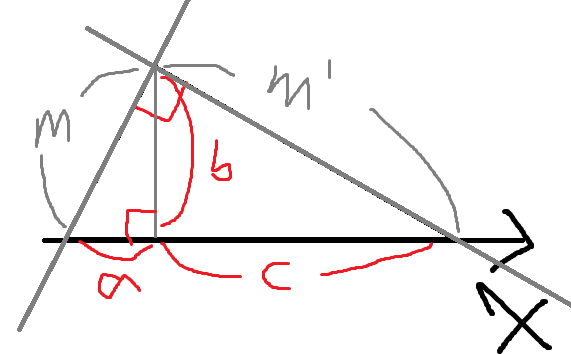
빗변을 제외한 두 선분에서 연장선을 그린다음
각각 기울기 m, m'인 직선이라고 해보자.
그러면 왼쪽 직선의 기울기는 b/a 이며
오른쪽 직선의 기울기는 -b/c 이다.
두 직선의 기울기를 곱하면

근데 중2때 배우는 삼각형의 닮음에 의해
b² = ac 이다.
이걸 대입만 해주면 증명이 간단하게 완료된다.

따라서, 아래와 같은 결론을 얻는다.

여기서 m과 m'은 두 직선의 기울기이다.
이 논리는 당연히 일반형에도 적용된다.

- 예제 -
1 )

서로 수직이다 = 기울기의 곱이 -1이다.
왼쪽 방정식에서 기울기는 -a/3 이며
오른쪽 방정식에서 기울기는 1/(a+4) 이다.
둘을 곱해서 -1이면 된다.
따라서, 다음과 같은 관계식을 세울 수 있다.
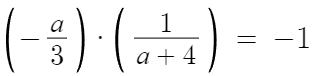
양변에 -3(a+4) 곱하면 a=3a+12 이고 따라서 a=-6
따라서 답은 -6
2 )

평행하다 = 기울기가 같다. 단 완전히 똑같은직선이면 안된다.
직선 2x-5y+3=0 의 기울기는 2/5 이다.
따라서 우리가 구하고자 하는 직선의 기울기도 2/5 이다.
그럼 기울기를 아니까 직선의 방정식을 표준형으로
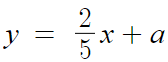
여기까지 작성할 수 있다.
얘가 점 (10, -2) 를 지난다 하니
각각 대입해주면 a의 값이 나올거고 그걸로 마무리하면 되겠다.
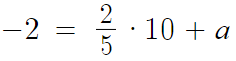
따라서 a=-6 이다.
따라서, 다음과 같은 직선의 방정식을 얻는다.
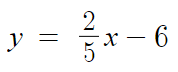
근데 아직 끝내면 안되는게,
두 직선이 기울기가 같은거지
아직 완전히 같은직선 즉 일치하는 직선인지는 확인하지 않았다.
물론 이 문제에서는 일치해버리면 문제 자체가 오류기 때문에 일치할리가 없겠지만,
다른문제에서는 확인해야할수도 있으니
잊어버리지말고 꼭 확인하자. 쉬운데서 실수해서 틀리면 화난다.
2x-5y+3=0
y=(2/5)x-6
이 두개가 같은식이면 일치하는거라서 안된다.
표준형쪽을 일반형쪽으로 바꾸던지
일반형쪽을 표준형쪽으로 바꾸던지
둘다 (0, 0)을 대입해보던지
방법은 맘대로 해도 된다. 아무튼 확인해보면 일치하지 않음을 알수 있다.
따라서 y=(2/5)x-6 은 평행한 직선이 맞다.
따라서 답은