원의 방정식 #2 - 두 원의 교점을 지나는 원과 직선의 방정식

- 개요 -
제목 그대로
두 원의 교점을 지나는 원의 방정식
두 원의 교점을 지나는 직선의 방정식
을 구해볼것이다.
- 두 원의 교점을 지나는 원의 방정식 -
두 직선의 교점을 지나는 직선의 방정식을 구할때와 논리가 똑같다.
교점 = 연립방정식의 해
따라서, 두 원의 교점을 지나는 원의 방정식은
아래와 같이 쓸 수 있다.

왼쪽부분과 오른쪽부분이 둘다 0이면 k에 상관없이 항상 성립하니까
저렇게 원의 방정식을 작성하면,
연립방정식의 해인 두 원의 교점을 지날수밖에 없다.
이해가 안되면, 두 직선의 교점을 지나는 직선의 방정식을 다시 공부하고 오자.
Q) 원의 방정식은 이차항의 계수가 1이어야 하지 않나요?
A) 좋은 질문이다. 저 식을 전개해보면 답을 알 수 있다.
편의상 이차항만 전개하겠다.

이제 양변을 1+k로 나눠주면?
이차항의 계수가 1만 남게된다.
따라서 저것도 원의 방정식이 맞다.
Q) k=-1 이면 1+k로 못나누는데요?
A) k=-1이면 1+k=0 이라서 이차항 자체가 사라진다.
따라서 이건 원이 아니라 직선의 방정식이 된다.
- 문제 풀어보기 -

처음이니까 같이 풀어주겠다.
우선 두 원의 교점을 지나는 원의 방정식은
아까처럼 작성하면 된다.

k값만 구해주면 끝날텐데 k값은 어떻게 구하느냐?
그래서 이 원이 지나는 점의 좌표를 알려준다.
점 (1, 3)을 지난다고 하니
x=1, y=3을 대입해서 정리하면 k값이 나올것이다.

정리하면 3+2k=0 따라서 k=-3/2 이다.
이제 k값을 대입해서 정리하면 끝이다.


저대로 끝내도 되지만
우리는 여태 이차항의 계수가 1인것만 다뤄왔으니
이것도 이차항의 계수를 1로 맞춰주자.
양변에 -2를 곱하면 될것이다.
곱해주면 답은

- 두 원의 교점을 지나는 직선의 방정식 -

두 원의 공통인 현의 방정식 이라고도 한다.
이게 두 원의 교점을 지나는 원의 방정식이라 했는데
아까 k=-1 이면 이차항의 계수가 0이되면서
직선의 방정식이 된다고 했었다.
그게 핵심 idea이다.
k=-1 이라 두는것이다.
원의 방정식은 바로 작성할수 있고
그 원의 방정식에서 이차항만 소거시키면 일차항만 남고
그러면 직선의 방정식이 될것이라는 논리이다.
저 식을 만족하는 x,y 해가 두 원의 교점이라는건 자명한 사실이고
그 점을 지나는 방정식은 k의 값에따라 달라지도록 아주 많이 존재하는데
여기서 k=-1이라 둬버리면 직선의 방정식이 되어버리는 것이다.
k=-1이면 x와 y에 대한 일차식, 즉 직선의 방정식이 되기 때문이다.
위 식에 k=-1을 대입하고 정리하면

결론을 외우지 말고 idea가 무엇이었는지를 이해하는게 중요하다.
어느정도 해야 이해한건지 모르겠다면 가이드라인을 제시해주겠다.
이 내용을 다른사람에게 가르칠 수 있는 수준이면 된거다.
- 예제 -
1 )

두 원의 교점을 지나는 원의 방정식을 작성하면
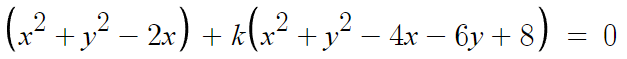
교점을 지나긴 하는데 k값을 몰라서 정확히 어떤 원인지 모르겠다.
따라서 이 원이 지난다는 점 (0, 1)을 대입한다.
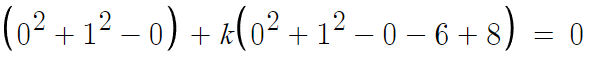
따라서 k=-1/3 이다.
이제 원의 방정식을 완성시킬 수 있다.

분수가 꼴보기싫으니 양변에 3을 곱해버리자.

원의 방정식을 찾아냈다.
이제 넓이를 구하면 되는데
원의 넓이 = πr² 이므로, 넓이를 구하려면 반지름(r)을 알아야한다.
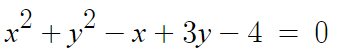
근데 이 식은 일반형이라서 반지름이 바로 눈에 보이지 않는다.
따라서 식을 표준형으로 바꾼다.
표준형은 식 자체에 반지름이 있기 때문에, 표준형으로 바꾸면 반지름을 찾기 쉽다.

따라서 r² = 13/2 이고
따라서 답은 13π/2 이다.
2 )

두 원의 교점을 지나는 원의 방정식을 작성한 뒤
이차항을 소거시키면 된다.

이게 두 원의 교점을 지나는 원의 방정식인데,
여기서 k=-1 이라 두면 이차항이 소거된다.

이걸 정리하면, 답은
6x-10y-13 = 0