원의 방정식 #3 - 원과 직선의 위치관계

- 개요 -
직선의 방정식 에서는
직선과 직선의 위치관계를 다뤘었다.
이번엔 원과 직선의 위치관계를 다룰것이다.
- 원과 직선의 위치관계 -
원과 직선의 위치관계를 논할때
가장 중요한것은, '원과 직선이 만나느냐, 만나지 않느냐' 이다.
만나거나, 만나지 않거나 둘중 하나이며,
만나는 경우도, 두 점에서 만나거나 한 점에서 만나거나 둘중 하나이다.
이걸 그림으로 요약하자면 아래와 같다.

그럼 만나는지 안만나는지는 어떻게 판별하는가?
'원의 중심과 직선 사이의 거리' 와
'원의 반지름' 을
비교하면 된다.
왜냐?
원의 중심과 직선 사이의 거리가 원의 반지름보다 커버리면
원과 직선은 절대로 만날 수 없기 때문이다.
쉽게 말해서, 너무 멀다.
여기서 원의 중심과 직선 사이의 거리를 d(distance)
원의 반지름을 r(radius)이라 하면
d>r 이면 만나지 않는것이다.
따라서, 다음과 같은 결론을 얻는다.

근데 아직 끝나지 않았다.
한번 만날수도 있고 두번 만날수도 있다.
이것도 d와 r을 비교하면 된다.
만약 d=r 이면?
원의 중심과 직선 사이의 거리가 원의 반지름과 같다는거다.
이럴때 이 직선은 이 원의 '접선'이 되는것이다.
원의 접선은 원과 한 점에서 만나고, 이걸 접한다고 한다.
따라서 d=r이면 원과 한 번 만난다.
따라서, 최종적으로 다음과 같은 결론을 얻는다.

그리고, 판별식을 이용해서 판별하는 방법도 있는데
쓸데없이 어렵기만하고 전혀 필요없는거라서 나는 다루지 않겠다.
- 예제 -

원과 직선의 위치 관계를 논할 때는
원의 중심과 직선 사이의 거리와 반지름을 비교한다.
서로 다른 두 점에서 만난다고 하니, d<r 이면 된다.
원의 중심은 (0, 0)이며,
직선의 방정식은 x-y+k=0 이다.
d의 값을 구하기 위해, 점과 직선 사이의 거리 공식을 적용하면

그리고 원의 방정식을 보면 표준형이다.
따라서 9는 반지름의 제곱이고, 따라서 반지름은 3이다.
따라서 r=3 이다.
이제 두 점에서 만나기 위한 조건인 d<r에다
구한 d, r 값을 각각 대입해주면 된다.
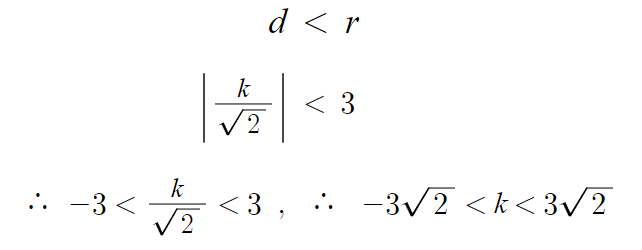
따라서 답은
-3√(2) < k < 3√(2)