점과 도형의 평행이동

- 개요 -
이제 두개만 배우면 수학(상)이 끝난다.
평행이동과 대칭이동이다.
이번엔 평행이동을 다룰것이다.
- 평행이동이란? -
말 그대로 평행하게 이동하는거다.
그냥 평행하게 이동시키는거라
위치만 바뀌지, 모양은 절대 바뀌지 않는다.
- 평행이동 1 : 점의 평행이동 -
점부터 평행이동시켜보자.
이건 아주 쉽다.
예를 들어서,
점 (2, 1)을
x방향으로 +3만큼
y방향으로 -2만큼
평행이동 한다면,
x방향으로 +3 갔으니 x좌표는 5가 되고
y방향으로 -2만큼 갔으니 y좌표는 -1이 되는것이다.
따라서 평행이동된 점의 좌표는 (5, -1)이다.
너무 쉬워서 바로 일반화할수 있다.
점 (x, y)를
x축의 방향으로 a만큼
y축의 방향으로 b만큼 평행이동시키면
그 평행이동된 점의 좌표는
(x', y') 이라고 하면,
x' = x+a
y' = y+b
따라서 평행이동된 점의 좌표는
(x+a, y+b) 이다.
바로 문제를 풀어보자.
점 (-3, -6)을 x축의 방향으로 5만큼, y축의 방향으로 -8만큼 평행이동한 점의 좌표는?
x' = -3+5 = 2
y' = -6-8 = -14
따라서 답은 (2, -14)
- 평행이동 2 : 도형의 평행이동 -
점의 평행이동은 쉬운데,
도형의 평행이동은 쉽지는 않다.
직관적으로 이해가 잘 안돼서 그런건데,
일단 보면 왜 그런 말을 했는지 알게된다.
직선 x-5y+1 = 0을
x축의 방향으로 3만큼
y축의 방향으로 -1만큼 평행이동한
도형의 방정식을 구해보자.
우선 구하는 방법은, 점의 평행이동을 이용하면 된다.
도형에 있는 모든 점이 똑같이 평행이동될거기 때문이다.
도형이라는건 점이 모인거니까
x에 3 더하면 x+3
y에 1 빼주면 y-1
이걸 대입해서
(x+3) -5(y-1) + 1 = 0 이라고 쓰면 될까?
그렇지 않다.
왜 그런지 바로 알아보겠다.
(x+3) -5(y-1) + 1 = 0 은 다른 말로 쓰면
x'-5y'+1 = 0 이라는거다.
근데 내가 x'과 y'의 관계를 알려준적이 있나?
그런적 없다. 그래서 저렇게 쓰면 안된다.
대신 x와 y의 관계는 알고있다. 문제에서 x-5y+1=0 이라고 줬다.
문제에서 준 x와 y사이의 관계를 이용해서 식을 다시써야한다.
x' = x+3 이므로, x = x'-3 이다.
y' = y-1 이므로, y = y'+1 이다.
따라서 저걸 x-5y+1=0 에 대입해야한다.
대입하면, (x'-3) - 5(y'+1) + 1 = 0 이다.
x', y'은 우리가 임시로 잠깐 도입한 문자인데
얘네도 뜻은 x좌표, y좌표라는 뜻이니까
그냥 ' 기호 떼고 (x-3) - 5(y+1) + 1 = 0 이라고 쓰면
이게 답이다.
부호가 반대로 들어간다.
아래에 자세히 설명해주겠다.
근데 여기서 이해가 안 될만한 부분이
저게 x'과 y' 사이의 관계식인데
그냥 처음에 준 식에 대입해서
x'-5y'+1=0 이라고 써도 x'과 y' 사이의 관계식인데
대체 뭐가 다른건가?
우선 내가 방금 작성한 부호 반대로넣은
(x'-3) - 5(y'+1) + 1 = 0 은
x'과 y'의 관계식이 맞다.
근데 x'과 y'은 평행이동된 점이며,
우리는 평행이동된 도형의 방정식을 작성해야한다.
즉 x'과 y'의 관계를 찾아내야한다.
x-5y+1=0 은 x와 y에 대한 관계식이지,
x'과 y'에 대한 관계식이 아니다.
우리가 할건,
x와 y의 관계식을 이용해서
x'과 y'의 관계식을 찾아내는것이다.
근데 답이 x'-5y'+1=0 이라고 하는거는
x-5y+1=0에 그냥 x', y' 대입해서
x'-5y'+1=0 을 써놓고 답이라고 우기고있는것이다.
x'과 y'의 관계식을 구하랬더니
이미 구해져있는 x와 y의 관계식에다가 그냥 넣어버리고는
이게 답이에요 하고있는것이다.
이렇게 보니까 말도안되는 황당한 풀이법 아닌가?
추가로, 평행이동 전의 도형인 x-5y+1=0 과
평행이동 후의 도형인 (x-3) - 5(y+1) + 1 = 0 를
각각 그려보면,
실제로 평행이동은 그래프의 모양에 아무런 영향을 주지 않는다는걸 볼 수 있다.
요약하자면,
도형의 평행이동에서는 부호가 반대로 들어간다.
반대로 들어가는 이유는
x'과 y'의 관계식을 찾는 과정에서
x = x'-3 이런식으로 3이 이항되기 때문에
점은 +3만큼 평행이동되지만
이를 관계식으로 나타내면 -3이 등장하는 것이다.
바로 연습해보자.

첫 문장부터 해석하자면,
점 (x, y)를 x방향으로 -1, y방향으로 +3 만큼
평행이동 했다는거다.
그러면 x' = x-1 , y = y+3 이며
평행이동된 도형의 방정식을 구하려면
평행이동된 점의 좌표인 x'과 y'의 관계식을 구해야한다.
따라서 x = x'+1 , y = y'-3 이라고 다시 쓰고
문제에서 준 방정식인 5x-2y+1=0 에다가 대입해주면 된다.

근데 x'과 y'은 우리가 임시로 잡은 미지수이며
x'과 y'이 각각 x좌표, y좌표라는 뜻이므로
그냥 ' 떼고 다시 적으면 된다.

이걸 정리하면, 답은

- 도형의 평행이동의 일반화 -

혹시 f(x, y)=0 이 무슨 뜻인지 모르나?
f(x) 라는건 x에 대한 함수라는 뜻이고
f(x, y) 라는건 x와 y에 대한 함수라는 뜻이다.
직선의 방정식의 일반형이 그 예이다.
x+3y-2 = 0
여기서 x+3y-2가 x와 y에 대한 함수니까
f(x, y)라고 쓰는것이다.
여담으로, 이런 함수를
변수가 여러개니까 '다변수함수' 라고 한다.
- 예제 -

기본개념에서 한번 꼬아서 나온 문제이다.
평행이동된 도형을 구하는게 아니라,
평행이동 된것에서 원래의 도형을 구하는 문제이다.
혹시 이거 한번 꼬아서 낸 문제라고 못푼다면
그냥 개념 이해못한거니까 다시읽자.
쎈 교재 A단계에 있는 문제이다.
아무튼 문제를 풀어보자면
도형 f(x, y)=0이 도형 f(x+3, y-5)=0 으로 옮겨졌다고 한다.
따라서 이건 x방향으로 -3, y방향으로 5만큼 평행이동 시킨것이다.

얘가 그 결과물인것이다.
따라서 원래의 도형도 원의 방정식일것이다.
원래의 도형의 방정식에다가
그냥 x자리에 x+3, y자리에 y-5 넣은 결과물이기 때문이다.
따라서 평행이동 전의 도형의 방정식을 구할거면
반대로 x방향으로 3, y방향으로 -5만큼 평행이동 시키면 된다.
그러려면
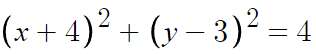
여기다 x-3, y+5 대입해주면 끝난다.
따라서 답은
