
홀수형 기준입니다.
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 24번으로 가고싶으면 24 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
23 )

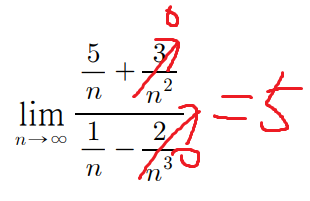
분모 분자에 n을 곱한 뒤 정리하면 답은 5번
24 )

양변을 미분한다음
x³+x = 2 가 되도록 하는 x값이 1이니까
x=1을 대입하면 된다.
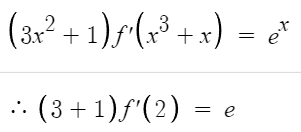
따라서 f'(2) = e/4
답은 4번
25 )

왼쪽것부터 풀어 써보면
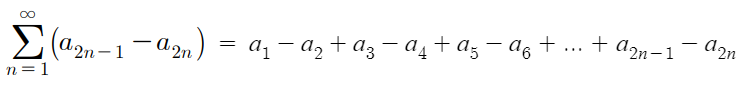
a_n은 등비수열 이므로
a_n의 첫째항을 a, 공비를 r이라 하면
저것의 값은
첫째항이 a이고 공비가 -r 인 등비수열의 합과 같다.
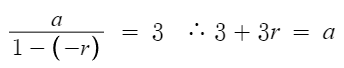
이번엔 오른쪽것을 풀어쓰면

a_n은 등비수열 이므로
저것의 값은
첫째항이 a²이고 공비가 r²인 등비수열의 합과 같다.
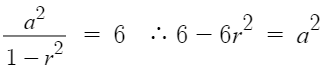
아까 왼쪽 식을 풀면서
a = 3r+3 임을 알았으므로 이를 대입하면
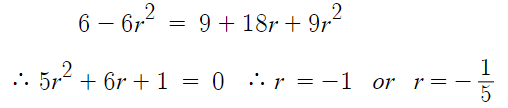
근데 r=-1 이면 왼쪽 식과 오른쪽 식 모두
수열의 극한값이 0이 아니므로 무조건 발산한다.
따라서 r=-1/5 이다.
그리고 a=3r+3 이므로 a = 12/5 이고

따라서 답은 2번
26 )
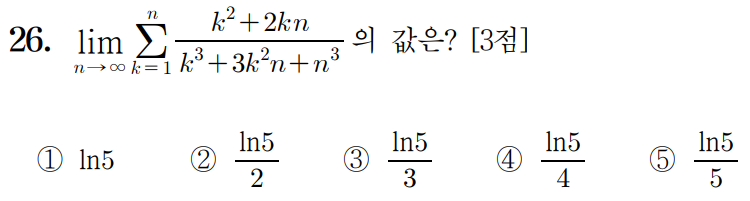
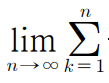
얘가 등장했고
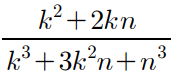
이렇게 k와 n이 등장했으니
이건 정적분과 급수의 관계 문제구나 라고 추론할 수 있다.
근데 정적분과 급수의 관계 문제면
우선 적분할 변수 x, 함수 f(x), dx를 빼내야 하고
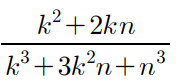
그러기 위해서는 이 식을 변형할 필요가 있어보인다.
분모 분자를 n³ 으로 나눈다.

여기서 k/n = x라 두면
dx = x의 변화량이니까
dx = 1/n 이 된다.
그리고 x = k/n 이니까
적분구간은 x=0 ~ x=1 이다.

이제 적분만 하면 된다.
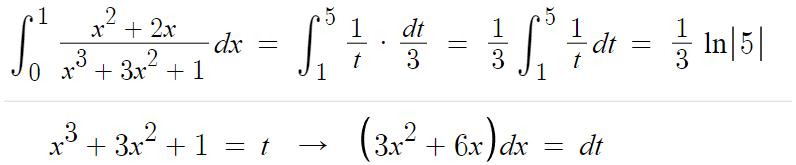
따라서 답은 3번
27 )

P의 위치는
y=x² 과 y = t²x - (lnt)/8 가 만나는 서로 다른 두 점의 중점이다.
만나는 두 점의 x좌표를 구한 뒤 그 두 점의 x좌표의 평균값을 구하면
거기가 중점이다.
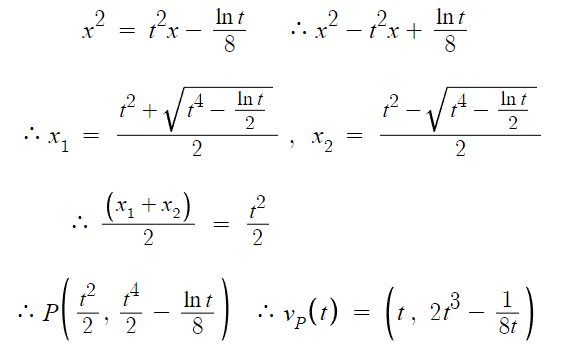
근과 계수의 관계 공식을 이용해서 바로 구할수도 있지만
최대한 정석적인 풀이를 위해 그렇게 하지는 않았다.
점 P의 위치와 속도를 알아냈으니
이제 이동거리를 구하기 위해
속도의 크기를 구한다음 적분하면 된다.
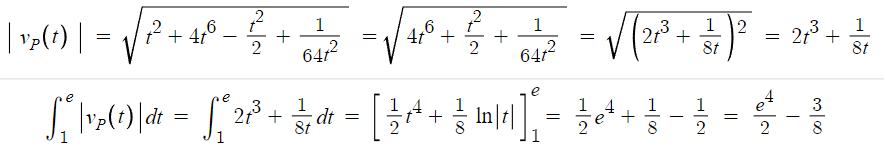
따라서 답은 1번
28 )

우선 g(x) = 3f(x) + 4cosf(x) 인데
f(x)는 이차함수이므로 실수 전체에서 미분 가능하다.
따라서 g(x)도 실수 전체에서 미분 가능하다.
그리고 f'(x)와 cosx는 실수 전체에서 미분 가능한 함수이다.
따라서 g'(x)도 실수 전체에서 미분 가능하다.
즉 g''(x)가 존재한다.
따라서 g(x)가 극소가 되는 x를 찾으라는건
g'(x) = 0 이면서
g''(x) > 0 인 지점을 찾으라는것
g'(x)와 g''(x)를 각각 구해보면

g(x)가 극소가 되려면
g'(x) = 0 이면서 g''(x)>0 이어야 하므로
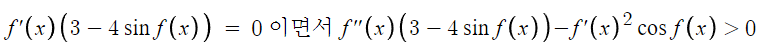
를 만족해야 한다.
g'(x)=0 이려면 f'(x)=0 이거나 sin( f(x) ) = 3/4 이어야 한다.
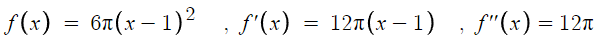
f(x), f'(x), f''(x)이 위와 같으므로
f'(x)=0 을 만족하는 x값은 x=1 하나 뿐이다.
sin( f(x) ) = 3/4 를 만족하는 x값은 꽤 많다.
어차피 개수만 세면 되기 때문에
이럴때 g''(x)>0 임을 보이기만 하면 된다.
우선 f'(x)=0 이라서 g'(x)=0인 경우
즉 x=1 인 경우를 보면
g''(x) = 12π( 3-4sin(f(x) ) > 0 을 만족해야한다.
따라서 sin( f(x) ) < 3/4 여야 한다.
x=1에서 f(x) = 0이므로 sin( f(x) ) = 0 이다.
따라서 조건을 만족하고 x=1은 극소점이다.
다음으로 sin( f(x) ) = 3/4 라서 g'(x)=0인 경우
이때도 g''(x) = -f'(x)²cos( f(x) ) > 0 을 만족해야한다.
우선 sin( f(x) ) = 3/4 일때 가능한 cos( f(x) )의 값은

만약 cos( f(x) ) 가 양수이면
g''(x) = -f'(x)²cos( f(x) ) > 0 을 만족하지 못한다.
따라서 g'(x)=0 이고 f'(x)≠0 일때 cos( f(x) ) 의 값은 다음과 같다.
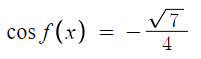
sin( f(x) ) 는 양수인데
cos( f(x) ) 는 음수이다.
이는 f(x) 값을 일반각으로 하는 동경이
제 2사분면에 위치한다는 뜻이다.
따라서 다음과 같은 결론을 얻는다.
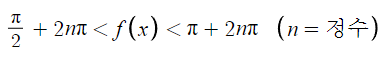
이걸 만족하면서 sin( f(x) ) = 3/4 면 g(x)는 극소이다.
이제 함수 f(x)의 그래프를
문제에서 준 범위 0<x<2 에서 그려보자.
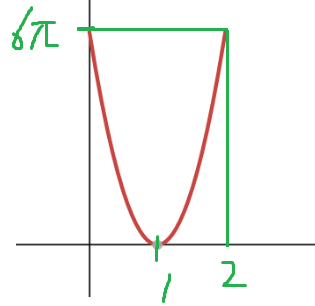
따라서 0 < f(x) < 6π 이다.
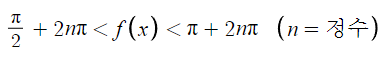
그 범위 내에서 이것과
sin( f(x) ) = 3/4 를 만족시키는 f(x)값은
π/2 와 π 사이에 하나
5π/2 와 3π 사이에 하나
9π/2 와 5π 사이에 하나
이렇게 있다.
각각의 f(x)값을 a, b, c 라 하겠다.
그러면 다음과 같이 된다.
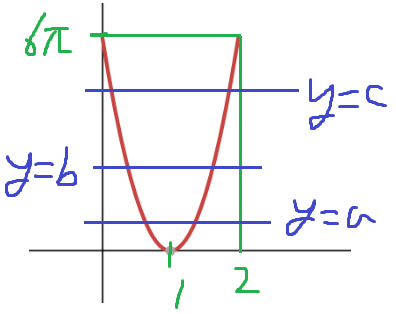
f(x)와 y=a, y=b, y=c 의 교점인 지점이 바로 g(x)가 극소가 되는 지점이다.

교점은 6개이고 따라서 이 경우 극소점은 6개이다.
여기에 마지막으로 x=1인 경우까지 더해주면
극소점은 총 7개이다.
따라서 답은 2번
29 )

1. f(θ)

빨간 부분의 넓이 + 녹색 부분의 넓이 - 파란색 부분의 넓이 = f(θ)
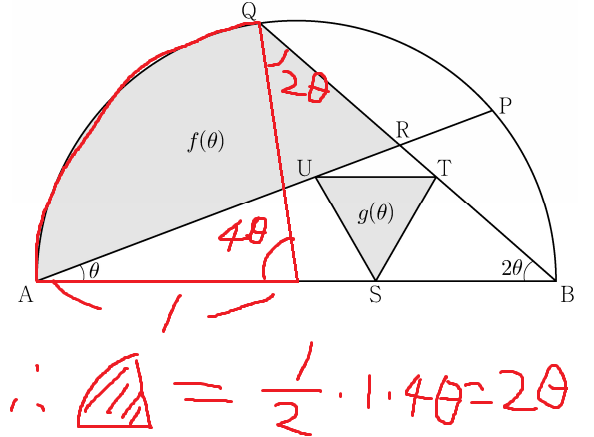

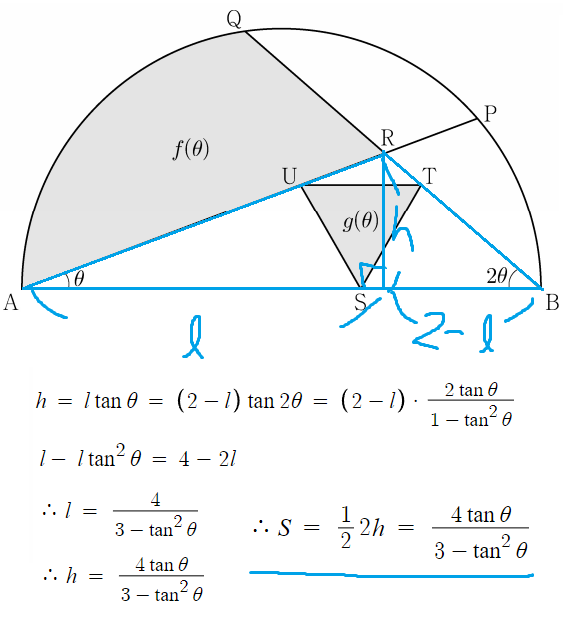
따라서 f(θ)는
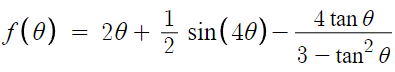
2. g(θ)
이제 g(θ) 를 구해볼건데
이 삼각형의 한 변의 길이를 a라고 하겠다.
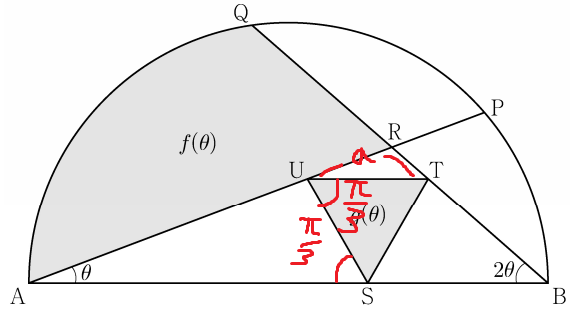
삼각형 STU가 정삼각형이므로 각 SUT는 π/3 이고
UT와 AB는 평행하기 때문에
각 ASU = 각 SUT = π/3 이다.
삼각형 ASU 에서 사인법칙을 적용하면
AU의 길이를 a와 θ로 나타낼 수 있다.
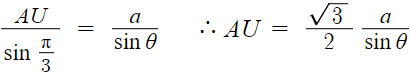
그리고 삼각형 RUT와
삼각형 RAB는 닮음이기 때문에
다음과 같은 비례식이 성립한다.
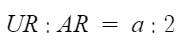
근데 아까 f(θ) 구할때 얻었던 정보를 이용하여
AR의 길이를 θ에 대해 나타낼 수 있다.
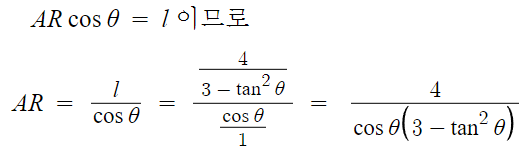
이 AR을 위 비례식에 넣고 정리하면
UR과 a, θ의 관계식이 나온다.
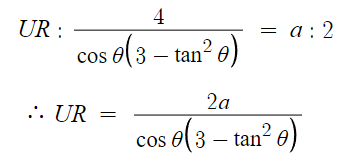
그 다음 AR = AU + UR 임을 이용하여 식을 정리하면
AR 알고 AU 알고 UR 아니까
a와 θ의 최종적인 관계식이 나온다.
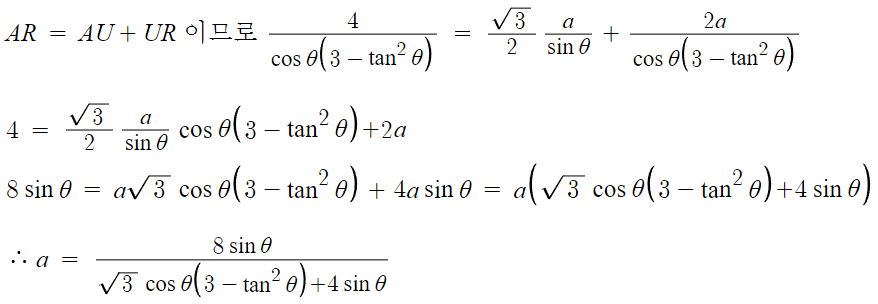
이제 마무리로 g(θ) 를 표현한 뒤 극한 계산하면 된다.
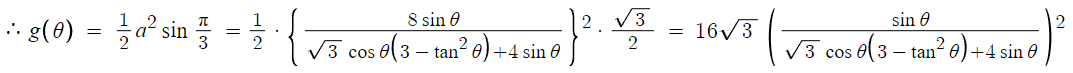
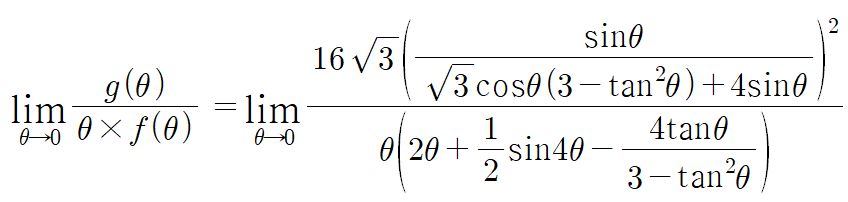
여기서 θ→0 일경우 극한값은 sinθ = tanθ = θ 이기 때문에
sinθ와 tanθ를 모두 θ로 바꿔서 푼다.
그리고 cosθ 의 극한값은 1이다.
분모에 cosθ-1=0 을 만드는 cosθ-1 같은 인수가 없기 때문에
cosθ를 1로 계산해도 극한값에는 영향을 끼치지 않는다.
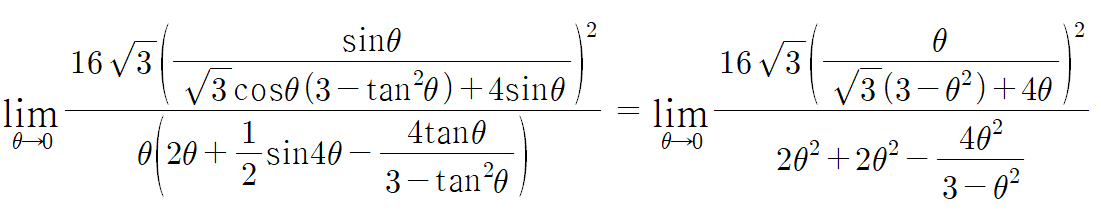
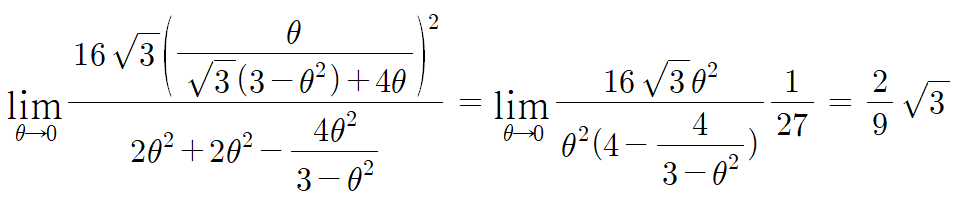
2+9=11
따라서 답은 11
30 )

당장 (가) 조건에서 크게 얻어갈건 없어보이고
(나) 조건부터 풀어보자.
(가) 조건에서 f(1)=1 이라 줬으니
x=1을 대입해보면
g(2) = 2f(1) = 2 이다.
따라서 g(2)=2 이고 f(2)=2 이다.
이번엔 x=2를 대입해보면
g(4) = 2f(2) = 4
따라서 g(4)=4이고 f(4)=4 이다.
이번엔 x=4를 대입해보면
g(8) = 2f(4) = 8
따라서 g(8)=8이고 f(8)=8이다.
이를 반복하면 다음과 같이 일반화된다.
x=2ⁿ(n은 자연수) 일 경우, g(x)=f(x)=x 이다.
이제 (가) 조건으로 돌아가면 저 정적분값이 무슨말인지 해석할수 있을거같다.
우선 아는대로 f(x)의 그래프를 그려보자면
f(1) = 1, f(2) = 2 이고 증가함수이므로
x=1과 x=2 사이에서는 이렇게 그려질것이다.
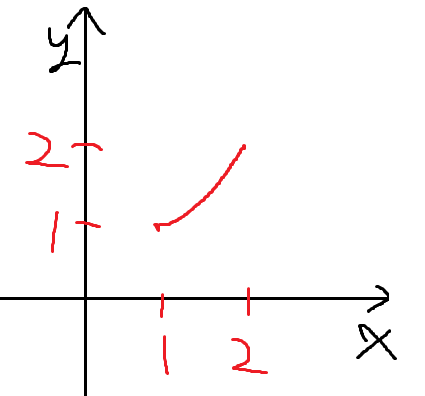
근데 여기서
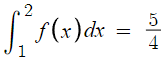
라고 한다.

파란색 부분의 넓이가 1이므로
녹색 부분의 넓이는 1/4 이다.
x=2ⁿ(n은 자연수) 일 경우, g(x)=f(x)=x 이다.
라는 조건에 의하면
x가 2의 배수일때가 특별한 지점이다.
첫번째 특별한 지점인 2는 했으니
이제 두번째 특별한 지점인 4를 해보자.
이번엔 x=2부터 x=4까지 그려보자.
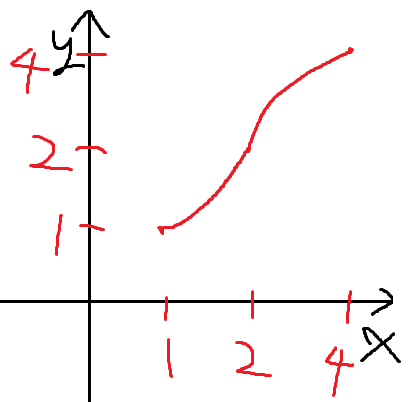
이런 느낌으로 그려질텐데
여기서 핵심은 (나) 조건에서 준 식이다.

따라서 아래 식이 성립한다.


g(x)의 x=2~x=4까지의 정적분의 의미는
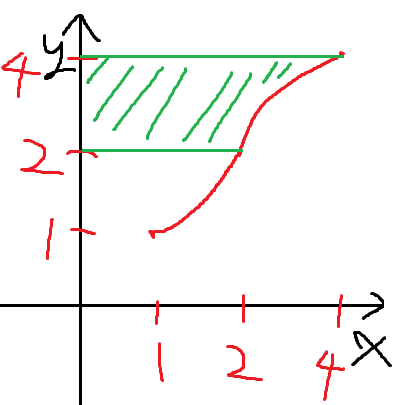
여기 색칠한 부분의 넓이가 5라는것이다.
왜 그런지 조금 설명해주자면
g(x)는 f(x)와 역함수이므로
f(x)와 y=x를 기준으로 대칭이다.
따라서 g(x)의 그래프를 그리고 싶다면
어렵게 생각할 필요 없이
그냥 x와 y를 바꿔주면 된다.
x와 y를 바꾸는 가장 쉬운 방법은

아까 그려놨던 이 f(x) 그래프에서
x축과 y축의 위치를 바꾸는거다.
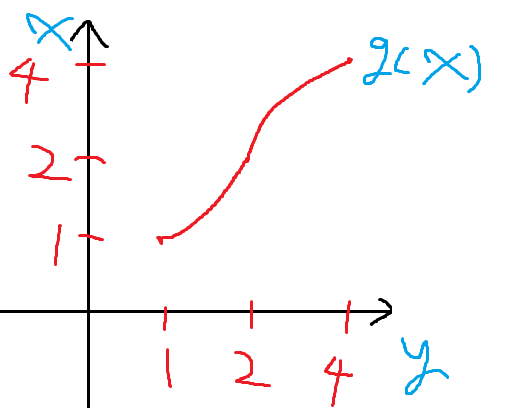
따라서 이게 g(x)의 그래프이다.
이걸 x=2부터 x=4까지 정적분하라 했으니까

결국 이부분의 넓이를 구한다는게 되는것이다.
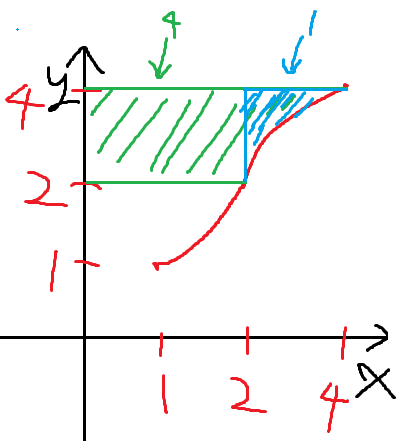
녹색으로 칠한 부분의 넓이가 4이므로
파란색으로 칠한 부분의 넓이는 1이다.
따라서 이를 이용해 f(x)의 x=2에서 x=4까지의 정적분 값을 알아낼 수 있다.
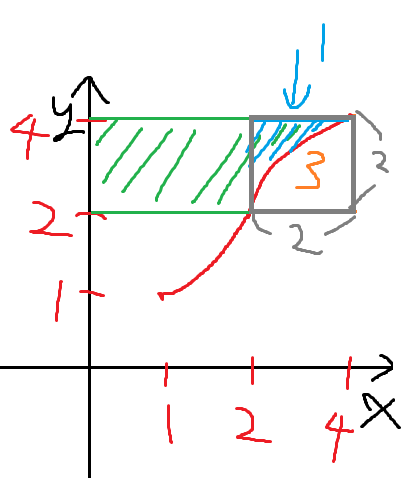
저 회색 네모친 부분의 넓이가 4니까
회색 네모친 부분 안에서
f(x)의 아래쪽 부분의 넓이는 3이다.
따라서 다음과 같은 결론을 얻을 수 있다.
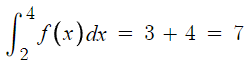
방금 한게 두번째 특별한 지점인 x=4 인 경우이고
세번째 특별한 지점인 x=8 에서도 해보자.
x=4부터 x=8 까지도 같은 방법으로 하면 된다.
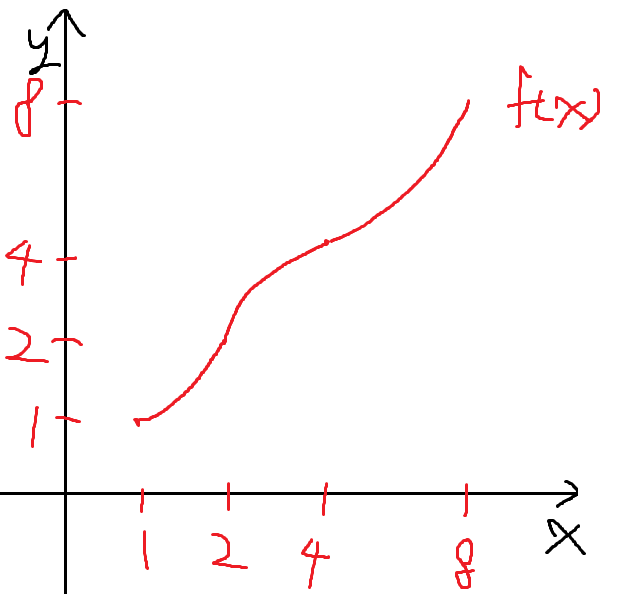
그림이 좀 깔끔하지 못한데 그냥 보자

따라서 아래 식이 성립한다.
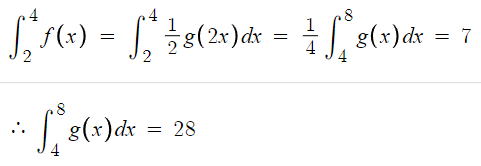
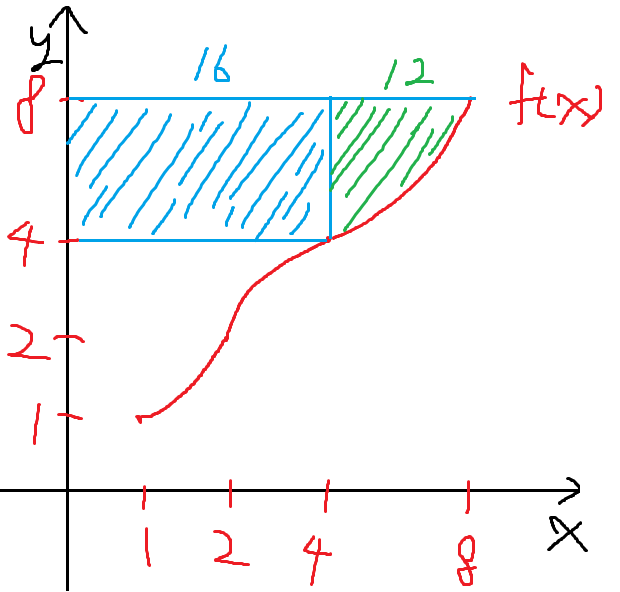
아까와 같은 논리로
녹색으로 칠한 부분은 12이고
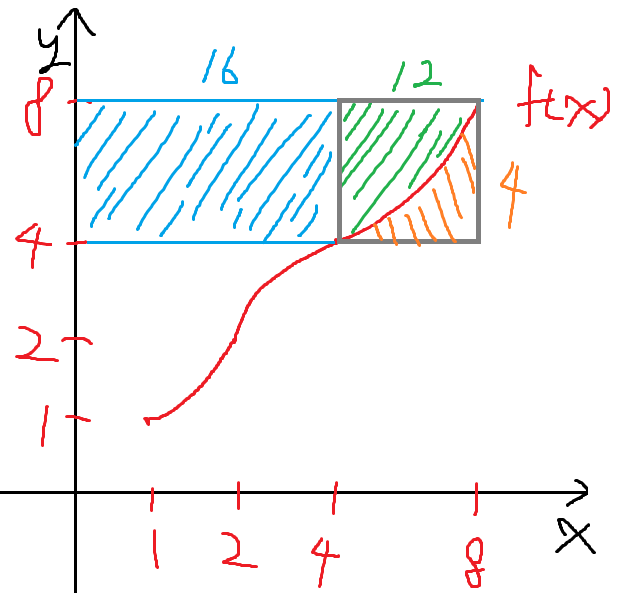
주황색으로 칠한 부분의 넓이는 4이다.
따라서 f(x)의 x=4부터 x=8까지의 정적분 값을 알아낼 수 있다.
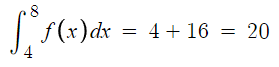
구하고자 하는건

이건데 f(x)의 정적분 값을 다 알았으니
이제 마무리하면 된다.
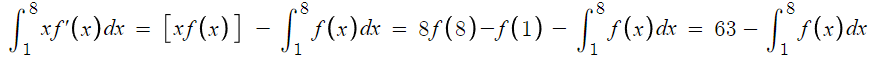
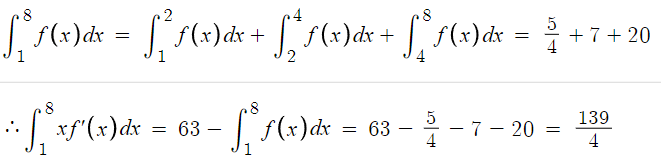
따라서 p+q = 4+139 = 143
따라서 답은 143
'2022학년도 기출 해설 > 2022학년도 수능 해설' 카테고리의 다른 글
| 2022학년도 수능 수학 확률과통계 23번~30번 해설 (1) | 2021.12.28 |
|---|---|
| 2022학년도 수능 물리II 해설 (0) | 2021.11.23 |
| 2022학년도 수능 물리I 해설 (0) | 2021.11.21 |
| 2022학년도 수능 수학 공통 16번~22번 해설 (0) | 2021.11.19 |
| 2022학년도 수능 수학 공통 1번~15번 해설 (0) | 2021.11.19 |



