
- 개요 -
수학(하)의 마지막 단원이 시작되었다.
마지막 단원은 '경우의 수' 에 관한 내용이다.
개념은 아주 쉬운곳이다.(상식적으로 쉽게 납득이 된다)
다만 말장난이 있고 헷갈릴만한 요소가 많기때문에
쉽다고 대충하기보단, '쉬워서 개념공부는 금방 끝나니
남는 시간에 문제를 많이 풀자' 라는 자세가 중요하다.
실제로 이 단원은 문제풀이가 핵심이다.
- 경우의 수란 무엇인가? -
경우의 수 : 한 번의 시행에서 일어날 수 있는 사건의 가짓수
말은 조금 어렵게 되어있는데, 예시를 들어보면 이해가 될것이다.
주사위 하나를 한 번 던진다고 해보자.
그럼 주사위에는
1의 눈이 나오는 사건
2의 눈이 나오는 사건
3의 눈이 나오는 사건
4의 눈이 나오는 사건
5의 눈이 나오는 사건
6의 눈이 나오는 사건
총 6가지의 '사건'이 일어날 수 있다.
따라서, 주사위 하나를 한 번 던질 때(한 번의 시행을 할 때)
총 6가지의 사건(사건의 가짓수는 6) 이 일어날 수 있으므로
주사위 하나를 던질 때 나오는 눈의 경우의 수는 6이다.
경우의 수는 어떻게 세는가?
그냥 나올 수 있는 사건들을 하나하나 세어봐야한다.
주사위의 눈이 6개라는걸 일일이 세봐서 알고있으니 경우의수가 6 이 나온거다.
하지만 이렇게 경우의 수를 하나하나 세서 구하는 방법은 곧 한계에 부딪힌다.
' 주사위 2개와 동전 2개를 동시에 던질 때 경우의 수는? '
이걸 하나하나 세서 구하기는 문제가 많다.
하나하나 센다고 치고 몇개 적어보겠다.
앞의 두개는 주사위의 눈의 수, 뒤의 두개는 동전의 앞면,뒷면 이다.
{1, 1, 앞면, 앞면}, {1, 1, 앞면, 뒷면}, {1, 1, 뒷면, 앞면}, {1, 1, 뒷면, 뒷면}
{1, 2, 앞면, 앞면}, {1, 2, 앞면, 뒷면}, {1, 2, 뒷면, 앞면}, {1, 2, 뒷면, 뒷면}
{1, 3, 앞면, 앞면}, {1, 3, 앞면, 뒷면}, {1, 3, 뒷면, 앞면}, {1, 3, 뒷면, 뒷면}
... 중간생략 ...
{6, 6, 앞면, 앞면}, {6, 6, 앞면, 뒷면}, {6, 6, 뒷면, 앞면}, {6, 6, 뒷면, 뒷면}
이걸 어느세월에 다 세나? 너무 많아서 곤란하다.
그나마 주사위2개 동전2개니까 좀 귀찮더라도 셀 수는 있었겠지만,
여기서 주사위와 동전이 10개씩만 되어도 도저히 셀 수 없는 지경에 이를것이다.
그래서, 경우의 수를 구하는 간편한 방법이 필요하다.
- 합의 법칙과 곱의 법칙 1 : 합의 법칙 -
그래서 경우의 수를 구하는 간편한 방법이 무엇인가?
그게 바로 '합의 법칙'과 '곱의 법칙' 이다.
경우의 수를 세는 데 있어서 무언가 법칙이 있고,
그걸 이용하면 경우의 수를 간단하게 구할 수 있다.
어떤 상황이든, 경우의수 계산은
합의법칙과 곱의법칙만을 이용하여 전부 해결할 수 있다.
이걸로 해결이 안 되면, 문제상황 해석을 잘못한 것이다.
물론 경우의 수는 '하나씩 세어보는 것'이 기본이며,
하나씩 세어보기에 너무 많다 싶으면, 합의 법칙과 곱의 법칙을 이용해서
계산을 간편하게 만들 수 있다는 것이다.
'법칙' 이라는 이름에 매료되어 기본을 잊지 말자.
합의 법칙 : 두 사건 A와 B에 대하여
사건 A와 B가 일어나는 경우의 수가 각각 m, n 일 때
A와 B가 한 번의 시행에서 둘다 일어나는게 불가능하다면
사건 A 또는 사건 B 가 일어나는 경우의 수는
둘의 경우의 수를 더해서 계산한다.
A 또는 B가 일어나는 경우의 수 = m+n
아마 긴가민가 할텐데, 예시를 들어보면 이해가 쉬울것이다.

이 문제를 같이 풀어보자.
1부터 50까지의 자연수가 각각 하나씩 적힌 카드가 총 50개 있다.
그 중 카드를 하나 뽑는다.
즉, '50개의 카드 중 하나를 뽑는다'는 '시행'을 '1회' 한다.
그 '한 번의 시행' 에서
'5의 배수'가 뽑히거나, '12의 배수'가 뽑히는
'경우의 수' 를 구해야한다.
'5의 배수가 뽑히는 사건'을 A,
'12의 배수가 뽑히는 사건'을 B
라 하겠다.
그럼, A 또는 B 가 일어나는 경우의 수를 구하는 문제가 된다.
A 또는 B? 합의법칙을 쓰고싶다는 생각이 든다.
A와 B가 둘다 일어날 수 있을까?
카드를 한개 뽑는데, 5의 배수이면서 12의 배수인 카드가 뽑힐 수 있을까?
그럴수 없다. 5와 12의 최소공배수는 60이기 때문에,
1부터 50까지의 자연수중 5와 12의 공배수는 존재하지 않는다.
따라서, 5의 배수이면서 12의 배수인 경우는 '불가능'하다.
따라서, 사건 A와 사건 B는 둘다 일어나는 게 불가능하고
따라서, A 또는 B가 일어나는 경우의 수는
합의 법칙을 적용하여 둘의 경우의 수를 더하면 된다.
A가 일어나는 경우의 수 = 5의 배수가 뽑히는 경우의 수 = 10
B가 일어나는 경우의 수 = 12의 배수가 뽑히는 경우의 수 = 4
따라서 A 또는 B가 일어나는 경우의 수는 10+4 = 14
따라서 답은 14
- 합의 법칙과 곱의 법칙 2 : 곱의 법칙 -
곱의 법칙 : 두 사건 A와 B에 대하여
사건 A와 B가 일어나는 경우의 수가 각각 m, n 일 때
A와 B가 한 번의 시행에서 둘다 일어난다면
사건 A와 사건 B가 둘다 일어나는 경우의 수는
둘의 경우의 수를 곱해서 계산한다.
A와 B가 둘다 일어나는 경우의 수 = m×n
이것도 문제로 예시를 들어보면 이해가 쉬울것이다.

이 문제를 같이 풀어보자.
한 개의 주사위를 두 번 던진다.
즉, '주사위를 두 번 던진다'는 '시행'을 '1회' 한다.
'주사위를 두번 던졌으니 시행은 2회 아닌가요?' 할 수 있는데
주사위를 두번 다 던지고 나서의 최종적인 결과에 대해
경우의 수를 구하라 하고 있으므로
'주사위를 두 번 던진다' 라는 것을 '한 번의 시행'으로 취급해야한다.
그리고, 이게 두 번의 시행이려면
첫번째 던지는 주사위와 두번째 던지는 주사위가 완전히 똑같은 경우여야한다.
여기서는 '첫번째' 주사위엔 '홀수의 눈이 나오는가?' 를 보라 하고,
'두번째' 주사위엔 '4의 약수의 눈이 나오는가?' 를 보라 했으니,
둘은 목적이 다르다. 따라서 첫번째와 두번째를 같다고 볼 수 없다.
따라서 두 번 던진다는것 자체를 '한 번의 시행' 으로 묶어서 생각해야 한다.
아무튼 문제풀이로 돌아가보자면
'주사위를 두 번 던진다'는 '시행'을 '1회' 할 때,
첫번째로 던진 주사위에선 홀수의 눈이 나오고,
두번째로 던진 주사위에선 4의 약수의 눈이 나오는
경우의 수를 구해야한다.
'첫번째로 던진 주사위에서 홀수의 눈이 나오는 사건'을 A,
'두번째로 던진 주사위에선 4의 약수의 눈이 나오는 사건'을 B
라 하겠다.
그럼, A와 B 가 둘다 일어나는 경우의 수를 구하는 문제가 된다.
A와 B가 둘다? 곱의법칙을 쓰고싶다는 생각이 든다.
A와 B가 둘다 일어날 수 있을까?
주사위를 두번 던지는데, 처음엔 홀수의 눈이 나오면서
두번째엔 4의 약수가 나올 수 있을까? 그럴수 있다.
따라서, A와 B가 둘다 일어나야하고,
이 때는 곱의 법칙을 적용하여 둘의 경우의 수를 곱하면 된다.
A가 일어나는 경우의 수 = 첫번째 던진것에서 홀수가 나오는 경우의 수 = 3
B가 일어나는 경우의 수 = 두번째 던진것에서 4의 약수가 나오는 경우의 수 = 3
따라서 A와 B가 둘다 일어나는 경우의 수는 3×3 = 9
따라서 답은 9
- 예제 -
1 )

'서로 다른' 이라는 생소한 표현 때문에 어려움을 느낄 수 있는데,
그냥 '주사위끼리, 동전끼리 구별이 가능하다'는 뜻이다.
주사위가 서로 색깔이 다르거나, 모양이 다른 상황 인거고
동전의 가격이 다른 상황인 것이다.
이에 대해서는 나중에 고3때 '확률과 통계' 에서 자세히 다룰 것이니
여기서는 무시하고 그냥 가자.
아무튼, 주사위 2개랑 동전 2개를 동시에 던질 때 경우의 수를 구해야한다.
주사위 두개의 이름을 각각 a, b
동전 두개의 이름을 각각 c, d
라고 하겠다. 구별을 위해서이다.
주사위 a에서 일어나는 사건을 A
주사위 b에서 일어나는 사건을 B
동전 c에서 일어나는 사건을 C
동전 d에서 일어나는 사건을 D
라 하겠다.
그런데, 주사위 2개와 동전 2개를 '동시에' 던진다고 했으므로
사건 A, B, C, D 는
'주사위 2개와 동전 2개를 던진다'는 '1회의 시행'에서
'네 사건이 모두' 일어나야 한다.
따라서, A와 B와 C와 D가 모두 일어나는 경우의 수를 구하면 되고,
'곱의 법칙'을 이용하면 될 것이다.
사건 A의 경우의수는 6
사건 B의 경우의수도 6
사건 C의 경우의수는 2
사건 D의 경우의수도 2
따라서, 최종적인 경우의 수는
6×6×2×2 = 144
따라서 답은 144 이다.
최대한 간단히 설명하자면,
주사위의 경우의수는 주사위하나당 6이고
동전의 경우의수는 동전하나당 2인데
주사위와 동전이 2개씩 있으니
6×6×2×2 = 144 라서 답은 144
2 )

'두 개의 주사위를 동시에 던진다' 는 '1회의 시행' 에서
'던져서 나오는 눈의 수의 합'을 보라고 한다.
눈의 수의 합이 4가 되거나, 7이 되어야 한다.
여기서 눈의 수의 합이 4가 되는 사건을 A,
눈의 수의 합이 7이 되는 사건을 B
라고 하겠다.
사건 A와 사건 B는 '한 번의 시행'에서 '둘다' 일어날 수 있는가?
그럴 수 없다. 눈의 수의 합이 4면서 7일수는 없기 때문이다.
따라서, 이 경우엔 '합의 법칙'을 적용해야 한다.
A와 B의 경우의 수를 각각 구한 뒤 더할것이다.
A의 경우의 수부터 구해보자.
이런건 나올 수 있는 경우가 많지 않으니, 하나씩 세어본다.
1+3=4, 3+1=4, 2+2=4 이므로
A의 경우의 수는 3이다.
B의 경우의 수 또한
나올 수 있는 경우가 많지 않으니, 하나씩 세어본다.
1+6=7, 6+1=7, 2+5=7, 5+2=7, 3+4=7, 4+3=7
이므로, B의 경우의 수는 6이다.
따라서, 최종적인 경우의 수는
A와 B의 경우의 수를 더한다.
(합의 법칙) 3+6 = 9
따라서 답은 9
3 )
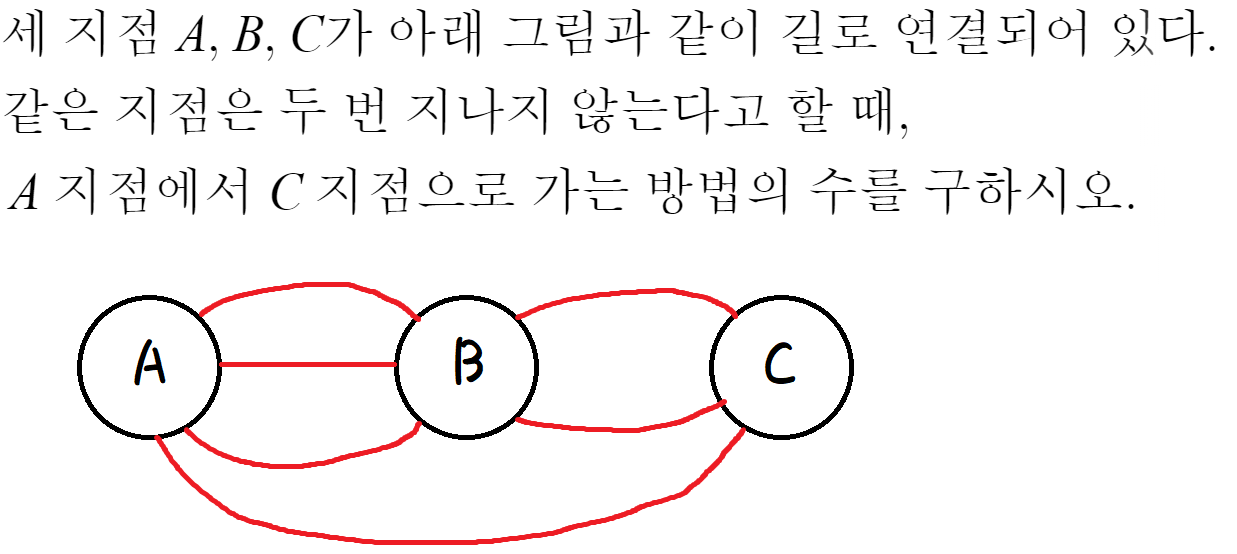
방법의 수 라는건 경우의 수 말하는거다.
그리고, 같은 지점은 두번 지나지 않는다는건
무조건 C를 향해 직진, 되돌아가지 않는다는거다.
만약 A에서 출발해서 B로 왔으면,
같은 지점을 두번 지나면 안되므로, 무조건 C로 가야한다.
목적은 A에서 C로 가는것이다.
B를 거쳐서 갈 수도 있고, B를 거치지 않고 갈 수도 있다.
그래서 나는 이 문제를 풀 때
B를 거쳐서 갈 때와, 거치지 않고 갈 때를 구분해서 구할것이다.
이렇게 구분하면,
B를 거쳐서 갈때와, 거치지 않고 갈때의 경우의 수를 각각 구한다음
그냥 둘을 더해주면 된다.
왜냐면, 'A에서 C로 간다'는 '1회의 시행' 에서
B를 거쳐서 C로 가는 사건과
B를 거치지 않고 C로 가는 사건은
'둘다 일어나는것이 불가능'하기 때문이다.
'합의 법칙'을 적용하기 위해 이렇게 경우를 나누는것이다.
1. B를 거치지 않고 가는 경우
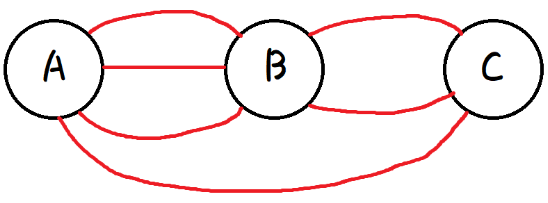
이 경우는 길이 하나밖에 없으므로 1이다.
2. B를 거쳐서 가는 경우

A에서 B로 가는 사건을 X
B에서 C로 가는 사건을 Y
라 하겠다.
그럼 X와 Y는 'A에서 C로 간다'는 '1회의 시행' 에서
'둘다' 일어나야 한다.
따라서, 이때 경우의 수는
X와 Y의 경우의수를 곱해서 계산해야한다.(곱의 법칙)
이걸 왜 또 X와 Y로 나눴느냐?
경우의 수는 최대한 많이 쪼개는게 계산을 줄이는 비법이다.
적게 쪼갤수록 '일일이 세어봐야 하는 경우의수'가 많아져서
경우의 수를 구하기 귀찮아진다.
물론 이 문제는 경우의수 자체가 작아서, 그냥 하나하나 세봐도 별 차이 없을거다.
X의 경우의 수는
A에서 B로 가는 길이 3개이므로 3이다.
Y의 경우의 수는
B에서 C로 가는 길이 2개이므로 2이다.
따라서, A에서 B를 거쳐서 C로 가는 경우의 수는
X와 Y가 일어나는 경우의 수 이며,
X의 경우의수가 3, Y의 경우의수가 2 이므로
최종적으로 3×2 = 6 이다.
3. 마무리계산
(B를 거쳐가는 경우의 수) + (B를 안거쳐가는 경우의 수)
=
1 + 6 = 7
따라서 답은 7이다.
하나씩 세어보는것도 좋은 방법이다. 직접 해보기 바란다.
4 )

순서쌍 (x, y, z)의 개수를 구하라는 건
저 방정식을 만족하는 (x, y, z)의 경우의 수를 구하라는것
경우의 수를 구하는 기본 : '일일이 세어 본다'
기본을 잊으면 이 문제를 풀 수 없다.
x, y, z는 셋다 자연수이므로 하나씩 세어봐도 크게 무리가 없다.
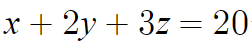
x의 계수는 1, y의 계수는 2, z의 계수는 3이다.
어차피 하나씩 세어볼거지만,
x, y, z중 뭘 기준으로 잡고 세는게 쉬울까?
x, y, z는 전부 자연수니까
1, 2, 3, 4, 5... 하나씩 대입해서 본다고 치면
z를 기준으로 잡는게 쉬울것이다.
왜냐면 x는 1, 2, 3, ... 이런식으로 1씩 커질거고
2y는 2, 4, 6, ... 이런식으로 2씩 커질거고
3z는 3, 6, 9, ... 이런식으로 3씩 커질거기 때문에
계수가 가장 큰 z를 기준으로 잡는게 경우를 나눌 게 적어져서
경우의 수를 하나씩 셀때 가장 수월할것이다.
물론 x를 기준으로 잡고싶으면 그래도 된다.
1. z=1인 경우
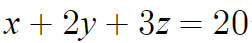
x+2y+3z=20 에서 z=1 대입하면
x+2y = 17 이다.
여기서도 결국 이를 만족하는 x, y를 하나하나 셀거지만
이것 또한 문제 상황을 분석해서 번거로운 과정을 줄일 수 있다.
왜냐면, y는 자연수기때문에 2y는 짝수이다.
x+짝수 = 17(홀수) 이므로
x는 홀수여야한다.
이것들을 토대로 하나씩 세어보자면,
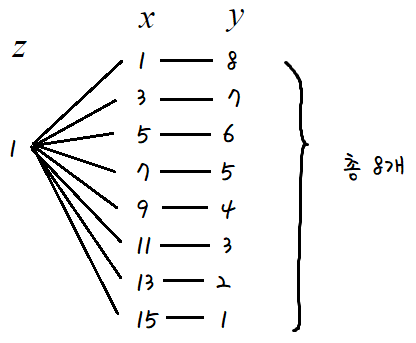
따라서 z=1 인 경우의수는 8이다.
추가로, 경우의 수를 셀 때 저렇게 그려진 것을 '수형도'라 한다.
하나하나 세는 과정을 전부 암산으로 처리하기는 어려우니
저렇게 한 눈에 잘 보이게 그려서 분석하라는 것이다.
수형도를 꼭 써야하는 건 당연히 아니고,
나름의 꿀팁을 줄테니 알아서 취향껏 하라는 뜻이다.
어차피 어떤 방법이든 답만 내면 그만이다.
2. z=2인 경우
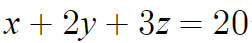
이때는 x+2y = 14가 되고
아까랑 똑같은 논리로 2y는 짝수인데
x+2y=14(짝수) 이므로, x는 짝수이다.
이를 토대로 수형도를 그리면

따라서 z=2 인 경우의수는 6이다.
3. z=3인 경우
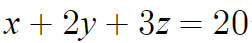
이때는 x+2y = 11이 되고
같은 논리로, x는 홀수이다.
이를 토대로 수형도를 그리면
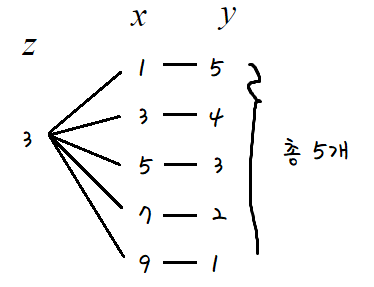
이쯤 오면 나름의 규칙을 찾았을테니 금방 할것이다.
따라서 z=3 인 경우의수는 5이다.
4. z=4인 경우
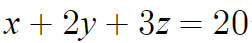
이때는 x+2y = 8이 되고
같은 논리로, x는 짝수이다.
이 때는 수형도를 생략하겠다.
굳이 안 그려봐도 될 정도로 경우가 몇 없다.
가능한 (x, y)는 (2, 3), (4, 2), (5, 1) 로 총 3개이다.
따라서 z=4 인 경우의수는 3이다.
5. z=5인 경우
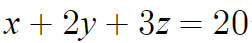
이때는 x+2y = 5 이고
가능한 (x, y)는 (1, 2), (3, 1)로 2개이다.
따라서 z=5 인 경우의수는 2이다.
6. z=6인 경우
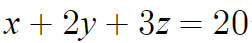
이때는 x+2y = 2 이고
이를 만족하는 자연수 x, y는 존재하지 않는다.
따라서 z=6인 경우의수는 0이다.
7. z>6인 경우?
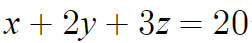
z가 커질수록 x+2y+3z의 값도 커지므로,
이 이상은 해볼 필요도 없이 경우의수 0이다.
8. 마무리 계산
z=1인 경우의수
z=2인 경우의수
z=3인 경우의수
z=4인 경우의수
z=5인 경우의수
이것들은 서로 더해야할까 곱해야할까?
'합의법칙', '곱의법칙' 중 무엇을 써야할까?
(x, y, z) 순서쌍을 만든다는 '1회의 시행'에서
z값은 하나로 꼭 정해져야만 한다.
따라서, 1회의 시행에서 z=1 이면서 z=2 인 경우는 불가능하고
따라서 이때는 합의법칙을 적용해야한다.
z=1인 경우의수 + z=2인 경우의수 + z=3인 경우의수
+ z=4인 경우의수 + z=5인 경우의수
= 8 + 6 + 5 + 3 + 2 = 24
따라서 답은 24
'수학(하) > III. 순열과 조합' 카테고리의 다른 글
| 조합 #1 - 조합이란? (0) | 2022.10.09 |
|---|---|
| 순열 #2 - 순열 문제풀이 (0) | 2022.08.28 |
| 순열 #1 - 순열의 뜻과 계산 (0) | 2022.08.24 |


