
- 개요 -
곱의 법칙의 심화과정이다.
곱의 법칙을 소홀히 했다면 여기가 어렵게 느껴질것이다.
- 조합이란? -
한 줄로 요약하자면,
조합 : 전체 중 일부를 뽑는것(나열하지 않음)
정확한 뜻은 이렇다.

'순서를 생각하지 않고' 라는 표현이 조합의 핵심이다.
n개 중 r개를 뽑는 시행
그게 조합이다.
뽑아서 나열까지 하면 그건 순열이다.
n개 '중에서' 뽑는 것이므로,
r은 n보다 커질 수 없고 1보다 작을수도 없다.
그러면 그렇게 나열된 것은
무엇을 뽑느냐에 따라서
여러가지가 나오게 될 것이다.
즉, 조합은 한두개가 아니다.
이 때, 이러한 조합의 수를 기호로 ₙCᵣ 로 나타낸다.
쉽게 말해서 ₙCᵣ은 '조합의 경우의 수' 이다.
추가로, 기호로 C를 쓰는 이유는
조합이 영어로 Combination 이라서 앞 글자 따온것이다.
- 조합의 수 기본 계산법 -
직접 간단한 것부터 해보겠다.

이걸 구해보겠다.
저것의 뜻은,
서로 다른 5개 중 3개를 뽑는 방법의 수
즉, 조합의 수
이 문제에서 준 조합 = '5개중 3개를 뽑는다'는 '시행'
따라서, 5개 중 3개를 뽑는(고르는) 경우의 수를 구해야 한다.
그런데 좀 의아하지 않은가?
뽑고 나서 나열까지 하는게 순열이었고,
그럼 나열까지 하는게 더 어려울텐데
왜 굳이 조합이 순열 뒤쪽 내용으로 배치되었는지 말이다.
조합의 수는 순열의 수를 이용해 계산하기 때문이다.
따라서, 뽑기만 하는게 오히려 더 어렵다.
순열의 수를 이용한다는게 무슨 말인가?
일단 순열의 수를 구해보겠다.

순열의 수는 60이다.
순열이 뭐였는지 상기해보자.
'뽑고, 나열한다.'
그럼 우린 어떻게 할 것이냐?
일단 뽑고 나열하는 경우의 수는
순열의 수이므로, 쉽게 계산할 수 있다.
그럼 일단 순열의 수를 구한 뒤,
나열하는 경우의 수를 나눠주면 되는것이다.

이것만으로는 이해가 안 될수 있다고 생각하므로,
더 쉬운 상황으로 예를 들어주겠다.

2개 중 2개를 택하는 조합의 수(경우의 수)는 몇인가?

A와 B가 있다고 하고,
이 2개의 알파벳 중 2개를 뽑는 경우의 수
당연히 둘 다 뽑는(선택하는) 경우 하나밖에 없으니
답은 1이다.
그럼 이게 왜 (순열의 수) / (뽑힌 2개를 나열하는 경우의 수)
가 되어야 하는지 설명해주겠다.
일단 하나씩 뽑을거다.
즉, 첫번째에 하나 뽑고
두번째에 나머지 하나를 뽑을것이다.
첫번째에 뽑을 수 있는 알파벳은 A 또는 B로, 2개이다.
두번째에 뽑을 수 있는 알파벳은, 남은게 하나니 그냥 1개이다.
분명 뽑으래서 뽑았는데 경우의수가 2인 것처럼 보인다.
왜 이런 일이 벌어졌느냐?
하나씩 뽑는 과정 자체가 나열이기 때문이다.
하나씩 뽑는다는건, 순서대로 뽑겠다는것이다.
어차피 결과적으로 A가 선택되어야 하는데,
첫 번째에 A를 뽑나, 두 번째에 A를 뽑나
사실 뽑기만 하는게 조합이기 때문에
이 둘은 하나의 경우의 수(다른 경우로 취급하지 말자는 뜻)로 취급해야한다.
그런데, 우리는 A와 B중 하나를 골라서 하나씩 뽑았으니,
A가 뽑힌다. 라는 하나의 경우에
A가 첫번째로 뽑히는 경우와 두번째로 뽑히는 경우
이렇게 두 가지의 경우가 나오게 되는 것이다.
첫번째로 뽑힌 A, 두번째로 뽑힌 A
하나씩 뽑는다는 것 자체로, 뽑힌것들에 순서가 부여되는 것이다.
뽑은걸 나열하려고 까지는 하지 않았는데, 원치 않게 나열까지 해버린 것이다.
그래서, 뽑는 과정에서 어쩔 수 없이 나열된걸
다시 초기화해줘야 한다는 것이다.
그래서, A가 첫번째에 뽑혔는지 두번째에 뽑혔는지는
뽑는 입장에서는 관심사가 아니므로,
A와 B가 뽑히는 순서에서 나오는 경우의 수인 2를
최종적으로 나누어줘야 우리가 원하는 조합의 수가 나오는것이다.

내 예상보다 글이 길어졌으니,
가볍게 조합 계산 하나만 하고 넘어가자.
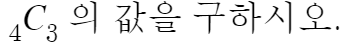
문제 해석 : 4개 중 3개를 선택하는 방법의 수는?
일단 순서대로 하나씩 3번 뽑은 다음,
이렇게 뽑힌 3개가 원치 않게 이미 나열되어있으니
3개를 나열하는 경우의 수인 3!을 나눈다.

따라서 답은 4이다.
- 조합의 수의 일반화(공식) -
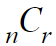
이걸 구해보자.
서로 다른 n개 중 r개를 뽑는 경우의 수는?
일단 r개를 뽑아서 나열한 뒤,
r개를 나열하는 경우의 수로 나눈다.
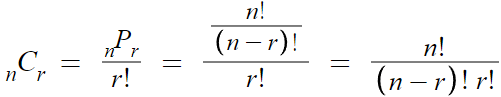
공식은 꽤 복잡해보이지만,
순열의 수만 구할 수 있다면 무리없이 계산 가능하니
무작정 외우려 들 필요는 없다.
'경우의 수' 문제를 잘 푸는 방법은
'공식에 너무 의존하지 않는 것' 이다.
- 조합의 수의 성질 -
1. 서로 다른 n개 중 n개를 뽑는 경우의 수는 1이다.
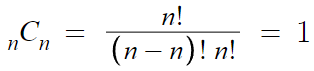
공식에 대입해봐도 그렇고, 상식적으로도 당연하다.
2. 서로 다른 n개 중 0개를 뽑는 경우의 수는 1이다.
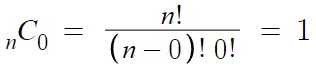
0개를 뽑는다는건, 아무것도 하지 않겠다는것
아무것도 하지 않는 경우 하나밖에 없으므로, 경우의 수는 1이다.
3. 서로 다른 n개 중 r개를 뽑는 경우의 수와
서로 다른 n개 중 n-r 개를 뽑는 경우의 수는
항상 같다. (중요)
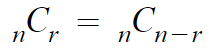
순열엔 없고, 조합에서만 볼 수 있는 성질이다.
수식으로도 증명할 수 있고, 직관을 이용해 증명할 수도 있다.
둘 다 보여주겠다.

공식에 대입해보면, 둘은 같다는 것을 알 수 있다.
직관적으로 설명해주자면,
n개 중 r개를 뽑는 건
n개 중 n-r 개를 뽑지 않는다는 것과 같다.
즉, 뽑을 r개를 선택한다는건
뽑지 않을 n-r 개를 선택한다는 것과 같다.
활용 예시를 하나 보여주겠다.
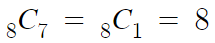
8개중 7개를 선택한다는 것은,
뽑지 않을 1개를 선택한다는 것과 같은 말이다.
8C1을 계산하는게 더 쉬우니까 이렇게 바꾸는것이다.
설마 이것도 공식에 대입하려 하지는 않겠지?
8C1의 의미를 생각해보자.
8개 중 1개를 선택하는 경우의 수
그럼 8개중 하나만 택하는거니 당연히 경우의수는 8이다..
- 예제 -
1 )

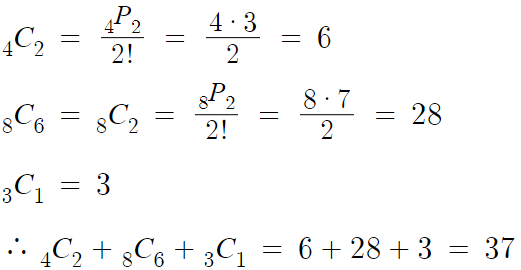
따라서 답은 37
2 )

그냥 공식에 대입해서 만족하는 k값 찾으면 되는거다.
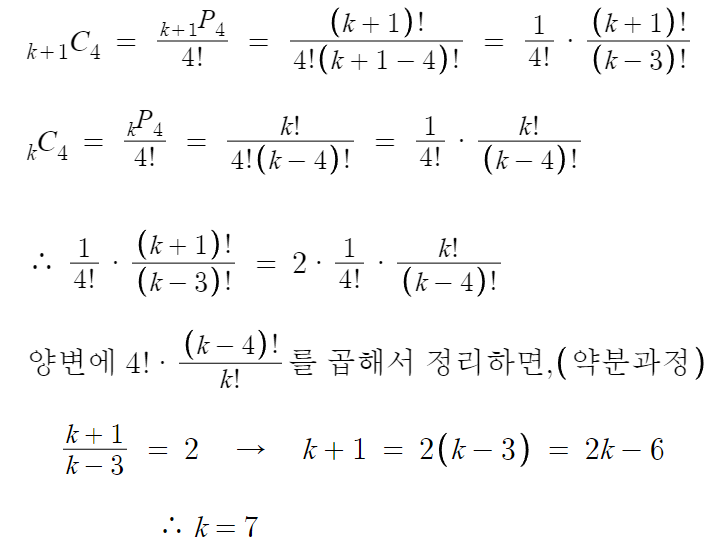
따라서 답은 7
3 )

어려워 보이겠지만, 사실 그냥 팩토리얼(계승) 가지고 식조작 좀 해주면 끝난다.
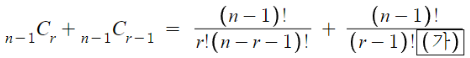
맨 윗줄의 이 식은
그냥 조합의 수 공식을 쓴것 뿐이다.
따라서 (가)에 들어갈 것은 { (n-1) - (r-1) } ! = (n-r)! 이다.
이어서, 이걸 이용해 (나)에 들어갈 것을 찾아보자.
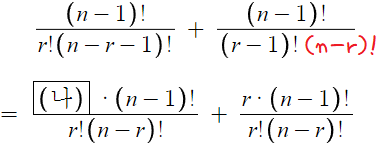
이 과정에서 무슨 일이 일어났는가?
왼쪽의 분수식을 보면, 분모에 n-r 이 곱해져있는 상태이고
오른쪽의 분수식을 보면, 분모분자에 똑같이 r이 곱해져있는 상태이다.
따라서, 등식이 그대로 성립하려면
왼쪽의 분수식에서 분자 역시 n-r이 곱해져있어야한다.
따라서 (나)에 들어갈 것은 n-r 이다.
마지막으로 (다)

증명의 마지막 줄에 있는걸 쓴거다.
이건 조합의 수 공식을 쓰면 금방 구할 수 있다.
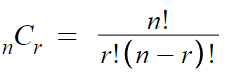
따라서, (다)에 들어갈 것은 n! 이다.
따라서 답은
(가) : (n-r)!
(나) : n-r
(다) : n!
4 )

1 )
모든 방법의 수는
곧 서로 다른 5개 중 3개를 선택하는 경우의 수
즉 5개중 3개를 선택하는 조합의 수를 의미한다.
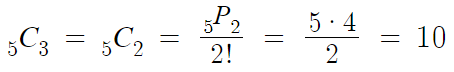
따라서 답은 10
2 )
A는 선택하고, B는 선택하지 않는다?
이러면 오히려 쉬운 상황이 되는데,
그림으로 나타내자면 이렇게 된거다.

따라서, A는 이미 뽑기로 했으니
나머지 2개 뽑을것을
C, D, E 중 선택해주면 된다.
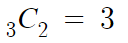
따라서 답은 3
'수학(하) > III. 순열과 조합' 카테고리의 다른 글
| 순열 #2 - 순열 문제풀이 (0) | 2022.08.28 |
|---|---|
| 순열 #1 - 순열의 뜻과 계산 (0) | 2022.08.24 |
| 경우의 수 : 합의 법칙과 곱의 법칙 (0) | 2022.08.20 |


