천체의 운동을 기술하는게 케플러 법칙이다.
뉴턴과 케플러의 합작이다.
- 케플러 제1법칙 -
타원 궤도 법칙이라고도 한다.
행성은 태양을 하나의 초점으로하는
'타원 궤도'를 따라 운동한다.

타원의 정의 : 평면 위의 두 점에서의 거리의 합이 일정한 점들의 집합으로 만들어지는 곡선
이때 이 두 점을 초점이라한다.
즉 p+q는 항상 일정하다.
행성이 태양을 초점으로하는 타원 궤도를 따라 돈다는것이다.
여기서 태양과 가장 가까운 지점을 근일점
가장 먼 지점을 원일점이라 한다.
- 케플러 제2법칙 -
면적 속도 일정 법칙 이라고도 한다.

행성과 태양을 연결하는 선은
같은 시간 동안 같은 면적을 쓸고 지나간다.
이에 따라
근일점에 가까워질수록
태양과 행성을 연결하는 선의 길이가 짧아질것이므로
이 법칙을 만족하기 위해
근일점에 가까워질수록 속력이 빨라져야한다.
즉 r₁ > r₂ 라면 v₁ < v₂ 이다.
- 케플러 제3법칙 -
조화 법칙 또는 주기의 법칙 이라고도 한다.

행성의 공전 주기 T의 제곱은
타원 궤도의 긴반지름 a의 세제곱에 비례한다.

양변에 제곱근을 취하면

이렇게 표현할수도 있다.
문제 풀때는 아래 식이 더 빨리풀린다.
행성 A는 긴반지름 a로 돌고있고
행성 B는 긴반지름 2a로 돌고있다.
A와 B의 주기의 비는?
긴반지름의 비가 1 : 2 니까
주기의 제곱의 비는
긴반지름의 세제곱의 비인 1 : 8과 같고
따라서 주기의 비는 1 : 2sqrt(2) 이다.
아래 식에다가 그냥 집어넣으면 더 빨리 풀수있다.
주기의 비는 a sqrt(a) : 2a sqrt(2a)
따라서 1 : 2sqrt(2)
즉, 태양에서부터 멀리 있는 행성일수록
공전 주기가 길다.
- 만유인력의 법칙 -
뉴턴 중력 법칙이라고도 한다.
질량을 가진 두 물체 사이에는
서로 잡아당기는 힘이 작용하며,
이 힘의 크기는
두 물체의 질량의 곱에 비례하고
거리의 제곱에 반비례한다.


저 식에서 G는 만유인력 상수 이다.
- 만유인력과 케플러 법칙의 관계 -
태양계의 행성들이
태양을 초점으로 공전할 수 있는 이유가 뭘까?
태양과 행성 사이에 작용하는 만유인력이
구심력 역할을 한 것이다.
태양계의 행성들은
타원 궤도를 운동하지만 거의 원궤도에 가깝다.
따라서 원 궤도라 가정하고
만유인력 법칙을 구심력이라 하면
케플러 제3법칙을 유도할 수 있다.

원도 타원이기 때문에
여기다가 케플러1법칙을 개입시키면
행성이 긴반지름 r인 타원궤도로 공전한다고 보면 된다.
모든 원은 타원이지만,
모든 타원은 원이다. 라는건 성립하지 않기때문에
타원에다가 원의 구심력 식을 개입시키면 안된다.
라는 것만 주의하면 된다.
- 심화 1 : 궤도반지름이 다른 천체의 속력 비교 -

두 천체 A와 B는
행성을 초점으로 하는 궤도로 공전중이다.
A와 B는 둘다 r점을 지나며,
A는 원운동하고, B는 r점이 원일점이다.
이때 r점에서 A와 B의 속력을 비교해보자.
A가 원 궤도를 따라 운동할 수 있는 이유는
행성이 A를 당기는 '만유인력'이
완벽히 '구심력' 의 역할을 해냈기 때문이다.
즉 만유인력=구심력 이면 원운동한다.
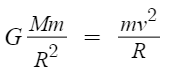
양변의 공통 인수 m/R을 없애기 위해
R/m을 곱한 뒤 정리하면 다음과 같이 된다.

따라서 이게 A의 r점에서의 속력이다.
다음으로 B를 보면
B는 r점을 지난 후 행성과 가까워진다.
원운동하지 않은것이다.
왜 원운동하지 않았냐면
행성이 B를 당기는 '만유인력'이
원운동을 하는 '구심력'의 역할을 하기에는
크기가 너무 크거나 작았다는 것이다.
여기서는 r점을 지난 후 행성과 가까워지므로
만유인력이 구심력의 역할을 하기에는 크기가 너무 컸다는 결론에 다다르게 된다.
즉 만유인력>구심력 이다.
따라서 아래 식이 성립한다.

이것도 v_b만 남기고 정리하면

이렇게 된다.
따라서 r점에서의 속력은 A가 B보다 빠르다.
만약 B의 운동 궤도에서
r점이 원일점이 아니라 근일점이었다면?
그러면 B는 r점을 지난 후 행성과 멀어질것이다.
행성과 멀어진다는건
행성이 B를 당기는 '만유인력'이
B를 원운동시킬 '구심력' 의 역할을 하기에는 너무 작았던것이다.
즉 이때는 만유인력<구심력 이다.

따라서 이 경우 r점에서의 속력은 B가 A보다 빠르다.
- 심화 2 : 역학적 에너지 -
타원궤도로 운동하는 천체의 역학적에너지는 보존되는가?
답은 '그렇다' 이다.
각 천체가 어떤 행성이나 항성을 초점으로 하는 타원궤도로 운동할텐데
이때 문제 상황이 너무 복잡해지게하지 않기 위해
문제에서 제시하는 조건에서
각 천체에 작용하는 힘은
천체와 행성 사이의 만유인력 뿐이다. 라고 알려주기 때문이다.
즉 천체에 작용하는 힘은 '만유인력' 하나 뿐이다.
만유인력은 곧 중력(보존력)이고
보존력만이 작용하는 운동이므로
역학적에너지는 보존된다.
- 이심률 -
중요한건 아니라서 한번 슥 읽어보면 된다.
타원이 찌그러진 정도를 나타낸다.

수식은 이렇다.
a는 긴반지름, b는 짧은반지름이다.
원은 긴반지름=짧은반지름 이기 때문에
이심률이 0이다.
즉 이심률이 0에 가까울수록 원에 가깝다.
- 제 1 우주속도 -
인공위성이 지구 주위를 등속 원운동 하기 위한 속력을
제 1 우주속도라고 한다.
아까 심화 1 에서 다루었던 내용과 관련이 깊은 곳이다.
인공위성이 지구 주위를 제 1 우주속도로 운동한다면
지구가 인공위성을 당기는 '만유인력'이 '구심력'의 역할을 완벽히 해낸다는것이다.
이것도 중요한거 아니니까 한번 슥 읽어보자.

- 제 2 우주속도 -
탈출 속도라고도 한다.
말 그대로 천체의 인력을 벗어나 탈출하기 위한
'최소한'의 발사 속도이다.
유도를 해주긴 할텐데 사실 필요없고
식만 외워가면 된다.
발사된 물체가 그 천체와의 만유인력만을 받는다고 가정하면,
물체의 역학적에너지는 보존된다.
지구를 예로 들어서 지구 탈출 속도를 구해보자.
지구가 잡아당기는 중력만 있다고 해보자.
그럼 역학적에너지는 보존된다.
근데 이때의 속도는
지구의 중력장을 벗어나기 위한
'최소한'의 속도 이고
중력장의 범위는 무한이기 때문에
중력장을 벗어나기 위한 최소한의 속도
즉 중력장을 간신히 벗어나는 속도는
지구의 중력장을 간신히 벗어나는
지구와 무한대로 떨어진 거리에서
운동에너지가 0이라는 말이다.


이 식만 외우면 된다.
R : 천체의 반지름
G : 만유인력 상수
M : 천체의 질량
- 예제 -
1 )

철수)
케플러 제1법칙 : 행성은 타원 궤도 운동을 한다.
따라서 철수(o)
영희)
누구나 아는 상식인데
만유인력은 뉴턴이 발견한거다.
따라서 영희(o)
민수)
사과가 땅에 떨어지는건
땅과 사과가 서로 당기는
만유인력 때문이라고 설명할 수 있다.
따라서 민수(o)
따라서 답은 5번
2 )


따라서 답은 4번
3 )

ㄱ)
태양과의 거리는
a에서가 b에서보다 가까우므로
케플러 제2법칙을 만족하기 위해서는
a에서의 속력이 b에서보다 커야한다.
따라서 ㄱ(x)
ㄴ)
태양과의 거리는
a에서가 c에서보다 가깝고
만유인력은 거리의 제곱에 반비례하므로
거리가 가까운 a가 더 큰 만유인력을 받을것이고
F = ma = GMm/r² 라서
어차피 m은 약분된다.
따라서 가속도의 크기는 a에서가 c보다 크다.
따라서 ㄴ(o)
ㄷ)
a에서 b까지 운동하는 시간과
b에서 c까지 운동하는 시간이 같다 했으므로
케플러 제2법칙에 의해
a에서 b까지 운동할때 만드는 면적과
b에서 c까지 운동할때 만드는 면적이 같다.
S₁이 S₂의 2배라 했으므로
S₁ = S 라 하면
S₂ = 2S고
a→b 에서 만드는 면적은 S₂와 같은 2S이다.
따라서 행성의 한 공전주기 동안 만드는 면적이
S + 2S + 2S = 5S 라는거고
따라서 b에서 c까지 운동할때 2S면적 만들었으니
운동시간은 2/5 주기만큼 이다.
따라서 ㄷ(o)
따라서 답은 4번
4 )


이 식을 이해하고 있는가가 핵심이다.
ㄱ)
P와 Q에 작용하는 만유인력의 크기가 같은 지점은
만유인력의 크기가 2F0_ 인 지점이다.
만유인력의 크기가 같은데
거리는 sqrt(2) 배이다.
만유인력의 크기는
거리의 제곱에 반비례하므로
m1 : m2 = 1 : 2 이다.
공식 써서 풀어도 된다.

따라서 ㄱ(x)
ㄴ)
거리가 최대일때 만유인력은 최소일것이다.
Q에서 만유인력의 최솟값은 F0_이고
2F0_에서 거리가 sqrt(2)r0_ 이다.
만유인력이 2 : 1이니 거리는 1 : sqrt(2)이다.
따라서 F0_에서 거리는 sqrt(2)*sqrt(2)*r0_ = 2r0_이다.
수식으로 풀어도 된다.

따라서 ㄴ(o)
ㄷ)
공전 주기를 구하려면
타원 궤도의 긴반지름을 알아야하고
그 긴반지름을 알기 위한 힌트가
거리와 만유인력의 크기와의 관계이다.
ㄴ 풀때와 같은 방식으로
P와 Q가 각각
만유인력이 최대일때 거리와
최소일때 거리를 저 그래프에 채워보겠다.

Q의 공전주기가 P의 2sqrt(2)배가 되려면
케플러 제3법칙에 의해
긴반지름은 Q가 P의 2배여야하고
따라서 긴지름(긴반지름×2)도 2배여야한다.
Q의 긴지름은 (3/2)r0_
P의 긴지름은 (1-2/sqrt(2))r0_ 이므로
2배가 아니다.
따라서 ㄷ(x)
따라서 답은 2번
5 )

행성과 B가 가장 가까울때 만유인력의 크기가 최댓값을 가진다.
이때 행성과 B 사이의 거리를 r이라 놓고 풀었다.

따라서 답은 3번
6 )

ㄱ)
Q에 작용하는 만유인력의 크기는
행성까지의 거리가
A가 C보다 가까우므로
A에서의 만유인력이 더 크다.
따라서 ㄱ(x)
ㄴ)
만유인력 F = ma = GMm/r² 에서
m은 약분된다.
따라서 가속도는 P, Q의 질량과 관계없고
행성과 떨어진 거리와만 관계있다.
근데 B는 떨어진 거리가 같은 지점이므로
가속도의 크기도 같다.
따라서 ㄴ(o)
ㄷ)

1. 저 색칠한 부분의 넓이는
타원의 1/4 이므로
5πR² 이다.

2. 피타고라스 정리에 의해
OB의 길이는 4R이고
따라서 색칠된 삼각형의 넓이는 6R²이다.

따라서 저 색칠된 부분의 넓이는 5πR²-6R²이다.
케플러 제2법칙에 의해
일정 시간에 행성과 인공위성 Q를 잇는 직선이
훑고 지나가는 면적은 같다.
한 주기동안 훑고 지나가는 면적이 20πR² 이므로
이를 이용해 비례식을 세우면

따라서 ㄷ(o)
따라서 답은 4번
7 )


이 식을 이용하여 풀면 된다.

따라서 답은 2번
8 )

ㄱ )
케플러 제2법칙 : 면적 속도 일정 법칙에 의해
같은 시간동안 위성 P와 행성을 연결한 선이 훑고 지나가는 면적이 같아야 하는데
a가 원일점이고 c가 근일점이므로
원일점인 a에서가
근일점인 c에서보다 속력이 느려야한다.
따라서 ㄱ(x)
ㄴ )
심화 1 에서 다뤘던 내용이다.
P는 b점을 지난 후 행성과 가까워지고
Q는 c점을 지난 후 행성과 멀어진다.
따라서 P는 b점에서 만유인력>구심력 이었으며
Q는 c점에서 만유인력<구심력 이었다.
근데 행성과 b지점 사이의 거리
행성과 c지점 사이의 거리는 둘다 d 로 같다.
따라서 각 위성에 작용하는 만유인력의 크기는
각 위성의 질량, 속력만이 관여한다.
근데 질량은 아까 심화 1 에서 다뤘다시피
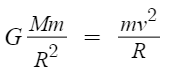
위성의 질량인 m은 계산 과정에서 약분된다.
따라서 결국 만유인력과 구심력의 크기를 비교할때는 위성의 속력만이 관여한다. 라는 결론에 도달한다.
근데 P의 b점에서의 만유인력의 크기 > 구심력의 크기
Q의 c점에서의 만유인력의 크기 < 구심력의 크기
라고 했으므로
P의 b점에서의 속력 < P가 원운동하기 위한 속력
Q의 c점에서의 속력 > Q가 원운동하기 위한 속력
임을 알 수 있다.
근데 아까 만유인력과 구심력의 크기를 비교할때는 위성의 속력만이 관여한다고 했다.
따라서 P가 원운동하기 위한 속력 = Q가 원운동하기 위한 속력 이다.
이를 v 라고 하면
P의 b점에서의 속력 < v < Q의 c점에서의 속력
따라서 ㄴ(o)
ㄷ )

Q의 공전주기가 P의 2sqrt(2) 배 이므로
Q의 공전궤도 긴반지름은 P의 2배이다.
Q의 공전궤도 긴반지름이 3d 이므로
P의 공전궤도 긴반지름은 3d/2 이다.
따라서 P와 행성이 가장 가까울때의 거리는 d/2 이다.
따라서 ㄷ(x)
따라서 답은 1번
'물리II > I. 역학적 상호 작용' 카테고리의 다른 글
| 열에너지 - 열과 일의 전환 (0) | 2021.08.25 |
|---|---|
| 일반 상대성 이론 (1) | 2021.08.24 |
| 물체의 운동 #4 - 단진자 (0) | 2021.08.24 |
| 물체의 운동 #3 - 등속 원운동 (0) | 2021.08.23 |
| 물체의 운동 #1 - 포물선 운동 (0) | 2021.08.22 |



