문제 자체의 난이도는 별로 높지 않은데
계산이 좀 많은편이다.
- 등속 원운동 -
말 그대로 물체가
원 궤도를 그리며 등속력 운동 하는 것이다.
원운동이 무슨 운동이고
어떤 원리로 원운동할 수 있는지에 대한 이해만 있으면
사실상 날로 먹는 단원이다.
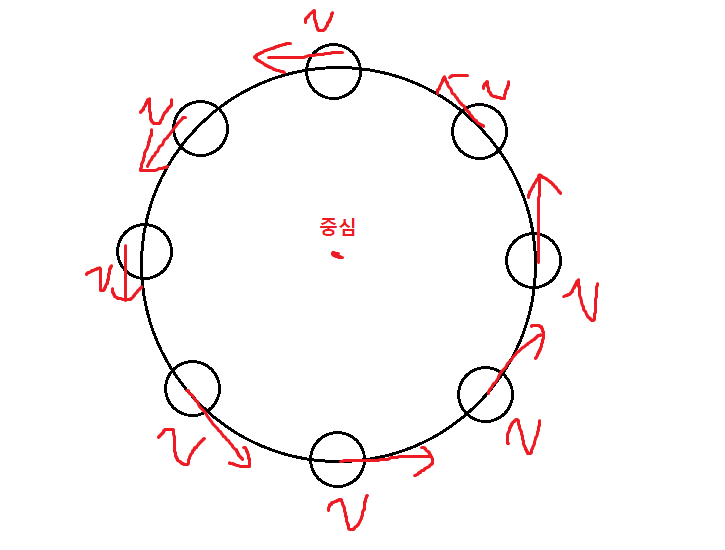
그래서 왜 도는걸까?
돌리니까 도는건 맞는데
그 돌린다는게 정확히 뭐냐는것이다.
그림상 물체는 계속 중심에서 멀어지는 방향의 속도를 갖고있는데
어떻게 중심을 끼고 도는걸까?
일단 저 운동은 등속력 운동이지만
속도의 방향은 계속 바뀌기때문에
등속도 운동은 아니다.
그럼 속도가 변했다는건 가속도가 있었다는거고
가속도가 있었다는건 힘이 있었다는거다.
따라서 저 물체에 계속 힘을 가해서
원 궤도를 따라 돌도록 한것이다.
이때 물체가 원운동하도록 하는 힘을
'구심력' 이라 한다.
그럼 이건 등가속도 운동인가?
그것도 아니다.
가속도도 방향을 갖는 벡터인데
가속도의 방향도 계속 바뀌기 때문이다.
우리는 계속 등가속도운동만 해왔기 때문에
우리가 지금까지 알고있는것만으로
이 운동을 기술하기는 무리다.
즉 원운동을 만드는 구심력을 기술하기 위해
새로운 개념이 들어와야한다.
- 각속도와 선속도 -
각속도 : 각이 돌아가는 속도
선속도 : 우리가 여태 쓰던 그 속도
저 그림에서 v는 다 선속도이다.
- 각속도의 정의 -
선속도와 마찬가지로
일정 시간 간격 동안의 각도 변화량이 각속도이다.
ω 라고 쓴다.
더블유가 아니라 오메가 이다.
이때 각도의 단위는 라디안(rad)이다.
수학할때 삼각함수에 들어가는 변수와 단위가 같다고 보면 된다.
sin(π) = 0 이런식 이라는거다.
즉 앞으로의 원운동에서 각도는 π로 나타내어진다고 보면 된다.
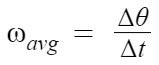
평균변화율이므로 avg를 붙였다.
근데 우린 어떤 순간의 각의 순간변화율을 알고싶다.
그럼 Δt→0으로 극한때리면된다.
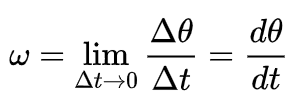
따라서 ω = dθ/dt 이다.
우리는 등속 원운동을 다루므로
평균 각속도가 곧 각속도다.
즉 각속도의 크기는 항상 일정하다.
우리가 이전에 했던것도
등가속도운동이니까 가속도를 일정한 a라 놓고
물체의 운동을 기술할수 있었던것이다.

이젠 선속도를 구해보자.
- 각속도와 선속도의 관계 -
선속도는
이동거리를 s라 하면
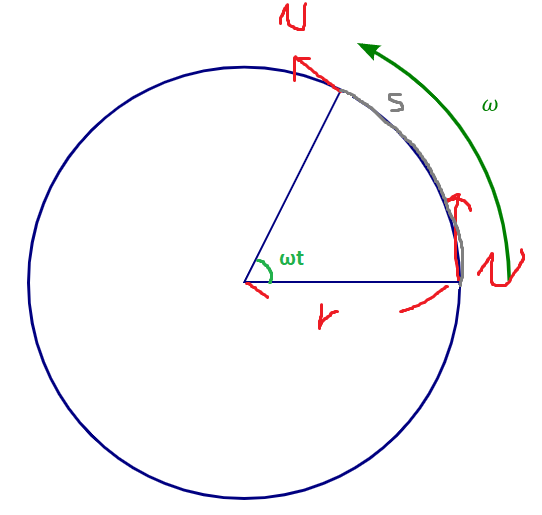
물체는 원운동하므로
Δt초간 물체의 이동거리는
저 부채꼴 모양의 호의 길이이고
각도 x 원의 반지름 = 호의 길이 이므로
각도 = ω × Δt
원의 반지름 = r
따라서 s = rωΔt
따라서 이때의 선속도는
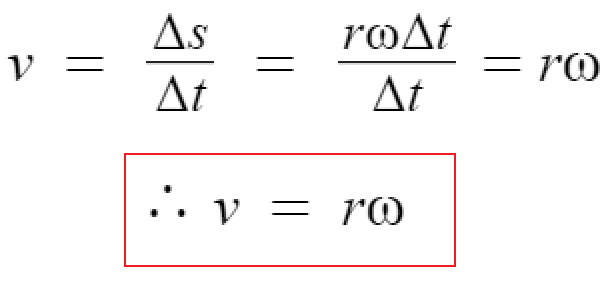
즉 선속도 = 각속도 × 원운동 궤도의 반지름 이다.
앞으로 등장하는 r도 모두 원운동 궤도의 반지름이라는걸 기억하자.
- 원운동의 주기 -
물체가 원 궤도로 한 바퀴 도는 데 걸리는 시간이다.
T라고 쓴다.
한바퀴 돈다는건
2π 돌았다는거다.
따라서 T시간동안 2π 돌았다는거를
아까 각속도 식에 넣으면
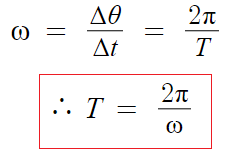
- 원운동의 진동수(frequency) -
한바퀴 도는데 걸리는 시간이 주기면
1초동안 몇바퀴 도느냐를 나타내는게 진동수다.
단위는 Hz 또는 1/s 다.
즉 진동수는 주기의 역수이다.
따라서 f = 1/T 이고
아까 주기 식을 여기다 대입하면
각속도의 또 다른 식이 나온다.

- 요약 -
등속 원운동이란, 물체가 원 궤도로
같은 속력으로 운동하는것이다.
이때 물체가 원 궤도로 등속력 운동 하도록 하는 힘을
'구심력' 이라 한다.



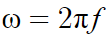
- 구심 가속도 -
우선 구심력의 크기는
당연히 F=ma이고
구심력을 알기 위해 구심가속도 부터 알아야한다.

이 그림으로 돌아가보자.
가속도는
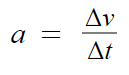
따라서 저 그림에서 다 떼버리고
각도에 따른 속도의 변화량만 보자.
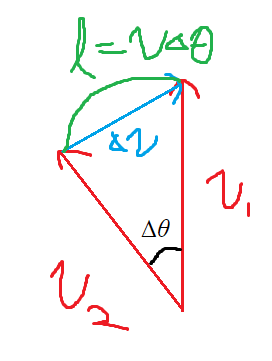
이건데 어떤 순간의 가속도를 알기 위해
Δt→0으로 극한때리면

이렇게 될거다.
근데 Δθ = ωΔt 이다.
따라서 Δt→0 이면
Δθ 도 0에 수렴할것이고
결국 다음과 같이 될것이다.
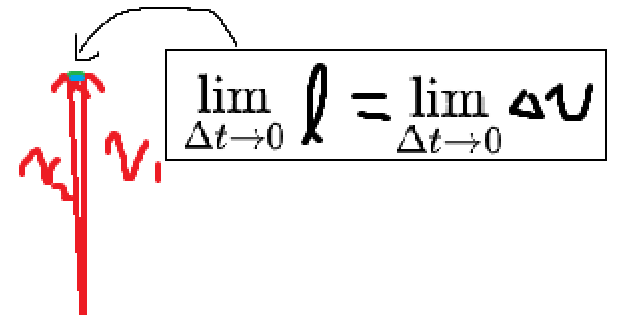
즉 각의 크기가 아주 작으면
v1, v2, ℓ로 이루어진 부채꼴에서 호 ℓ 의 길이나
v1, v2, Δv로 이루어진 삼각형의 변 Δv 의 길이나
같다고 볼 수 있다는것이다.
따라서 이를 이용하여 a를 정리하면

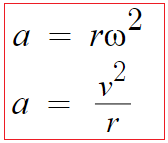
저게 구심가속도다.
따라서 구심력은 F=ma 이므로

식이 엄청나게 많다.
공식의 암기와 함께
공식에 들어가는 물리량들의 의미를 파악하고 있으면
문제는 쉽게 풀 수 있다.
- 구심력의 방향 -
아까 Δt→0 으로 극한때렸는데
같은 방식으로 해보자.
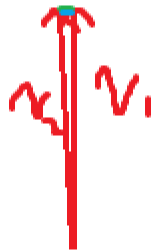
각이 무한히 작다.
그러면 Δv는 v1_과 수직 방향일 것이다.
Δv의 방향이 곧 가속도의 방향이고
가속도의 방향이 속도와 수직 방향이므로
구심력은 물체의 속도와 수직한 방향이다.
라는 결론이 나온다.
근데 물체의 속도의 방향은
원의 접선 방향이다.
따라서 구심력의 방향은
원의 접선과 수직한 방향이고
원의 중심을 향하게 된다.
구심가속도는 한자로 求心加速度 이다.
여기서의 求는 '공 구'가 아니라
구하다, 빌다, 책망하다, 탐내다, 다잡다 라는 뜻을 가진
'구할 구' 이다.
따라서 중심(心)으로 가기를 원한다(求) / 구심가속도.
이해가 잘 안될텐데
원래 한번에 이해하기 어려운 곳이다.
이해를 돕기 위해 간단하게 몇가지 묻겠다.

ㅇ중력장에서 질량 m인 물체가 실에 매달려서
수평면 상에서 각속도 ω로 빨간 화살표 방향으로
등속 원운동 하고있다.
실과 축이 이루는 각은 θ이다.
공기마찰 및 지구 자전 효과는 무시한다.
1. 등속도 운동인가?
2. 등가속도 운동인가?
3. 가속도의 크기가 일정한 운동인가?
4. 이때 물체에 작용하는 힘들을 표시해라.
5. 이때 물체에 작용하는 힘들의 합력의 방향은?
6. 이때 물체의 운동 방향은?
7. 실의 길이가 L이라면, 구심 가속도의 크기는?
8. 도는 동안 물체의 역학적 에너지는 보존되는가?
1 )
속도의 방향이 계속 변하므로 등속도 운동이 아니다.
단 속도의 크기는 일정하다.
2 )
가속도의 방향이 계속 변하므로 등가속도 운동이 아니다.
단 가속도의 크기는 일정하다.
3 )
첫째, 등속력 원운동이기 때문에
가속도의 크기는 일정하다.
둘째, 구심가속도는
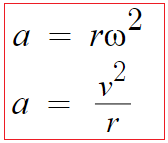
이 식에 따라서도 일정하다.
4 )

물체에 작용하는 힘은 장력과 중력밖에 없다.
5 )
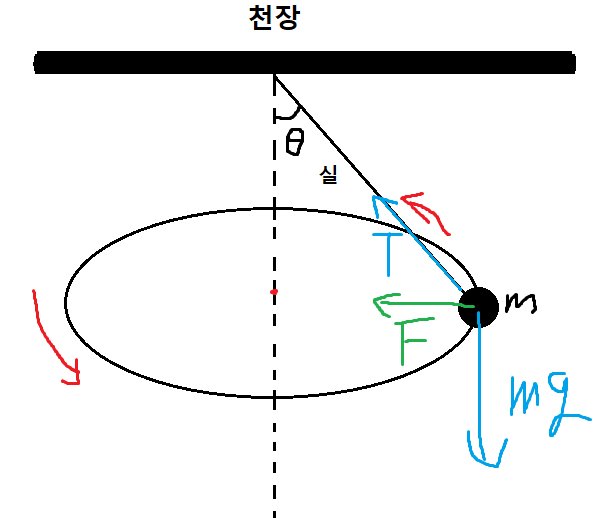
합력의 방향이 원의 중심을 향하기 때문에
이게 구심력의 역할을 해서
등속 원운동 할 수 있는 것이다.
6 )
물체의 운동 방향은
그 점에서의 원의 접선 방향이다.
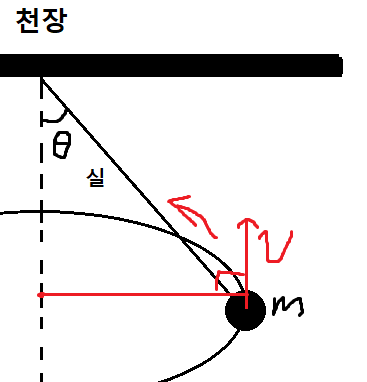
3차원을 2차원으로 표현하려니 한계가 있는데
천장방향 아니다.
원의 접선 방향이다.
7 )

8 )
우선 수평면 상에서 돌고있으므로
위치에너지는 변하지 않는다.
근데 등속 원운동이므로
운동에너지도 변하지 않는다.
따라서 역학적에너지는 보존된다.
여기서 질문이 들어올 수 있다.
많이들 갖고있는 오개념이라 주의가 필요한데
실이 당기는 힘은 엄연히 '비보존력' 인데
어떻게 역학적에너지가 보존되는건가?
일-에너지 정리를 떠올려보자.
실이 당기는 힘과
물체의 운동 방향은 수직이다.
힘의 방향과 운동 방향이 수직이면
한 일은 0이 된다.
즉 운동방향과 수직인 힘은
역학적에너지에 아무 영향을 끼치지 못한다.
- 식 요약 -
식이 많아서 하나로 모아보겠다.
1. 각속도

2. 선속도

3. 주기

4. 각속도를 진동수로 나타내면
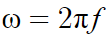
5. 구심가속도

6. 구심력

식이 많기 때문에
문제를 보고 알아서 식을 잘 써서 풀어야한다.
예를 들어 A와 B의 각속도가 같다면
A와 B 사이의 물리량들을 비교하라는 문제가 나왔을때
각속도가 들어간 식을 써주면
각속도가 같으니 나머지만 비교하면 되는것이다.
하나만 더 풀어보자.
A와 B가 둘다 원운동중이고
둘의 질량과 원운동 궤도 반지름은 같다.
A와 B에 작용하는 구심력이 4 : 1 이면
주기는 A가 B의 몇배인가?
풀이 )
구심력이 4 : 1이므로
A의 각속도는 B의 2배이고
각속도가 2배이므로 주기는 1/2배이다.
- 예제 -
1 )

ㄱ)
둘의 원운동 궤도 반지름이 같고
선속도도 같으니
주기도 같다.
따라서 ㄱ(o)
수식으로 풀자면
T = 2π/ω
v = Rω
v 같고 R 같으니 ω도 같고
따라서 주기도 같다.
ㄴ)
구심 가속도는
a = Rω² 또는
a = v²/R 인데
R과 v가 주어졌으니 아래껄로 푸는게 더 빠르다.
R 같고 v 같으니 a도 같다.
따라서 ㄴ(o)
ㄷ)
구심력의 크기는 질량 × 구심가속도 인데
ㄴ 에서 구심가속도가 같다는걸 알았으므로
질량이 더 큰 B가 더 구심력이 크다.
따라서 ㄷ(x)
수식으로 풀기)
Fa = mv²/R
Fb = 2mv²/R
따라서 답은 4번
2 )

ㄱ)
A와 B가 직선 막대에 고정되어있다.
따라서 둘은 같이 돌것이다.
즉 둘의 각속도가 같다.
따라서 ㄱ(x)
ㄴ)
A와 B는 각속도가 같은데
B의 궤도 반지름이 더 크므로
B의 속력이 더 빠르다.
수식으로 풀자면 v = rω인데
ω 같고 r은 B가 더 크니 v도 B가 더 크다.
따라서 ㄴ(o)
ㄷ)
구심 가속도는
a = rω² 인데
각속도는 A와 B가 같고
궤도 반지름은 B가 더 크므로
구심가속도도 B가 더 크다.
따라서 ㄷ(o)
따라서 답은 4번
3 )

ㄱ)
실이 고무마개를 당기는 힘의 크기는
추의 무게 이다.
추의 질량이 2배가 됐으므로
추의 무게도 2배가 됐고
따라서 당기는 힘의 크기도 2배가 된다.
따라서 ㄱ(x)
ㄴ)
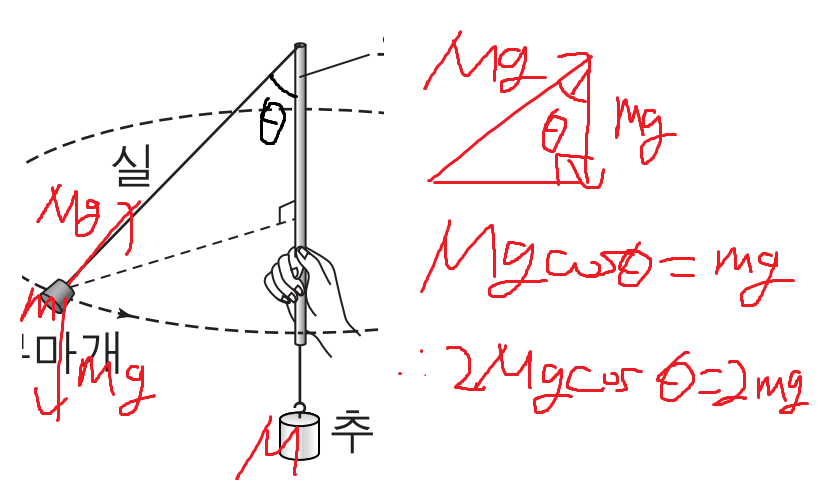
고무마개에 작용하는 힘은
실이 당기는 힘(Mg)과
고무마개에 작용하는 중력(mg)
이거 두갠데
Mgcosθ = mg 를 만족하기때문에
이 둘의 합력이 구심력의 역할을 할 수 있는것이다.
추와 고무마개의 질량을 둘다 2배로 하면
실이 당기는 힘 2Mg
중력 2mg
이것도 2Mgcosθ = 2mg 를 만족하므로
실과 유리관이 이루는 각은 변하지 않는다.
따라서 ㄴ(o)
ㄷ)
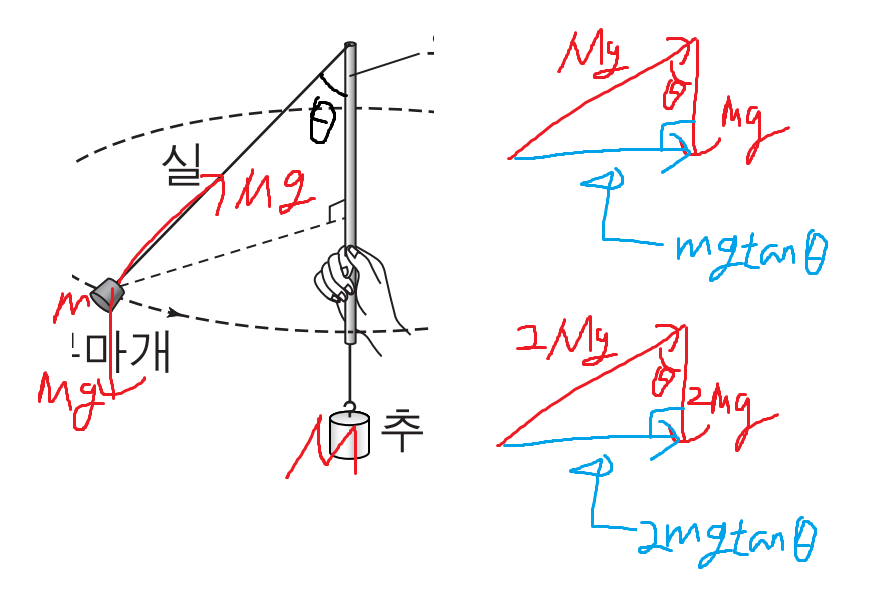
따라서 구심력의 크기는 2배가 된다.
따라서 ㄷ(x)
따라서 답은 2번
4 )

ㄱ)
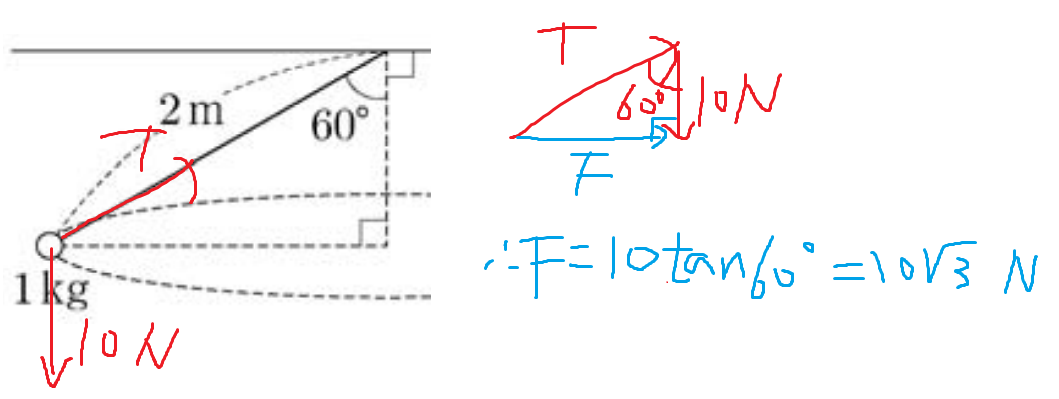
따라서 ㄱ(o)
ㄴ)
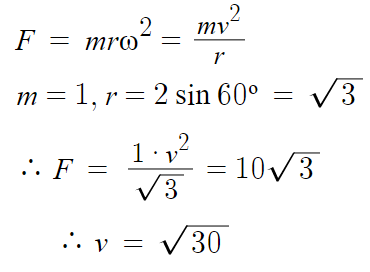
따라서 ㄴ(o)
ㄷ)
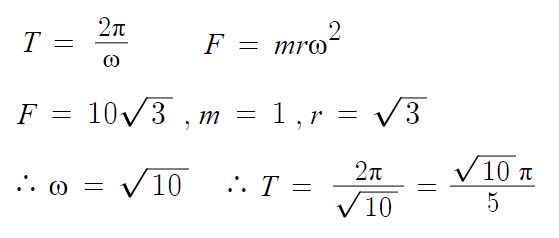
따라서 ㄷ(x)
따라서 답은 3번
5 )

ㄱ)
그래프상 한 주기가 4π인걸 알 수 있다.
따라서 4π = 2π/ω이고
따라서 각속도의 크기는 0.5rad/s 이다.
따라서 ㄱ(x)
ㄴ)
x의 최댓값이 2m인걸 보니
원운동 궤도 반지름이 2m인 원운동이라는걸 알 수 있다.
v = rω = 2 × 0.5 = 1
따라서 ㄴ(o)
ㄷ)
가속도의 크기 = 구심가속도의 크기
= rω² 또는 v²/r
r=2, ω=0.5, v=1이니까 아무 식에나 대입하면
가속도의 크기는 1/2(m/s²) 이다.
따라서 ㄷ(x)
따라서 답은 2번
6 )

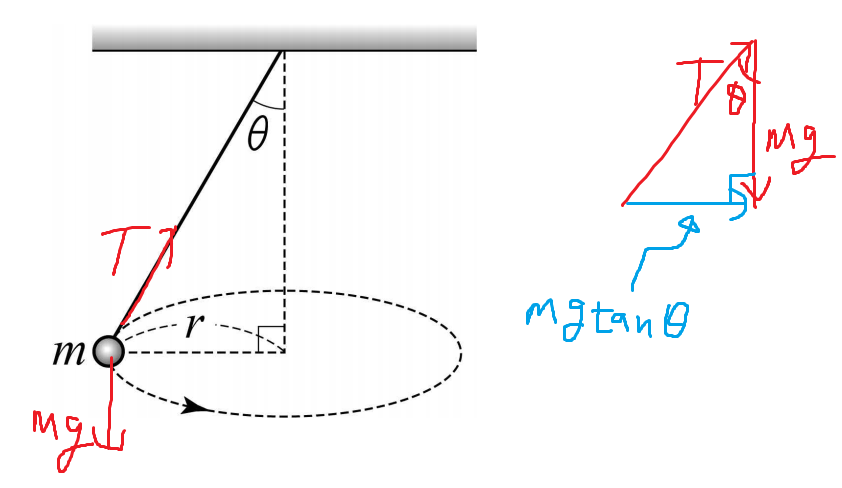
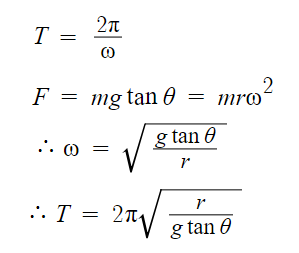
따라서 답은 5번
7 )

ㄱ)
물체가 B를 지날때 물체의 가속도 방향을 알기 위해
물체에 작용하는 힘을 표시해보자.
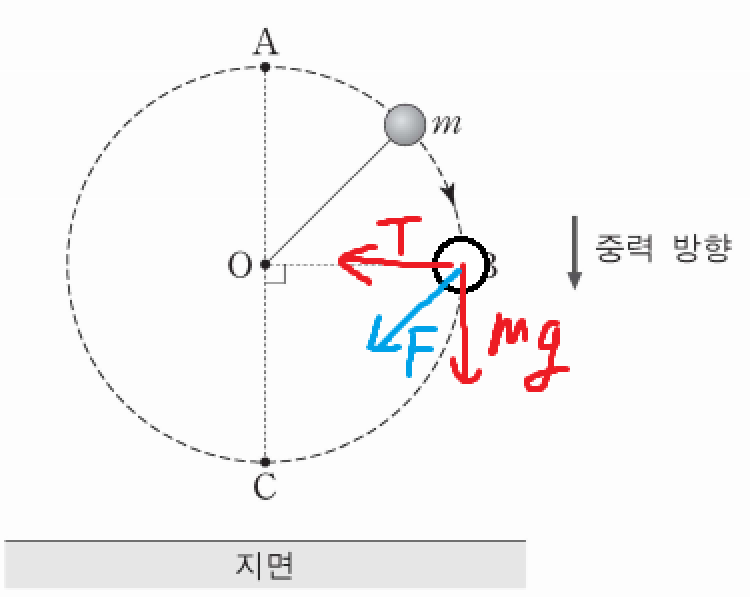
합력의 방향이 중력 방향이 아님을 알 수 있다.
게다가 원운동인데 O 방향도 아니다.
이는 이 운동이 등속 원운동이 아님을 알려주고 있는 부분이다.
따라서 ㄱ(x)
ㄴ)
물체의 역학적 에너지는 보존된다.
물체에 작용하는 비보존력은 장력 뿐인데
장력과 물체의 이동방향이 수직이라서
장력이 하는 일이 0이 되기 때문이다.
따라서 저 원운동의 궤도 반지름을 R이라 하고
역학적 에너지 보존 식을 쓰면
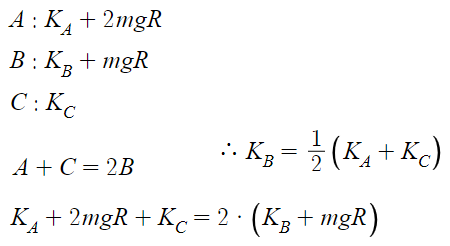
따라서 ㄴ(o)
사실 역학적 에너지가 보존된다는것만 알면
굳이 저렇게 식을 쓰지 않아도 눈치챌 수 있는데
등속이 아닌 원운동은 처음 볼테고
난이도 있는 문제기도 하니까 친절하게 다 써줬다.
ㄷ)
ㄴ을 풀면서
C지점의 운동에너지가 더 크니까
C지점의 속력이
A지점의 속력보다 빠르다는걸 알았다.
따라서 C지점에서의 구심력이
A지점에서의 구심력보다 크고
C지점에서 작용하는 힘은
위쪽방향 장력
아래쪽방향 중력
따라서 장력만으로 구심력을 만들어야한다.
반면 A는 장력+중력으로 구심력을 만들어야하는데
구심력의 크기도 A가 더 작다.
따라서 실의 장력의 크기는 C를 지날때가
A를 지날때보다 크다.
따라서 ㄷ(o)
수식으로도 풀 수 있다.
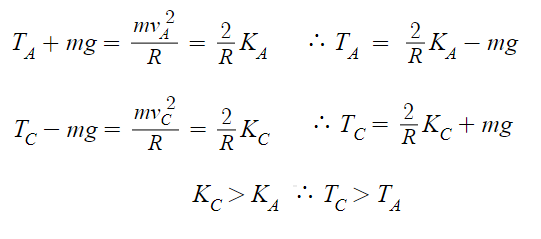
따라서 답은 6번
'물리II > I. 역학적 상호 작용' 카테고리의 다른 글
| 물체의 운동 #5 - 케플러 법칙과 만유인력 (0) | 2021.08.24 |
|---|---|
| 물체의 운동 #4 - 단진자 (0) | 2021.08.24 |
| 물체의 운동 #1 - 포물선 운동 (0) | 2021.08.22 |
| 힘과 운동 #2 - 물체의 평형 (0) | 2021.08.21 |
| 힘과 운동 #1 - 힘의 합성과 분해 (0) | 2021.08.20 |



