
- 개요 -
이번에도 등차수열과 마찬가지로
특별한 규칙이 있는 수열을 다룰 것이다.
- 등비수열 -
등비수열 : 연속하는 두 항의 비가 모두 일정한 수열
가령 2, 4, 8, 16, 32, ... 와 같은 수열이 있다면
연속하는 두 항의 비는
제1항과 제2항의 비율 = 1 : 2
제2항과 제3항의 비율 = 1 : 2
제3항과 제4항의 비율 = 1 : 2
따라서 이건 등비수열이다.
이때 두 항의 비는
수열의 모든 연속하는 두 항들의 공통적인 비 이므로
공비 라고 한다.
즉 등비수열에서 연속하는 두 항의 비가 공비이다.
아까 예로 들었던 2, 4, 8, 16, 32, ... 이 수열은
공비가 2인 등비수열이다.
공비는 영어로 common ratio 이고, 기호 r로 쓴다.
- 등비수열의 일반항 -
2, 4, 8, 16, 32, ... 이 수열의 일반항은 무엇일까?
우선 제1항은 2이고
공비가 2이므로
제2항은 2×2 이다.
제3항은 2×2×2 이다.
제4항은 2×2×2×2 이다.
즉 제n항의 값은 2×2^(n-1) 이다.
여기서 2는 제1항 이고
2는 공비이고
n-1은 공비가 n-1번 곱해진다는 의미이다.
따라서 이 수열의 일반항은
2ⁿ 이다.
따라서 일반화 시키면
등비수열의 일반항은 다음과 같다.

- 등비중항 -
세 수 a, b, c 가 이 순서대로 등비수열을 이룰 때
b를 a와 c의 등비중항 이라고 한다.
a, b, c 가 등비수열이므로
b/a = c/b 이고
정리하면 b² = ac 이다.
양변에 제곱근을 취하면
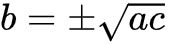
이는 a와 c의 기하평균과 같다.
- 등비수열의 합 -
조금 복잡해보이는 공식이 있긴 한데
매우 간단한 논리니까
공식을 외우지 말고 스스로 유도해보자.
등비수열의 첫째항부터 제 n항까지의 합을

이렇게 쓴다.


- 등차수열과 등비수열의 관계 -
하나는 덧셈이고 하나는 곱셈이라
아무 관련 없을거같지만 사실 특별한 관계를 가지고 있다.
등비수열의 각 항에 로그를 취해보자.

이는 첫 항이 log2 이고 공차가 log2인 등차수열이다.
따라서 등비수열의 각 항에 로그를 취하면 등차수열이 된다.
이번엔 반대로 어떤 수에 등차수열의 각 항을 거듭제곱으로 취해보자.
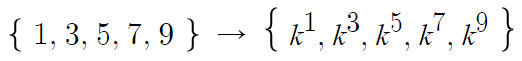
이는 첫 항이 k 이고 공비가 k² 인 등비수열이다.
따라서 등차수열의 각 항을 어떤 수의 거듭제곱으로 취하면 등비수열이 된다.
예제와 함께 마무리
- 예제 -
1 )

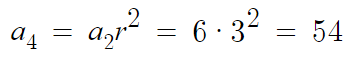
따라서 답은 54
2 )

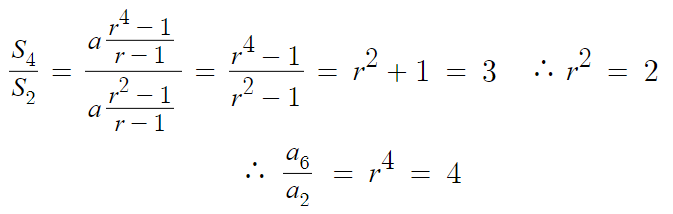
따라서 답은 4
3 )


따라서 답은 1번



