'귀납' 이라는 단어가 생소해서
어려울거같지만 쉬운곳이다.
- 귀납법 -
귀납 추론 이라고도 한다.
경험적으로 알아낼 수 있는 특수한 사실이 있을것이다.
그리고 이 경험이 반복되면
이 특수한 사실들 사이에서 공통성을 추론할 수 있게 되고
그것을 일반화하여 일반적인 결론을 내는 방법이 귀납법이다.
필연적인 근거로부터 시작하는 연역법과는 추론의 방향이 반대이다.
예를 들자면
a, b, c, d, e, ... 이런 수열이 있다고 해보자.
b-a 값을 X라 했더니
c-b도 X이고
d-c도 X이고
e-d도 X이다.
직접 앞의 항과 뒤의 항의 차이를 구해보는 경험을 통해
둘의 차이가 X로 같다는 공통성을 찾아냈다.
따라서 연속하는 두 항의 차이가 일정하니까
이건 등차수열이겠구나. 라고 추론하는게 귀납법이다.
물론 언젠가 둘의 차이가 X가 아닌 경우가 등장할 수도 있으니
필연성은 부족하다는 한계가 있다.
- 수학적 귀납법 -
자연수 n에 대한 명제 p(n)이 모든 자연수 n에 대하여 성립한다는 것을
귀납법을 통해 증명하려면
다음 두 가지를 보이면 된다.
1. n=1 일 때, 명제 p(n)이 성립한다.
2. n=k 일 때, 명제 p(n)이 성립한다고 가정하면
n=k+1 일때도 명제 p(n)이 성립한다.
조금 쉽게 설명하자면
모든 자연수 n에 대하여 p(n)이 성립하는걸 보이려면
우선 p(1)이 성립한다는걸 보여준 뒤
p(k)가 성립한다고 가정했을때 p(k+1)도 성립한다면
p(1)이 성립하면 p(2)도 성립한다는거다.
k=1 이라 하면 p(1)이 성립하므로 p(2)도 성립하고
k=2 이라 하면 p(2)가 성립하므로 p(3)도 성립하고
이를 반복하면 모든 자연수 n에 대하여 p(n)이 성립한다는 것이 증명 완료된다.
- 수열의 귀납적 정의 -
처음 몇 개의 항과
이웃하는 여러 항 사이의 관계식으로 수열을 정의하는 것을
수열의 귀납적 정의라고 한다.
일반적으로, 수열 {a_n} 을 다음과 같이 귀납적으로 정의할 수 있다.
1. 첫째항 a_1 의 값
2. 두 항 a_n , a_n+1 사이의 관계식

이런식으로 정의하면
a_2 의 값을 구하라 하면
a_1의 값을 알고 있으므로
n=1이라 했을 때 아래의 식에 대입하면
a_2 = 7 임을 알 수 있다.
아까 위에 수학적 귀납법에 적어놓은 걸 그대로 가져오겠다.
1. n=1 일 때, 명제 p(n)이 성립한다.
2. n=k 일 때, 명제 p(n)이 성립한다고 가정하면
n=k+1 일때도 명제 p(n)이 성립한다.
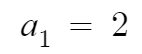
1. n=1일때 이게 성립한다.

2. n=k일때 이게 성립한다고 가정하고
n=k+1 일때도 이게 성립한다면
모든 자연수에 대해 성립하게 되고
이 수열을 귀납적으로 정의할 수 있게 되는것이다.
예제와 함께 마무리할건데
문제는 쉽게 나온다.
아까 귀납법을 설명할때
여러 경험들 사이에서의 공통성을 찾아내는 추론법이라 했다.
즉 귀납법 문제를 풀때는
직접 수를 대입해보자.
대입하는 경험을 여러번 시행하여
공통성을 찾은다음 일반화 하는것이다.
예를 들어 다음 수열의 일반항을 구해보자.
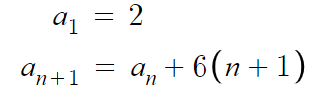
일반항을 구하라는건 a_n = (n에 대한 식) 으로 나타내라는 것이다.
등차수열이라 하기도 애매하고 뭔가 잘 모르겠다.
그래서 n에 값을 하나씩 대입해보고 규칙성을 찾아보겠다.
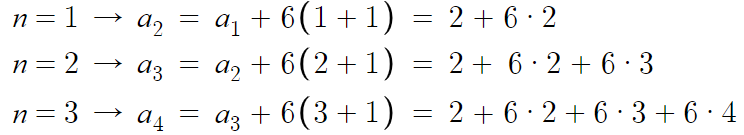
3개쯤 대입하니까 규칙이 보인다.
2에다가 6k 의 값을 k=1부터 k=n까지 전부 더한 다음 6을 뺀게 a_n 의 값이다.

따라서 정리하면 일반항은 다음과 같다.
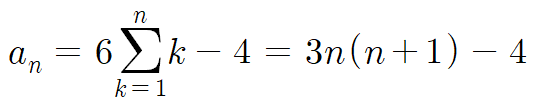
요약하자면
수학적 귀납법 문제는
하나씩 대입하면서 규칙성을 찾는 방향으로 푼다.
- 예제 -
1 )

수학적 귀납법 문제는 어떻게 푼다?
하나씩 대입해서 푼다.

따라서 답은 33
2 )


다소 난이도있는 문제이다.
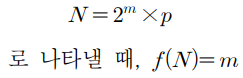
인데
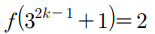
이므로

여기서 m=2 이다.
따라서 (가)는 2^2 = 4 이다.
따라서 a=4
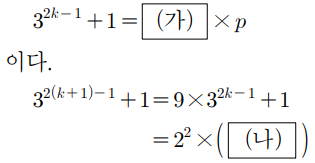
n=k 일때 성립한다 가정하면
n=k+1 에서도 성립하는지를 보는 과정임을 알 수 있다.

따라서 (나)는 9p-2 이다.
따라서 a + g(7) = 4 + (9×7-2) = 65
따라서 답은 65
수학1 끝



