이번 주제는
물리의 물 자도 모르는 사람들도 누구나 아는 사람인
아인슈타인이란 과학자가 발표한 논문 5가지중 하나인
'특수 상대성 이론' 이다.
발표될 당시 엄청난 충격에 휩싸였다고 한다.
너무 어려운 이론이라
이것도 열역학하듯이 일단 암기해놓고 문제풀이로 감을 잡는게 좋다.
조금만 삐끗하면 바로 오개념이 잡혀서
자기 논리에 자기가 빠져서 헤어나오지 못하는 일이 많은 곳이다.
- 관성 좌표계 -
관성 좌표계 : 고전역학에서 뉴턴의 운동법칙 중 제1법칙이 성립하는 좌표계
뉴턴 제1 운동법칙이 뭐였냐면
관성법칙이라고도 하는데
물체에 작용하는 알짜힘(합력)이 0이면
정지해 있던 물체는 계속 정지해있고
운동하던 물체는 속도 변화 없는 등속도운동을 한다.
쉽게 말해서 뉴턴의 관성법칙이 성립하는 공간이라 보면 된다.
예를 들어
우리가 버스를 타고 서서 정지해있었는데
버스가 급출발(가속)을 하면
우리는 뒤로 넘어지게된다.
알짜힘이 0인데 가속도운동을 하게 된것이다.
따라서 가속하는 버스는 관성의 법칙에 위배되므로
가속하는 버스는 관성 좌표계가 아니다.
만약 버스가 일정한 속도로 움직이면(가속도가 0이면)
우리는 딱히 노력 없이도 계속 가만히 서있을수 있다.
알짜힘 0에 속도 변화량도 0이므로
일정한 속도로 움직이는 버스는 관성 좌표계이다.
잘 와닿지 않을텐데
문제 풀다보면 아 당연한말이구나 하고 이해할테니 이쯤 하고 넘어가겠다.
- 특수 상대성 이론 -
이게 왜 큰 충격이었냐면
여태 쌓아온 역학의 체계를 한번에 흔들었음은 물론이고
기존 역학으로는 설명이 안되던 현상들이
이 이론을 적용하자 딱 들어맞았던 것이다.
우리가 여태 등가속도운동에서 이동거리는 v0t + 어쩌고
운동에너지는 1/2 x mv² 하는식으로
질량, 시간 등으로 물체의 운동을 기술했었다.
근데 이 이론에 따르면
질량, 시간, 공간 모두 절대적이지 않고 상대적이다.
절대적이라는건
누군가 물체가 운동한 시간이 3초 라고 관측했으면
다른 누군가가 어디서 어떻게 관측해도
운동시간이 3초 라고 관측되어야 한다는것이다.
근데 이 이론에 따르면
시간은 상대적이므로 다른 누군가가 관측했을때
이 물체의 운동시간은 3초가 아닐수도 있다.
3.0001초라 관측할수도 있고 4초라 관측할수도 있다.
즉 관찰자가 누구냐에 따라서 운동이 다르게 기술될수도 있다는것이다.
그러면 절대적인 기준이 없는데
물체의 운동을 대체 어떻게 기술해야 할까?
- 특수 상대성 이론의 가정 -
1. 상대성의 원리
상대성의 원리 : 모든 관성 좌표계에서 물리 법칙은 동일하게 성립한다.
쉽게 말해서
등속도로 달리는 버스 안에서 공을 위로 던지면
버스에 10명이 타고있든 100명이 타고있든
버스에 타고있는 모든 사람들에게는
공이 그냥 위로 올라갔다 내려오는 것처럼 보일것이다.
근데 버스 정류장에서 버스를 기다리면서 가만히 서있는 사람들이 보기엔
공이 포물선 운동한것처럼 보일것이다.
즉 '등속도로 달리는 버스 안' 이라는 관성 좌표계에서는
공이 위로 올라갔다가 내려오는 운동으로 기술될것이고
'버스정류장' 이라는 관성 좌표계에서는
공이 포물선 운동하는 운동으로 기술될것이다.
2. 광속 불변의 법칙 ( 매우 중요 )
광속 불변의 법칙 : 모든 관성 좌표계에서 보았을 때,
진공 중에서 진행하는 빛의 속력은
관찰자나 광원의 속도에 상관없이 항상 일정하다.
쉽게 말해서
진공에서 빛의 속력은 누가 어디서 어떻게 관찰하든 항상 같다.
아까 시간도 상대적이고 공간도 상대적이면
대체 뭘로 운동을 기술해야 할까 했는데
운동을 기술할 절대적인 기준을 '광속'으로 둔것이다.
기존 뉴턴역학에 따르면
빛의 속도는
내 운동속도에 따른 상대속도가 있기 때문에
빛의 속도는 원래 속도보다 빠르거나 느리게 측정되어야한다.
근데 빛의 속도가 항상 일정하다는 것이다.
빛의 속력은 보통 c라 쓰는데
내가 빛을 쏜다음 0.5c라는 속도로 달리면
빛의 속력이 1.5c도 아니고 0.5c도 아닌 c로 관측된다는것이다.
그 상황을 가만히 서서 지켜보던 사람에게도 c로 관측된다.
솔직히 너무 어려운 이론이고
나도 이해가 안되는 부분이라 적당히 외워놓고있다.
요약하자면
뉴턴 역학 :
물체의 운동을 기술하는 절대적인 기준은 시간, 공간이고
빛의 속도는 관측자의 속도에 따라 다르게 관측될것이다.
아인슈타인 역학 :
시간, 공간은 상대적이므로 물체의 운동을 기술할 절대적인 기준이 될 수 없고
빛의 속력은 관측자에 상관없이 일정하므로
이를 절대적인 기준으로 운동을 기술해야한다.
- 동시성의 상대성 -
관찰자 A의 눈에 동시에 일어난 것으로 관찰된 어떤 두 사건은
A에 대해 상대운동을 하는 외부관찰자 B의 눈에는 동시에 일어난 것으로 보이지 않는다.
1. 같은 관성 좌표계 안에서의 동시성

철수는 A와 B의 중점에 서있다고 해보자.
그러면 철수 입장에서는
A와 B에서 방출된 두 빛이 철수에게 동시에 도달한다.
영희 입장에서는
A에서 방출된 빛이 먼저 도착하고 B에서 방출된 빛이 나중에 도달한다.
그러나 영희는 본인이 A에 더 가까이 있다는것을 알고 있으므로
두 빛이 동시에 발생했다고 생각하게 된다.
즉 같은 관성계 안에서의 두 사건은 관측자 모두 동시에 일어난 사건으로 인식하게 된다.
2. 서로 다른 관성 좌표계 안에서의 동시성

영희는 우주선을 타고 있고
우주선은 철수가 보기에 A→B 방향으로 v의 속력으로 움직인다.
영희, 철수 모두 A, B의 가운데 지점에 있는 순간이라 해보자.
이 순간 A, B에서 동시에 빛을 방출하면
철수 입장에서는
두 빛이 동시에 도달하므로
두 빛이 동시에 발생한 빛이라 인식한다.
영희 입장에서는
파란색 빛이 발생한 지점을 향해 움직이고 있으므로
파란색 빛이 빨간색 빛보다 먼저 도달한다.
따라서 영희는
파란색 빛이 빨간색 빛보다 먼저 발생한 빛이라고 인식하게 된다.
따라서 서로 다른 관성 좌표계에서는
같은 사건이라도
관측자에 따라 동시에 인식될수도, 아닐수도 있다.
- 시간 팽창 -
시간 지연이라고도 한다.
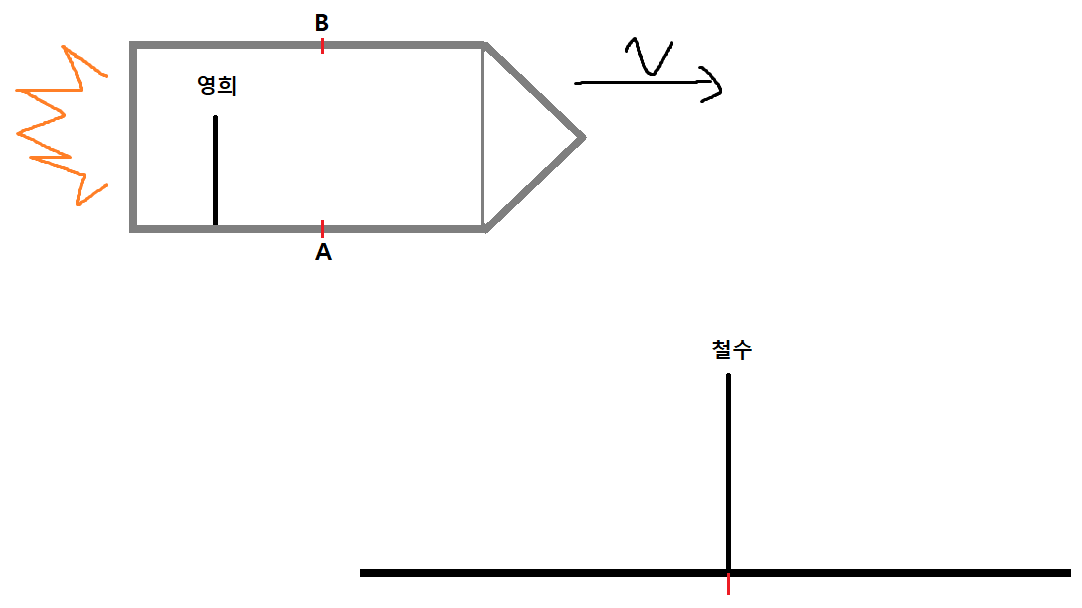
아까와 같은 상황에서
이번엔 우주선 안에서 A에서 거울 B를 향해 빛을 쐈다고 해보자.
빛은 거울 B에서 반사되어 A로 그대로 돌아왔다.
그럼 영희 입장에서 이 빛의 운동은 이렇게 보일것이다.

B에서 반사돼서 A로 그대로 돌아온다.
왜냐면 영희와 우주선은 같은 관성좌표계에 있으니까
- 고유시간 -
사건이 일어나는 곳과 같은 운동 상태인 관찰자가 측정한 시간이 고유시간이다.
예를 들자면
여기서 영희가 측정한 시간이 고유시간이다.
참고로 고유시간이 존재하지 않을수도 있는데
두 사건이 같은 장소에서 발생한 것처럼 보이는 관성좌표계가 존재하지 않는다면
그 경우에는 고유시간은 존재하지 않는다.
예를 들어서 A에서 B를 향해 빛을 편도로 발사했을경우
이때는 빛을 방출한다는 A 사건과
빛이 도달한다는 B 사건이
발생한 장소가 다르다.
그런데 철수 입장에서 이 빛의 운동은 이렇게 보일것이다.

이러면
철수가 봤을때가
영희가 봤을때보다
빛의 이동 거리가 길고
빛의 속력은 항상 일정하니
B에 도달하는 시간은
철수가 봤을 때가
영희가 봤을 때보다 더 길다.
즉 철수 입장에서 영희의 시간은 느리게 간다.
철수의 관성계에서
영희의 관성계에서의 사건을 관측했더니
'시간이 팽창'한것이다.
그나마 쉽게 요약하자면
이 우주선이라는 관성계에서
빛을 A에서 방출하는 사건
A로 빛이 다시 도달하는 사건
이 두 개의 사건이
영희의 입장에서 보면 같은 장소에서 발생했고
따라서 두 사건의 시간차를 재면 그게 고유시간이다.
즉 두 개의 사건이 어떤 관성좌표계에서 같은 장소에서 발생하였을 때,
그 관성좌표계에서의 두 사건의 시간차가 고유시간이다.
이 경우 철수는 사건이 일어나는 장소인 A지점과
상대속도를 갖는 관성계에 있으므로
철수가 측정한 두 사건 사이의 시간간격은 '팽창시간'이고
무조건 고유시간보다 크게 측정된다.
그럼 영희 입장에서 철수의 시간은 빨리 갈까?
아니다.
영희 입장에서는
철수가 왼쪽 방향으로 v의 속력으로 움직이는것으로 보일것이기 때문이다.
영희가 오른쪽 방향으로 v의 속력으로 움직이는건
철수의 입장에서 봐서 그런거지
절대적인게 아니다.
그냥 관찰자입장에서
난 정지해있다. 근데 주변의 모든게 움직이는거다 라고 생각하면 된다.
이해 했는지 간단한 문제로 물어보겠다.
A가 우주선을 타고 있다.
B가 보기에 우주선은 v의 속력으로 운동하고있다.
A가 보기에 B의 시간은 느리게 가는가? 예.
B가 보기에 A의 시간은 느리게 가는가? 예.
A가 보기에 우주선이 v의 속력으로 움직일때와
A가 보기에 우주선이 3v의 속력으로 움직일때
A가 관측할때 B는 어느 쪽이 더 시간이 느리게 가는가? 3v로 움직일때.
A와 B 중 누구의 시간이 더 느리게 가는가? 잘못된 문제.
하나라도 틀렸으면 이해 못한거니까 다시읽자
- 시간팽창 간단요약 -
상대속도가 있으면 쟤가 나보다 시간이 느리게 간다.
관찰자에 대해 움직이는 관성계에서의 사건의 시간을 측정하면 고유 시간보다 길어진다.
- 길이 수축 -
관찰자와 다른 속도로 운동하는 물체의 길이는
운동방향으로 짧아진다.
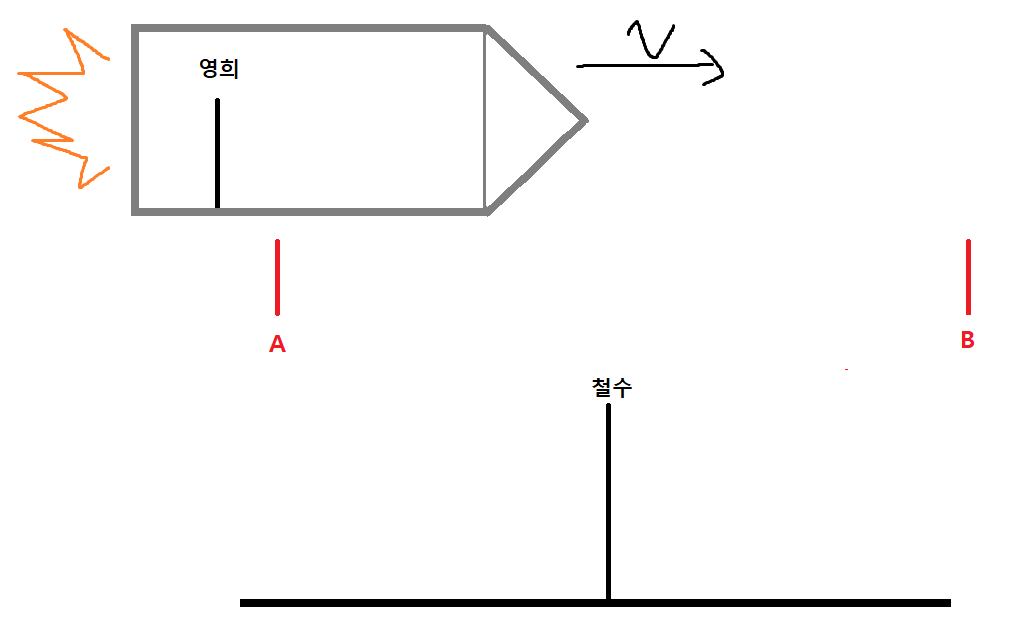
이번엔 영희가 탄 우주선이 A지점부터 B지점까지 운동한다고 해보자.
철수 입장에서 A지점과 B지점은 정지해있고
영희 입장에서 B 지점은 자신에게 v의 속력으로 다가오고있다.
- 고유 길이 -
사건이 일어나는 곳과 같은 운동 상태인 관찰자가 측정한 길이가 고유길이 이다.
예를 들자면
여기서 철수가 측정한 길이가 고유길이 이다.
-철수가 측정한 길이-
우선 철수 입장에서 측정하려는 것은
1. 우주선이 A를 지나는 사건
2. 우주선이 B를 지나는 사건
그리고 그 두 사건 사이의 시간간격과 거리
근데 철수 입장에서 보면
두 사건은 같은 장소에서 일어나지 않았다.
A와 B는 어느정도 떨어져서 멈춰있었기 때문에
따라서 이때 철수가 측정한 시간을 t(철수), 길이를 L(철수)라 하면
L(철수) = vt(철수)
L(철수) : 고유길이, t(철수) : 팽창시간
-영희가 측정한 길이-
영희 입장에서는
자신은 가만히 있는데
B지점이 자신에게 다가오고있다.
A지점이 우주선을 지나는 사건
B지점이 우주선을 지나는 사건
이 두 사건이 우주선이라는 같은 장소를 지나갔다.
따라서 이때 영희가 측정한 시간이 고유시간이다.
따라서 이때 영희가 측정한 시간을 t(영희), 길이를 L(영희)이라 하면
L(영희) = vt(영희)
근데 t(영희)는 고유시간이므로 t(영희)<t(철수)
따라서 L(영희)<L(철수) 이고
L(철수)은 고유길이이므로
길이 수축이 증명되었다.
그리고 우주선 자체의 길이도 수축된다.
우주선의 길이를 재기 위해
우주선 왼쪽 끝지점과 오른쪽 끝지점의 간격을 구한다.
아까와 같은 논리를 적용하자.
영희가 잰 우주선의 길이는 고유길이이다.
재고자 하는 두 지점과의 상대속도가 0이니까.
철수가 잰 우주선의 길이는
재고자 하는 두 지점이 자신에 대해 상대속도를 갖고 있으므로
영희가 잰 것(고유길이)보다 짧다고 측정할것이다.
-오개념 주의-
여기서 영희 입장에서
철수의 시간이 영희의 시간보다 느리게 가므로
t(영희)>t(철수) 라는 논리가 들어오면 안된다.
즉 시간의 빠름과 느림으로
시간간격의 대소관계를 비교하려 들면 안된다.
그러면 L(영희)>L(철수)라는
길이가 오히려 팽창한다는 이상한 결론이 나온다.
이게 왜틀렸냐면
'동시성의 상대성' 때문에 그렇다.
우선 '시간 팽창'에 의해 영희 입장에서 철수의 시간이 느리게 가는건 맞다.
근데 그걸로 '시간 간격'의 크기를 비교하면 안된다.
쉽게 말해서
'우주선이 A지점, B지점에 도달하는 순간'은
동시성의 상대성 에 의해
철수와 영희에게 동시에 관측되지 않는다.
왜냐면 철수와 영희는 서로에 대한 상대속도가 있는 관성계에 있으니까
엄밀히 따지자면
A지점에 도달하는 순간은
철수에게 먼저 관측될것이고
B지점에 도달하는 순간은
영희에게 먼저 관측될것이다
따라서 t(철수)>t(영희)이다.
시간 간격을 잴때
우주선이 A지점, B지점에 도달하는 순간이
동시에 관측된다고 가정하고 논리를 전개했으므로
저런 오개념이 나오는것이다.
길이 수축은 운동 방향으로만 일어나며, 수직 방향으로는 일어나지 않는다.
아까와 같은 상황인데 이번엔
우주선의 높이를 각각 측정했다고 해보자.
우주선의 높이는 운동 방향과 수직이다.
측정하려는 것과 운동방향이 수직이므로
수직방향 상대속도는 0이고
따라서 길이 수축이 일어나지 않는다.
요약하면
움직이는 것의 길이를 측정하면 고유길이보다 짧게 나온다.
길이는 운동 방향으로만 수축된다.
- 특수 상대성 이론의 검증 -
우주선이 공기 분자와 충돌하면 생기는 '뮤온' 이라는 입자가 있다.
이 입자의 수명은 약 2µs = 0.00002초 이다.
수명이 매우 짧아 지표면에 도달할수 없다.
따라서 지표면에서 관측하기 매우 힘들것이다.
근데 실제로는 지표면에서 뮤온이 관측된다.
뮤온은 광속에 가까운 초고속으로 움직이기 때문에
여기서의 2µs라는 수명은 뮤온 입장에서의 고유시간이고
지표면의 관측자이 이 뮤온을 관측하면
시간팽창이 일어날것이므로
뮤온의 수명이 2µs보다 큰 것으로 보인다.
즉 이론상 거의 관측될수 없는 '뮤온'이라는 입자가
실제로 지표면에서 관측되는 걸로 보아
특수상대성 이론에 의해 시간팽창으로 뮤온의 수명이 길어진걸로 관측하기 때문이다.
- 질량-에너지 동등성 -
질량과 에너지는 서로 전환될 수 있으며,
정지질량 m0_인 물체가 가지는 에너지는
E=m0_c²이다. 여기서 E를 정지에너지라 한다.
- 질량의 상대성 -
물체의 속력이 증가하면 상대론적 질량도 증가한다.
즉 정지질량보다 커진다.
질량 쪽은 별로 안중요하니
정지에너지 E=m0_c² , 속력증가하면 질량증가
이정도로만 알고 적당히 읽고 넘어가자
평가원에서 딱 한번 양성자의 정지에너지는 0인가? 라고 물은 적이 있는데
양성자의 정지질량 m0_>0이고
정지에너지는 E=m0_c²이라서 틀린말이다.
- 요약-
특수 상대성 이론 : 시간, 공간은 상대적이고
절대적인 기준은 '빛의 속력'이다.
진공에서 진행하는 빛의 속력은 언제 어디서 어떻게 재든 항상 같다.
시간 팽창 : 상대속도가 있으면 쟤가 나보다 시간이 느리게 간다.
시간팽창이 일어나므로 고유시간<팽창시간 이다.
길이 수축 : 상대속도가 있으면 원래 길이보다 짧게 측정된다.
고유길이>수축길이 이다.
- 예제 -
처음엔 대체 무슨말인가 하나도 이해 안되고 어려울텐데
감을 잡으면 쉽다.
그래도 문제 자주 풀어서 감을 유지해주지 않으면
수능때 헷갈려서
킬러문제 잘 풀어놓고 이런데서 틀리는
소위 말하는 '의문사' 할 수 있으니 문제를 많이 풀어봐야한다.
1 )
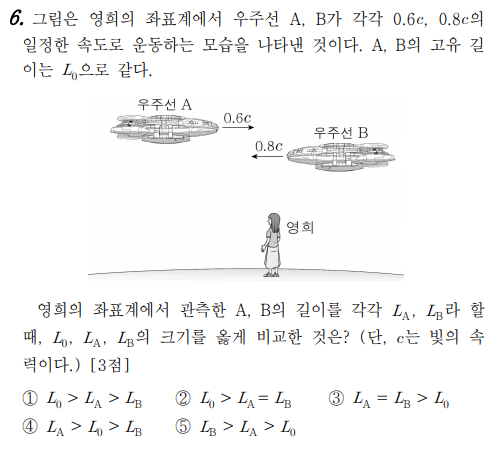
-문제풀이 단서-
A, B의 고유길이가 같다.
영희의 좌표계에서 보면
A,B는 길이 수축이 일어난다.
따라서 L0_>La_ , L0_>Lb_ 이다.
그리고 영희의 좌표계에서 B가 A보다 빠르게 움직이고 있으므로
B가 더 길이수축이 많이 일어난다.
따라서 La_>Lb_이고 답은 1번
2 )

-문제풀이 단서-
두 우주선의 고유 길이는 같다.
ㄱ)
'광속 불변의 법칙' 에 의해
레이저 광선(빛)의 속력은 항상 일정하다.
따라서 ㄱ(x)
ㄴ)
A가 보기에
B가 C보다 빨리 움직이고 있다.
즉 길이 수축은 B가 더 많이 되었다.
근데 둘의 고유길이가 같으므로
길이 수축이 더 많이된 B가 더 짧게 측정될것이다.
따라서 ㄴ(o)
ㄷ)
A가 보기에
B는 0.6c의 속력으로
C는 0.3c의 속력으로 다가오고 있다.
따라서 시간 팽창은 B가 더 많이 일어난다.
따라서 A가 보기에 B의 시간이 C의 시간보다 느려보인다.
따라서 ㄷ(x)
답은 1번
3 )

-문제풀이 단서-
1. 우주선 내부는 진공이다.(=광속불변의법칙을 적용해도 된다)
ㄱ)
p와 q는 우주선 내부에 있다.
따라서 p와 q 사이의 거리는
영희가 측정한게 고유 길이다.
따라서 철수가 측정한 거리가 더 짧다.
따라서 ㄱ(x)
ㄴ)
진공에서 빛의 속력은 항상 일정하다.
따라서 ㄴ(o)
ㄷ)
광속 불변의 법칙에 의해
영희가 측정한 빛의 속력 = 철수가 측정한 빛의 속력
특수상대성 이론 문제는
고유시간과 고유길이를 찾는게 풀기 쉽다.
이걸 기준으로 보면 되니까
여기서 저 빛이 왕복하는 사건에 대한
고유 시간은 우주선에 타고있는 영희가 측정한 시간이다.
따라서 철수가 측정할때는 시간팽창이 일어났다.
빛의 이동거리 = 빛의 속력 x 이동시간
따라서 철수가 측정한 이동거리 > 영희가 측정한 이동거리
따라서 ㄷ(x)
따라서 답은 2번
길이 수축이 일어났으므로 철수 < 영희가 아닐까? 할수 있는데
길이 수축이 일어난건 맞다. 근데
p에서 방출된 빛이 q에 도달하는 시간 ≠ q에서 반사된 빛이 p에 도달하는 시간 이다.
왜냐면 빛 입장에서 q는 0.8c의 속력으로 도망가고있고
p는 0.8c의 속력으로 다가오고있기 때문이다.
여기서 철수측정 빛의 이동거리 > 영희관측 빛의 이동거리 인것을
굳이 증명을 해보자면 할순 있지만
수능에서는 이정도 수준을 요구하지 않는다.
방금 풀이가 받아들이기 어렵다면 한번쯤 해보는건 나쁘지 않다.
p에서 방출된 빛이 p로 되돌아오는 시간간격을
영희가 측정한걸 t,
철수가 측정한걸 T라 하겠다.
고유 시간은 우주선에 타고있는 영희가 측정한 시간이다.
따라서 영희가 측정한 거리는 2ct이다.
철수가 측정한 거리는
빛이 p에서 q까지 가는 시간을 T₁
q에서 p까지 가는 시간을 T₂ 라 측정했다고 해보자.
그럼 T₁+T₂ = T 이고
철수가 측정한 거리는
(c-0.8c)T₁ + (c+0.8c)T₂ 이고
정리하면 0.2cT₁ + 1.8cT₂ 이다.
이제 2ct와 0.2cT₁ + 1.8cT₂ 의 크기를 비교하면 된다.
만약 2ct = 0.2cT₁ + 1.8cT₂ 라면
ㄷ은 맞는 선지가 된다.
2ct = 0.2ct + 1.8ct니까 보기 편하게 다시 쓰면
0.2ct + 1.8ct = 0.2cT₁ + 1.8cT₂ 이다.
근데 T는 팽창시간이다.
그리고 T = T₁ + T₂ 이다.
따라서 0.2ct < 0.2cT₁ 이고
1.8ct < 1.8cT₂ 이므로
0.2ct + 1.8ct < 0.2cT₁ + 1.8cT₂ 이다.
따라서 ㄷ은 틀린 선지이다.
4 )

-문제풀이 단서-
광원 P에서 발생한 빛은 '영희'가 측정하였을때 A,B에 동시도달하였다.
ㄱ)
철수 입장에서 영희는 왼쪽 방향 0.5c의 속도로 운동중이다.
따라서 영희의 시간이 철수의 시간보다 느리게 간다.
따라서 ㄱ(o)
ㄴ)
철수가 측정할때 P에서 발생한 빛은
B보다 A에 먼저 도달하는가?
영희가 측정할때 A와 B에 동시도달 했다 하는데
광원에서 발사된 빛이 A,B를 향해 간다고 해보자.
빛 입장에서 A는 다가오고 있고
B는 도망가고 있다.
따라서 P에서 발생한 빛이
'영희가 보기에' 동시도달하려면
P에서 A까지의 거리가
P에서 B까지의 거리보다 멀어야 한다.
따라서 철수가 측정할때
P에서 발생한 빛은
P에서 B까지의 거리가 더 가까우므로 B에 먼저 도달한다.
따라서 ㄴ(x)
ㄷ)
A, P, B는 영희에 대해 같은 속도로 움직이고있다.
따라서 A-P와 B-P는 같은 비율만큼 길이가 수축될것이다.
근데 A-P 거리가 B-P거리보다 크다.
따라서 영희 입장에서는 A-P B-P 둘다 길이수축이 되었지만
A-P 거리가 더 크다고 볼것이다. 따라서 ㄷ(x)
따라서 답은 1번
5 )

-문제풀이 단서-
1. B의 관성계에서 광원과 거울 사이의 거리는 L이다.
2. 빛의 방출 방향은 우주선의 운동방향과 수직이다.
ㄱ)
진공에서 빛의 속력은 무조건 c이다.
따라서 ㄱ(o)
이거는 선지 하나를 공짜로 주는 수준의 난이도라
절대 틀리면 안되고 만약 틀렸으면 공부 다시해야된다.
ㄴ)
A의 관성계에서 광원과 거울 사이의 거리는 L인가?
B가 측정한 거울과 광원 사이의 거리는 L인데
여기서 A가 보기에 길이수축이 일어났냐고 묻는 선지이다.
근데 L은 운동방향과 수직이다.
수직방향 길이수축은 일어나지 않는다.
따라서 ㄴ(o)
ㄷ)
이것도 사실상 선지 하나 공짜로 주는 수준의 난이도이다.
'상대속도가 있으면 쟤가 나보다 시간이 느리게 간다'
ㄷ(x)
따라서 답은 3번
6 )

-문제풀이 단서-
1. A가 측정할때 광원에서 발생한 빛이 P,Q,R에 동시도달하였다.
2. B가 측정한 각각의 광원으로부터의 거리는 Lp_, Lq_, Lr_이다.
ㄱ)
우선 B에서 측정한 길이가 고유길이이다.
따라서 A가 측정한 P와 Q 사이의 거리는
길이 수축에 의해 Lp_+Lq_ 보다 작을것이다.
따라서 ㄱ(o)
ㄴ)
A가 측정할때 광원에서 발생한 빛이 P,Q,R에 동시도달하였다.
빛 입장에서 보면
P : 다가오고 있음
Q : 도망가고 있음
R : 가만히 있음
따라서 A가 측정할때 P,Q,R에 빛이 동시도달하려면
Lp_>Lr_>Lq_ 여야한다.
따라서 ㄴ(x)
참고로 R과 광원은 운동방향과 수직이기 때문에
길이 수축이 일어나지 않는다.
ㄷ)
상대속도가 있으면 무조건 쟤가 나보다 시간이 느리게 간다고 했다.
따라서 ㄷ(x)
따라서 답은 1번
7 )

-문제풀이 단서-
1. P의 관성계에서 Q가 P를 스쳐지나가는순간 A,B가 동시에 빛을 냈다.
2. P에 대해 A,B는 같은 거리만큼 떨어져있다.
ㄱ)
A와 P의 거리와
B와 P의 거리는 같으므로
당연히 ㄱ(o)
ㄴ)
Q는 B쪽으로 운동하고 있으므로
B에서 방출된 빛이 먼저 도달한다.
따라서 Q의 관성계에서는
B가 A보다 먼저 폭발했다고 관측할것이다.
따라서 ㄴ(o)
ㄷ)
Q의 관성계에서
A, P, B는 모두 왼쪽방향 0.9c의 속도로 운동하고있다.
따라서 A-P 길이수축과 B-P 길이수축의 비율은 같다.
근데 A-P 길이와 B-P 길이가 같으므로
Q의 관성계에서 재도
A-P 길이와 B-P 길이는 같을것이다.
물론 A-P와 B-P 길이 자체는 수축될것이다.
따라서 ㄷ(x)
따라서 답은 3번
8 )

-문제풀이 단서-
P의 관성계에서의 사건이 서술되어있다.
개인적으로 수능에서 특수상대성이론 문제가 어렵게 나와봐야
이것보다 조금 어려운 수준에서 그칠거라 생각한다.
ㄱ)
뭔가 복잡하게 설명해놨는데 천천히 보자.
P의 관성계에서
Q가 P를 지나는 순간
Q에서 거리가 같은 A와 B에서 동시에 빛이 발생되었다.
따라서 P에서 A까지의 거리와
P에서 B까지의 거리는 같다.
따라서 동시에 발생한 빛이
같은 거리만큼 올것이므로
빛은 동시에 P에 도달한다.
따라서 ㄱ(o)
ㄴ)
P의 관성계에서 A, B에서 동시에 빛이 방출되었다.
A, B에서 방출된 빛의 입장을 들어보자.
A빛 : Q는 0.5c의 속력으로 도망가고있다.
B빛 : Q는 0.5c의 속력으로 다가오고있다.
근데 P의 관성계에서
A-Q 거리와 B-Q 거리는 같다고 측정했으므로
Q가 다가오고 있는 B빛이 더 빨리 Q에 도달할것이다.
즉 B에서 발생한 빛이 먼저 Q에 도달한다.
따라서 ㄴ(x)
ㄷ)
B에서 발생한 빛이 Q에 도달할 때까지 걸리는 시간은
Q의 관성계에서가 P의 관성계에서보다 큰가?
우선 'Q의 관성계'에서 B-Q의 거리를 측정하면
그게 고유길이다.
이걸 L이라 하겠다.
그럼 B에서 발생한 빛이 Q에 도달할때까지 걸리는 시간은 L/c이다.
다음으로 'P의 관성계'에서 B-Q의 거리를 측정하면
그건 수축길이다.
이걸 L'이라 하겠다.
그럼 B에서 발생한 빛이 Q에 도달할때까지 걸리는 시간은
L'/(c+0.5c)이다.
왜 L'/c 가 아니라 L'/(c+0.5c)냐면
빛 입장에서 Q는 자기에게 0.5c의 속도로 다가오고 있기 때문이다.
L'<L이므로
(Q의 관성계 시간) L/c > (P의 관성계 시간) L'/(c+0.5c)
따라서 B에서 발생한 빛이 Q에 도달할 때까지 걸리는 시간은
Q의 관성계에서가 P의 관성계에서보다 크다.
따라서 ㄷ(o)
따라서 답은 4번
'물리I > I. 역학과 에너지' 카테고리의 다른 글
| 특수 상대성 이론 #2 - 질량과 에너지 (1) | 2021.08.05 |
|---|---|
| 에너지와 열 #2 - 열역학 법칙과 열기관 (0) | 2021.07.28 |
| 에너지와 열 #1 - 일과 에너지, 역학적 에너지 보존 (1) | 2021.07.22 |
| 힘과 운동 #4 - 운동량 보존 법칙과 충돌 (0) | 2021.07.17 |
| 힘과 운동 #3 - 뉴턴 운동 법칙 (0) | 2021.07.16 |



