평가원이 건드리지 않다가
돌림힘과 유체역학을 통째로 삭제하고나서 킬러 낼게 없으니
최근에 평가원이 킬러급으로 문제를 출제하기 시작했다.
- 마찰 전기 -
종류가 다른 두 물체를 마찰시키면
전자가 한 물체에서 다른 물체로 이동하는데,
전자를 잃은 물체는 양(+)전하를 띠고
전자를 얻은 물체는 음(-)전하를 띤다.
이때 물체가 전기를 띠는 현상을 '대전'이라 하고,
전기를 띤 물체, 즉 대전된 물체를 '대전체'라 한다.
이 내용은 당장 전기력문제엔 안나오지만
뒤쪽 단원에 자주 나오는 내용이니 알아두도록 하자.
- 전하 -
대전체가 띠고 있는 전기를 전하라고 하며,
전하의 량을 전하량이라고 한다.
기본 전하량은 전자의 전하량(e)의 크기인 1.6x10^-19 C 이다.
C는 coulomb이고 쿨롱 또는 쿨롬 이라고 읽는다.
1C은 전류 1암페어가 1초 동안 흘렀을 때 이동한 전하의 양이다.
전하량 보존 법칙 : 임의의 고립된 계 내의 모든 전하의 대수적인 합은 언제나 일정하다.
쉽게 설명하자면
고립된 계 : 외부와의 상호작용이 없다.
대전체 A와 B가 있는 고립된 계가 있다고 하고
A의 전하량을 +2Q, B의 전하량을 +4Q라 하면
이 계의 전하량의 합은 +6Q로 항상 일정하다.
예를 들어
+2Q인 물체와 +4Q인 물체가 접촉하면 둘다 +3Q가 된다.
+2Q인 물체와 -4Q인 물체가 접촉하면 둘다 -Q가 된다.
-2Q인 물체와 +6Q인 물체가 접촉하면 둘다 +2Q가 된다.
이것도 당장 전기력문제엔 안나오지만
뒤쪽 단원 문제를 풀기 위해 알아야 하는 내용이니 알아두자.
- 전기력 -
전하를 띤 물체 사이에는 힘이 작용한다.
이를 전기력이라 한다.
같은 종류의 전하 사이에는 미는 힘(척력)
다른 종류의 전하 사이에는 당기는 힘(인력)
이 작용한다.
작용-반작용 법칙에 의해 당연히 서로에게 가하는 힘은 같다.
전하량 +2Q인 물체와 전하량 -Q인 물체는 서로 당기는 힘(인력)이 전기력으로써 발생한다.
전하량 +Q인 물체와 전하량 +3Q인 물체는 서로 미는 힘(척력)이 전기력으로써 발생한다.
- 점전하 -
부피가 없고 전하량만 갖고 있는 이론적 존재이다.
그냥 전하가 모여있는 '점'이라고 생각하면 된다.
여기에서의 점은 'dot'가 아니라 'point'이다.
사실 1단원에서 물체의 운동을 기술하거나 문제풀이 할때도
질량체는 거의 다 점질량이었다.
문제에서는 이를 '단, 물체의 크기는 무시한다' 라는 문장으로
점질량이니까 크기 생각하지말고 풀라고 알려준다.
쉽게 설명해서
'점전하' 라는 단어가 등장하면
크기는 생각하지 않아도 되겠구나 하면 된다.
- 쿨롱 법칙 -
두 전하 사이에 작용하는 힘을 전기력이라 했는데
이 전기력의 크기를 나타내는 것이 바로 쿨롱 법칙이다.
1. 두 점전하 사이의 전기력은 각 전하량의 곱에 비례한다.

2. 두 점전하 사이의 전기력은 거리의 제곱에 반비례한다.

둘을 합친다음 비례 상수를 넣으면 등식으로 나타낼수 있다.

q1, q2가 전하량이랬지 전하량의 크기라고 안했으므로
F가 음수가 나올수도 있다.
- 심화 : 전기력의 합 -

x축 위에
점전하 A, B, C가 고정되어 있다고 해보자.
이때 B는 A와 C에 의해
전기력을 받을것이다.
이때 B가 받는 전기력의 합력을 0이라고 해보자.
그리고 A는
B와 C에 의해 -x방향 전기력 F를 받는다고 해보자.
그럼 C가
A와 B에 의해 받는 전기력의 방향과 세기는?
이건 작용반작용 법칙의 심화과정이다.
왜냐면 A+B+C를 하나의 '계'로 본다면
계 밖에서는
A,B,C에 아무짓도 안했기 때문에
결론적으로 A,B,C가 서로 주고받는 전기력은
A+B+C를 하나의 계로 본다면
A+B+C 라는 계에 가하는 전기력이 0이기 때문에
A+B+C 라는 계가 받는 전기력은 0이다.
결국 A,B,C가 서로 주고받는 전기력을
모두 더해주면 0이 나올것이다.
즉 A, B, C의 전기력의 총합은 0이다.
따라서 C가 받는 전기력은
B가 받는 전기력 0
A가 받는 전기력 -x방향 F
따라서 전기력의 총합이 0이 되기 위해
C가 받는 전기력은 +x방향 F이다.
- 예제 -
진짜 내용이 이게 끝이다.
근데 문제는 어렵게 나온다.
근데 다 전하량보존법칙이랑 쿨롱법칙 쓰면 답이 나온다.
1 )

우선 (가)에서 B가 정지해 있을 수 있으려면
A가 B에게 작용하는 힘과 C가 B에게 작용하는 힘이 힘의 평형 관계여야 한다.
따라서 A가 B를 당기고 있으면 C도 B를 당겨야하고,
A가 B를 밀고있으면 C도 B를 밀어야한다.
따라서 A와 C의 전하의 종류는 같다.
쉽게 말해서 만약 A가 +면 C도 +여야한다.
ㄱ)
(나) 같은 상황을 쉽게 푸는법을 알려주겠다.
A를 B에서 멀리 하였다 했지
얼마나 멀리했다고 했는지는 안알려줬다.
따라서 1cm 멀리 떨어트리나
100000000cm 멀리 떨어트리나
B가 C쪽으로 기울어져서 정지했다는건 같다.
그럼 무한히 멀리 떨어트리면 어떻게 될까?
A가 B에 작용하는 힘이 거의 0에 가까워질것이다.
따라서 A를 무한히 멀리 떨어트렸다고 하면
B와 C만 있는 상황이라고 봐도 된다.
즉 (가)의 상황에서 A를 없애버린게 (나)의 상황이다.
A를 없애버렸더니 B가 C를 향해 기울었다고 했으니
B와 C는 서로 당기는 힘(인력)이 작용하고있다.
따라서 B와 C는 대전된 전하의 종류가 다르다.
따라서 ㄱ(o)
ㄴ)
(가)에서 쿨롱 법칙을 적용해보자.
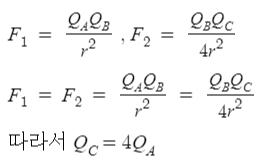
따라서 ㄴ(o)
ㄷ)
(가)의 상황에서 B가 정지해 있으려면
C가 B를 당기고 있으니
A도 B를 당겨야한다.
즉 인력이 작용해야한다.
따라서 ㄷ(x)
따라서 답은 3번
2 )

A와 C가 B에 작용하는 전기력이 0이다 =
A가 B에 작용하는 전기력의 크기 = C가 B에 작용하는 전기력의 크기
이에 쿨롱법칙을 적용하여 수식을 쓰면
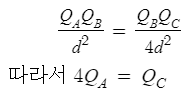
앞으로 편의상 Qa_를 q라 놓겠다.
그럼 Qc_는 4q가 된다.
B가 A에 작용하는 전기력의 크기 < C가 A에 작용하는 전기력의 크기
이에 쿨롱법칙을 적용하여 수식을 쓰면

따라서 답은 4번
3 )

-문제풀이 단서-
1. A, B, C는 같은 거리만큼 떨어져있다.
2. A는 양전하이고 작용하는 전기력은 0이다.
3. B에 작용하는 전기력은 -x 방향이다.
ㄱ)
우선 A에 작용하는 전기력이 0이려면
B가 A를 밀었다면
C는 A를 같은 힘만큼 당겨야한다.
즉 B와 C의 전하의 종류가 반대여야한다.
따라서 B가 +면 C는 -
B가 -면 C는 +전하여야 한다.
근데 B에 작용하는 전기력의 방향이 -x방향이다.
만약 B가 +전하고 C가 -전하라면
A가 B를 밀고 C가 B를 당기기때문에
+x방향의 전기력이 작용해야한다.
근데 B에 작용하는 전기력의 방향은 -x라 했으므로
B는 -전하, C는 +전하이다.
따라서 ㄱ(o)
ㄴ)
A, B, C의 전하의 종류를 정리하면
A : + , B : - , C : +
즉 B에 작용하는 전기력은
A가 B를 당기는 힘
C가 B를 당기는 힘
근데 -x방향의 전기력이 작용했다는건
A가 B를 당기는 힘 > C가 B를 당기는 힘 이라는 뜻이다.
따라서 전하량의 크기는 A가 C보다 크다.
따라서 ㄴ(x)
ㄷ)
두가지 방법으로 풀어줄건데
두번째 방법이 압도적으로 빠르지만
첫번째 풀이도 알아두면 좋기때문에
둘다 적어놓았다.
- 첫번째 풀이 -
우선 A에 작용하는 전기력이 0이므로
B가 A를 당기는 힘 = C가 A를 당기는 힘
A와 B 사이의 거리를 r이라 하면
A와 C 사이의 거리는 2r이 되고
이를 쿨롱법칙을 이용해 수식을 쓰면
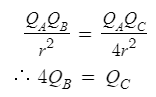
여기서 잠깐
B는 음전하고 C는 양전하인데
어떻게 4Qb_ = Qc_라는 식이 가능할까?
내가 식을 세울때 Qa_, Qb_, Qc_를
A, B, C 각각의 전하량의 크기 라고 하고
식을 세워서 그렇다.
1단원 하고왔으니 이정도는 쉽게 이해할거라 믿는다.
여기서도 아까 1번 예제의 ㄱ선지를 풀때와 같은 논리를 적용해보자.
A에 작용하는 전기력은 0이라 했고
여기서 쿨롱법칙을 이용해서
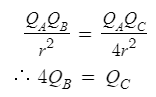
인걸 알았다.
여기서 중요한건 A에 작용하는 전기력이 0인거랑
A의 전하량의 크기는 아무 관계가 없다.
왜냐면 둘다 쿨롱법칙쓴다음 둘이 같다고 식을 썼으니
Qa_는 어차피 약분될거기 때문이다.
그리고 B에 작용하는 전기력의 방향이 -x라 했지
전기력의 크기는 알려주지 않았다.
즉 전기력의 방향이 -x기만 하면
B에 작용하는 전기력의 크기는 상관없고
따라서 A의 전하량의 크기는 몇으로 놓든 상관없다.
아까처럼 A의 전하량의 크기를 말도안되게 크다고 가정해버리자
그러면 C에 작용하는 전기력은
A가 C를 미는힘
B가 C를 당기는힘인데
A의 전하량의 크기가 B보다 아득히 크므로
A가 C를 미는 힘이 압도할것이다.
따라서 C에 작용하는 전기력의 방향은 +x방향이다.
따라서 ㄷ(x)
- 두번째 방법 -
전기력의 총합은 0이기때문에
A가 받는 전기력 0
B가 받는 전기력 -x방향
따라서 C가 받는 전기력은 +x방향이며
B가 받는 전기력과 크기가 같다.
따라서 ㄷ(x)
따라서 답은 1번

이건 답지풀이인데 내 풀이가 꼼수같아서 시원찮으면 같이 보도록 하자.
4 )

-문제풀이 단서-
1. (가) 상황에서 A, B, C는 같은 간격으로 놓여있다.
2. (가) 상황에서 A에 작용하는 전기력은 0이다.
3. (가)의 C를 -x방향으로 옮겼더니 B에 작용하는 전기력이 0이 되었다.
ㄱ)
(나)에서 B에 작용하는 전기력이 0이라는건
A가 B에 작용하는 전기력의 크기와
C가 B에 작용하는 전기력의 크기가 같다는것이다.
따라서 A가 B를 밀었으면
C도 B를 밀어야하고
A가 B를 당겼으면
C도 B를 당겨야한다.
따라서 A와 C의 전하의 종류는 같고
A가 양전하이므로 C도 양전하이다.
따라서 ㄱ(o)
참고로 선지에서 묻지는 않았지만
A와 C가 둘다 양전하이므로
(가)에서 A에 작용하는 전기력이 0이려면
C가 A를 미는 힘을 상쇄할 정도의 당기는 힘이 필요하고
따라서 B는 음전하이다.
ㄴ)
아까와 같은 논리로
C를 B와 아주 가깝게 붙였다고 해보자.
그러면 B에 작용하는 전기력이 0이기 위해
A의 전하량이 C의 전하량보다 아득히 커야한다.
그리고 (가)에서 A에 작용하는 전기력이 0인데
B가 C보다 가까이 있으므로
Qc_ > Qb_인걸 알 수 있다.
근데 아까 Qa_>>Qc_라 했으므로
Qa_>>Qc_>Qb_이고
따라서 전하량의 크기는 B가 A보다 작다.
따라서 ㄴ(x)
ㄷ)
(가)에서 C에 작용하는 전기력은
A가 C를 미는 힘
B가 C를 당기는 힘
Qa_>>Qc_>Qb_라 했으므로
C에 작용하는 전기력은
어차피 A가 C에 작용하는 전기력이 압도한다.
A와 C는 둘다 양전하이므로 서로 미는 힘이 작용할것이고
따라서 C에는 +x방향의 전기력이 작용한다.
따라서 ㄷ(x)
따라서 답은 1번

이건 답지풀이인데
이쯤 되면 내가 자꾸 A전하량이 C전하량보다 '압도적으로' 크다거나
A를 '무한히' 멀리 떨어트린다거나 하는 이유를 이해할수 있다.
그냥 상황을 이해하기 쉽게 설명해주는것이다.
5 )

-문제풀이 단서-
전기력의 방향과 크기가 제시되었다.
일단 A와 B가 양전하인지 음전하인지 찾아야 뭘 할 수 있을거같다.
따라서 A, B의 전하의 종류부터 찾아볼것이다.
(가)와 (나)의 상황을 비교해보자
(가)와 (나)에서 B가 C에 작용하는 전기력은 같을것이다.
B와 C는 여기서 변한게 없으니까
A만 C 오른쪽로 옮겼더니 +x방향으로 더 큰 전기력을 받은 상황이다.
근데 B에 작용하는 전기력이
(나)에서 더 커졌다.
따라서 (가)에서는 A가 C에게 작용하는 전기력이 -x방향이고
(나)에서는 A가 C에게 작용하는 전기력이 +x방향이다.
따라서 A는 C를 당기고있다.
따라서 A는 음전하고
(가)에서 C가 +x방향 전기력을 받기 위해서는
B가 양전하여야한다.
따라서 B는 양전하다.
이제 전하의 종류를 모두 알았으니
각각의 점전하가 가하는 전기력의 방향을 알수있다.
각각의 전기력들이 서로 상쇄시키는 반응인지, 보강시키는 반응인지 알수있다는 뜻이다.
쉽게 예를 들자면
(가) 상황에서 C에 작용하는 전기력은
+x를 양의 방향으로 잡으면
A가 C에 작용하는 전기력은 -x방향이므로 -부호
B가 C에 작용하는 전기력은 +x방향이므로 +부호를 넣으면 된다.
2F = ( B가 C에 작용하는 전기력 ) - ( A가 C에 작용하는 전기력 )
이런식으로.
A, B, C의 전하의 크기를 각각 Qa_, Qb_, Qc_라 놓고
(다)에서 A에 작용하는 힘을 Fa_라 놓고
쿨롱 법칙을 이용해 수식을 쓰면

따라서 답은 3번

답지의 풀이는 이런식으로 나와있는데
결국 둘다 똑같은 풀이이다.
편한걸로 쓰자.
'물리I > II. 물질과 전자기장' 카테고리의 다른 글
| 전자기장 #2 - 물질의 자성 (0) | 2021.08.13 |
|---|---|
| 전자기장 #1 - 전류에 의한 자기장 (0) | 2021.08.12 |
| 물질의 구조와 성질 #4 - 반도체와 다이오드 (0) | 2021.08.10 |
| 물질의 구조와 성질 #3 - 고체의 에너지띠와 전도성 (0) | 2021.08.10 |
| 물질의 구조와 성질 #2 - 빛의 흡수와 방출 (0) | 2021.08.09 |



