
- 개요 -
제목 그대로, 어떤 두 직선의 교점을 지나는
직선의 방정식을 구해볼것이다.
그리고 미지수가 포함된 어떤 직선의 방정식에서,
미지수의 값에 상관없이 그 직선이 무조건 지날수밖에 없는 점이 있는데
그것도 구해볼것이다.
- 두 직선의 교점을 지나는 직선의 방정식 : 연립 풀이법 -

이런문제를 풀어볼것이다.
'교점'이라는게 뜻하는게 뭔가?
두 직선이 만나는 점을 교점이라 한다.
두 직선이 만난다는게 무슨뜻인가?
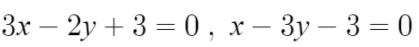
우선 이 두 직선은 둘다 교점을 지난다.
즉, 교점에서의 좌표를 저 직선의방정식에 대입하면 성립한다.
근데 두 직선이 둘다 교점을 지나므로
교점의 좌표를 저 두 직선의방정식중 아무데나 대입해도 성립한다는 뜻이고
이는 곧 연립방정식의 해를 의미한다.

따라서, 다음과 같은 결론을 얻는다.
교점 = 연립방정식의 해
그럼 이제 문제를 풀어볼까?

이 연립방정식의 해가 바로 교점의 좌표이다.
연립방정식 푸는건 중학생때도 했고 방정식 단원에서도 했으니 과정은 생략하겠다.
해를 구하면 x = -15/7 , y = -12/7
따라서 교점의 좌표는 ( -15/7, -12/7 ) 이다.
이제 이 점과 원점(0, 0)을 지나는 직선의 방정식을 작성하면 된다.
직선의 방정식 작성법도 이전에 했던거니 과정은 생략하겠다.
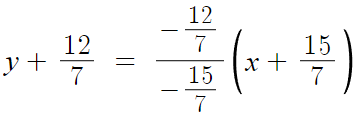
이를 정리하면 답은

혹시 -4x+5y=0 이라 구했다면 그것도 정답이다.
어차피 -1 곱하면 똑같은식이다.
- 두 직선의 교점을 지나는 직선의 방정식 : 다른 풀이법 -

이 문제를 또 풀어볼건데
사실 교점을 구해보지 않아도
두 직선의 교점을 지나는 직선의 방정식을 작성할 수 있다.
그리고 지금부터 설명할 풀이법이 사실 고등학교수학에서 원하는 정석풀이이다.
이건 아이디어가 필요하기 때문에 풀이법을 먼저 보여주고
어떻게 이렇게 되는지 설명해주겠다.

따라서 답은 (3x-2y+3) +k(x-3y-3) = 0 이다.
근데 여기서 끝내면 안되는게, 두 직선의 교점을 지나며
또다른 점인 원점(0, 0)을 지나는 직선은 하나밖에 없을것이므로
(0, 0)을 지나도록 하는 k값을 정해줘야한다.
따라서 (0, 0)을 위 식에 대입한다.
대입해서 계산해보면 k=1 이다.
따라서 답은 4x-5y=0 이다.

이게 대체 무슨말일까?
k값에 관계없다는건
k가 뭐든 무조건 교점을 지나야만 한다는건데
위에 세운 방정식은 두 직선의 방정식을 그냥 더한것 뿐인데
어떻게 항상 교점을 지나게 되는건가?
이것의 답은 우리가 처음에 풀었던 방법인 연립방정식 풀이법에 있다.
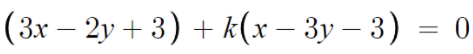
이게 k값에 상관없이 항상 성립하려면 어떻게 되어야할까?
간단하다. k값이 뭐든 상관없으려면
(x-3y-3)=0 이어서 k를 곱하면 0이 되게 해버리면 된다.
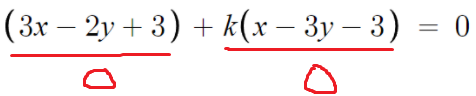
k(x-3y-3)=0 이므로
위 방정식을 항상 만족시키기 위해서는
(3x-2y+3) 도 0이어야한다.
즉, (x-3y-3)=0 과 (3x-2y+3)=0 을 동시에 만족해야한다.
(x-3y-3)=0 과 (3x-2y+3)=0 을 동시에 만족한다는건 곧 연립방정식의 해이고
이는 곧 (x-3y-3)=0 과 (3x-2y+3)=0 의 교점을 의미한다.
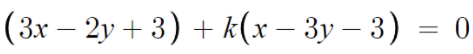
k의 값에 상관없이 지나는 점은
(3x-2y+3)=0 과 (x-3y-3)=0 을 동시에 만족하는 지점이므로
이 지점은 교점일수밖에 없는것이다.
여기서 주의할건, 이런 풀이를 적용하려면
직선의 방정식이 일반형이어야한다. 즉 ~~=0 꼴이어야 한다.
내가 전에 직선의 방정식을 작성할때 표준형이 더 쉽지만
일반형으로도 표현하고 이해할수 있어야한다고 했었는데
그 이유가 여기서 확실하게 나왔다.
요약하자면, 다음과 같다.

물론 방금 문제에선 (x-3y-3)에 k를 곱했지만
k값에 상관없는거라서 당연히 3x-2y+3에 k를 곱해도 된다.
- 어떤 직선이 항상 지나는 점 -

이런 문제를 풀어볼것이다.
사실 두 직선의 교점을 지나는 직선의 방정식 문제를 풀때와 다를게 없다.
대신 이번엔 반대로 교점을 구하는거다.
핵심논리 : k의 값에 관계없이 항상 지나는 점이 있다는건
이 점의 좌표를 대입하고 나면, k의 값에 관계없이 항상 성립한다는 뜻이고
이는 곧 k에 대한 항등식이라는 뜻이다.
아까 두 직선의 교점을 지나는 직선의 방정식을 구할때 썼던 논리를 그대로 쓸것이다.
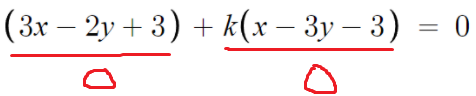
k에 곱해진것을 0으로 만들어버리면
k의 값에 관계없이 무조건 0이 된다. 이것을 이용할것이다.
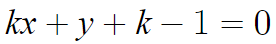
따라서 이 식은 조금 변형할 필요가 있다.
어떻게 변형할거냐면, k에 곱해진것을 0으로 만들거니까
k를 인수로 갖는 항들을 전부 묶어낼것이다.
쉽게 말해서, k에 대해 내림차순 정리하라는 말이다.
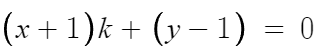
이런식으로 만들라는거다.
그러면 k의 값에 관계없이 항상 저 식이 성립하도록 하는 x와 y값을 구하면
거기가 바로 항상 지나는 점의 좌표이고 그게 답이다.
x+1=0 이면 (x+1)k는 무조건 0이다.
따라서 x=-1 이며,
0 + (y-1) = 0 이 항상 성립하려면 y=1 이어야한다.
따라서 x=-1, y=1이면 항상 성립한다.
따라서 저 직선은 항상 (-1, 1)을 지나며,
따라서 답은 (-1, 1)
- 예제 -
1 )

두 직선의 교점을 지나는 직선의 방정식을 작성하라고 한다.
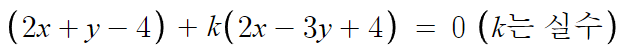
이 직선은 항상 2x+y-4=0 과 2x-3y+4=0 의 교점을 지난다.
두 직선의 교점을 지나며
또다른 점 (4, -1)을 지나는 직선은 하나밖에 없을것이므로
(4, -1)을 지나도록 하는 k값을 정해줘야한다.
따라서 (4, -1)을 위 식에 대입한다.
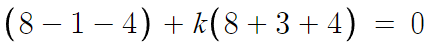
따라서 k = -1/5 이다.
이를 대입하면 직선의 방정식 작성이 완료된다.
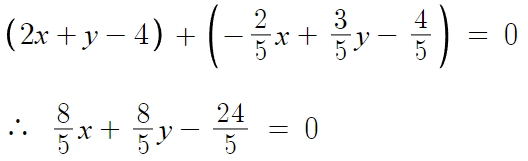
근데 문제에서는
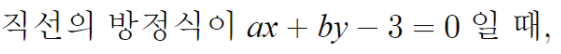
상수항이 -3 이라 하니까
그냥 방금 작성한 식에서 상수항이 -3이 되도록 변형만 해주면 된다.
양변에 5/8을 곱해주면 상수항이 -3이 된다.
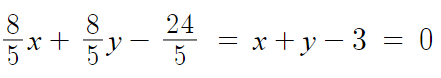
따라서 a=1, b=1 이고 2a+b = 3
따라서 답은 3
2 )
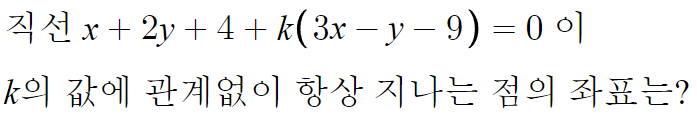
k의 값에 관계없이 항상지나는 점이 있다 =
그 점의 좌표를 대입하면 k의 값에 관계없이 항상 성립한다 =
k에 대한 항등식이다.
따라서 (x+2y+4)=0 과 (3x-y-9)=0 을 동시에 만족시키는 점을 구하면
그곳이 답이다.
x+2y+4=0 과 3x-y-9=0 을 연립하면 구할수 있다.
연립과정은 생략한다. x=2, y=-3 이다.
따라서 답은 (2, -3)
'수학(상) > IV. 도형의 방정식' 카테고리의 다른 글
| 원의 방정식 #1 - 원의 방정식의 작성 (0) | 2022.03.09 |
|---|---|
| 직선의 방정식 #5 - 점과 직선 사이의 거리 (0) | 2022.03.06 |
| 직선의 방정식 #3 - 두 직선의 평행과 수직 (0) | 2022.03.04 |
| 직선의 방정식 #2 - 직선의 방정식의 일반형 (0) | 2022.03.02 |
| 직선의 방정식 #1 - 직선의 방정식 작성 (0) | 2022.03.01 |



