
- 개요 -
말 그대로 어떤 원에 접하는 직선이 있을텐데
그 직선의 방정식을 구하는법을 다룰것이다.
이거 진짜 어려운 내용이니까 한번에 정복할생각은 접어두자.
- 1 : 기울기가 주어진 원의 접선의 방정식 -

처음이니까 같이 풀어보자.
직선의 방정식을 작성하려면
알아야 하는 것이
1. 기울기+지나는점 1개
2. 지나는점 2개
둘중 하나만 알면 된다.
여기선 기울기를 줬으니 지나는점만 구하면 될것이다.
지나는 점은 어떻게 구하느냐?
우리가 구하는게 원의 접선의 방정식이니까
이 직선이 원과 한 번 만난다고 하면 된다.
직선과 원이 한번 만날 조건은? 즉 직선이 원에 접할 조건은?

d = 점과 직선 사이의 거리
r = 원의 반지름
따라서, 다음과 같은 결론을 얻는다.
점과 직선 사이의 거리 = 원의 반지름 이라는 관계식을 쓰면 된다.
점과 직선 사이의 거리를 구하려면
일단 직선의 방정식의 틀은 잡아놔야한다.
문제에서 기울기가 1이라 했으니
직선의 방정식은 y=x+a 형태일것이다.
a값만 구하면 되는거다.
그리고 이 a값은 d=r 이라는 관계식을 써서 알아내는것이다.
근데 점과 직선사이의 거리는
직선의 방정식이 일반형이어야한다.
따라서 표준형인 y=x+a를 일반형인 -x+y-a=0 으로 바꾸겠다.
-x+y-a=0 이라는 직선과
원의 중심인 (0, 0) 사이의 거리가
원의 반지름과 같고
따라서 d = r = √(2) 이다.
d는 점과 직선사이의 거리 공식 적용하면

따라서, |-a| = 2 이다.
따라서 a=2 또는 a=-2 이고
아까 구한 직선의 방정식인 -x+y-a=0 에 각각 대입하면
답은
-x+y-2=0 또는 -x+y+2=0 이다.
Q) 원래 직선의 방정식이 두개가 나오나요?
A) 그렇다. 항상 두개 나온다. 증명은 좀 뒤에 다룬다.
- 2 : 원 위의 점에서의 접선의 방정식 -

이것도 똑같다.
접선의 방정식을 구하라는건 직선의 방정식을 구하라는거고
직선의 방정식을 작성하려면
1. 기울기+지나는점 한개
2. 지나는점 두개
이것중 하나를 알면 된다.
지나는점 하나를 문제에서 줬기때문에
기울기를 구하던가, 지나는 다른 점을 구하던가 하면 되는데
기울기를 구하는게 더 쉽다. 따라서 기울기를 구하는 방향으로 간다.
쓰이는 핵심 논리는
'원의 접선은 반지름과 수직이다'
따라서 (반지름의 기울기) × (접선의 기울기) = -1 임을 이용하면 된다.
혹시 왜 수직인지 모르는 사람을 위해 좀 설명해주자면
우선 직선이 원에 접한다는건 d=r 이라는거고
d는 원의 중심에서 '접선을 향해 수직하게' 그은 선분의 길이니까
원의 접선은 무조건 반지름과 수직이다.
반지름의 기울기는 구하기 쉽다.

원의 중심인 (0, 0)과
주어진 점인 (2, -1) 를 잇는 선분의 기울기를 구하면 된다.
따라서 반지름의 기울기는 -1/2 이다.
그럼 우리가 구하고자 하는 접선의 기울기는
-1/2 × (접선의기울기) = -1 니까
접선의 기울기 = 2 이다.
기울기를 알았고, 지나는점을 알았으니
직선의 방정식을 작성할 수 있다.
기울기가 2이고 (2, -1)을 지나는 직선의 방정식을 작성하면

이걸 정리하면 답은
y = 2x-5
여기서는 주의할게, 접선의 방정식이 하나 나온다.
문제에서 원의 어떤 점을 지나는 직선인지 알려줬기 때문이다.
그 점에서 반지름과 수직인 직선은 하나밖에 없고
그래서 이 문제에서는 답이 하나 나온다.
아까 기울기 주는 문제에서는
접선이 원의 어떤 점을 지나는지 안알려줬기때문에
조건을 만족하게 접선이 지날 수 있는 점이 두개가 되고,
그래서 답이 두개가 된것이다.
지금까지 요약하자면,
기울기랑 지나는 점을 알면 접선의 방정식을 작성할 수 있다.
문제에서는 지나는 점과 기울기중 하나밖에 안주기 때문에
직선이 원과 접하려면 d=r 이어야함을 이용하여 부족한 하나를 구한다.
- 심화 1 : 한 원에서 기울기가 같은 접선은 두개이다 -
아까 왜 두개가 나오는지 증명해준다 했는데
여기서 다룰것이다.
사실 직접 원을 그려본다음 접선을 그어보면
두개가 나올수밖에 없다는게 느껴지긴 할텐데
이걸론 찝찝해서, 빈틈없는 엄밀한 증명을 원하는 사람을 위해 설명해주겠다.
일반화해버리면 증명이 완료된다.

원의 중심은 (a, b)이고, 반지름은 r이고, 접선의 기울기는 m이다.
이게 항상 성립한다는걸 증명하면,
원의 중심이 어디있든, 반지름의 길이가 어떻든, 접선의 기울기가 어떻든
즉 a, b, r, m의 값에 상관없이
항상 성립한다는거니까
한 원에 대해 기울기가 같은 접선은 두개라는 것이 증명 완료된다.
그냥 하던대로 하면 된다.
직접 해보는게 좋지만, 처음 공부하는사람이 하기 쉽지는 않으니
증명과정을 적어는 놓겠다.

- 3 : 원 밖의 한 점에서 원에 그은 접선의 방정식 -

사실 원의 방정식은 얘가 본체이다.
개인적으로 수학(상)에서 가장 어려운 내용이라 생각한다.
하지만 얘가 새로운 내용이 있는건 아니다. 심화내용이라는 뜻이다.
얘가 왜 어려운 거냐면,
보통 원의 어떤 점을 지나는지 알려주거나, 기울기가 얼마인지 알려주는데
이 문제는 아무것도 알려주지 않는다.
'원 밖에서' 접선을 긋는거기 때문이다.
푸는 idea는 아래 둘중 하나를 취향껏 채택하면 된다.
1. 접점의 좌표를 (x₁, y₁)라 두고 연립방정식을 푼다.
2. 접선의 기울기를 m이라 두고 하던대로 한다.
즉, 기울기랑 접점의 좌표 둘다 안줬으니까
일단 미지수로 두고 푼다음
그 값은 나중에 구하겠다는 논리이다.
하던대로 한다는건,
우리가 하던대로 관계식 d=r을 이용해서 미지수의 값을 구하라는 뜻이다.
첫번째 방법부터 해보자.
1. 접점의 좌표를 (x₁, y₁)라 두고 연립방정식을 푼다.
원 밖의 점 (0, 2)와 원 위의 점 (x₁, y₁) 을 지나는 직선의 방정식을 구하면 된다.
원 위의 점을 지나는 직선의 방정식은
반지름과 기울기가 수직임을 이용해서 구했었다.
반지름의 기울기는 y₁/x₁ 이며
따라서 접선의 기울기는 -x₁/y₁ 이다.
기울기가 -x₁/y₁ 인 직선의 방정식은

미지수가 3개나 되는데, 하나씩 풀면 된다.
a값은 저 식에 (x₁, y₁) 대입하면 바로 구할 수 있다.
(x₁, y₁)은 원 위의 점이기 때문에, 원의 방정식에 대입해도 성립해야한다.

따라서, 위 식에 (x₁, y₁) 대입해서 정리해보면
a=2/y₁ 이다.

미지수 하나 없앴고, 나머지를 처리하자.
미지수가 x₁, y₁ 으로 두개니까,
관계식을 두개 세우면 된다.
우선 원의 방정식에서 얻어지는 관계식 하나

나머지 하나는 직선의 방정식에서 얻는데,
아직 쓰지 않은 정보인
이 직선이 (0, 2)를 지난다는걸 이용하면 된다.

여기에 (0, 2)를 대입하면
2 = 2/y₁ 이다.
따라서 y₁=1 이고,
아까 세운 원의방정식 관계식에 대입하면
x₁=1 또는 x₁=-1 이다.
여기선 운이 좋게도 x=0이라서 x₁이 소거된거라
귀찮게 연립할 필요는 없었지만, 다른 문제에선 해야할수도 있다.
아무튼 이제 다 구했으니 대입해주면 끝이다.

따라서 답은 y=-x+2 , y=x+2
다음으로, 기울기를 미지수로 두는 방법이다.
2. 접선의 기울기를 m이라 두고 하던대로 한다.
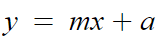
우선 a값을 바로 구할 수 있다.
문제에서 '이 직선이 (0, 2)를 지난다' 라고 했으니
대입해버리면 a와 m의 관계를 구할 수 있는것이다.
대입하면, a=2 이다.

이제 d=r 관계식을 쓰기 위해 일반형으로 정리하면

이제 d=r 관계식을 써주면


따라서 m = ±1 이고,
따라서 답은
y=-x+2 , y=x+2
Q) 얘도 접선이 두갠가요?
A) 그렇다. 이것도 증명해주겠다.
- 심화 2 : 원 밖의 점에서 한 원에 그은 접선은 두개이다 -
이것도 원이랑 원 밖에 점 찍어본다음 접선 그려보면
두개가 나올수밖에 없다는게 느껴질텐데
얘도 아까처럼 수식으로 엄밀하게 증명해주겠다.

고1까지의 수학만으로 증명이 가능하지만
이건 고1이 하기는 너무 어렵기때문에
처음 공부하는사람은
일단 접선이 두개구나 라고 받아들이고
나중에 실력이 늘었을 때 해보는걸 추천한다.
고1이라고 무시하는거냐면서 기분나빠할수 있는데
아마 증명과정을 보면 수긍할거다. 너무 어렵다.
- 예제 -
1 )

기울기가 -3인 직선의 방정식이므로
일단 y=-3x+a 형태이다.
a값만 구하면 된다.
접한다는건 d=r 이라는거고 이걸 이용한다고 했었다.
점과 직선사이의 거리공식을 쓰기 위해
y=-3x+a를 일반형으로 바꾸면
3x+y-a=0 이다.

따라서 a=-10, a=10 이며
각각 대입해주면, 답은
y=-3x-10, y=-3x+10
2 )

접선은 반지름과 수직이다.
반지름의 기울기는 -2 이므로
접선의 기울기는 1/2 이다.
따라서 접선의 방정식은

이런 형태이다.
이제 1번문제와 숫자만 바꾸고 그냥 똑같아졌으니 하던대로 해주면 된다.
d=r 관계식을 이용하기 위해 일반형으로 바꿔주면

이제 d=r 관계식을 써주면

따라서 a=±5 이다.
근데 a=-5는 될수 없다.
a=-5 라면

이렇게 돼야하는데, (-2, 4)를 대입해보면 성립하지 않음을 알 수 있다.
(-2, 4)는 저 직선 위에 있지 않은것이다.
따라서 a=5이다.
따라서 답은

3 )

핵심 : 기울기, 접점 둘다 모르니
그냥 미지수로 두고 식을 세운다음 값은 나중에 찾는다.
난 개인적으로 기울기를 미지수로 두는게 편하다
미지수가 하나 줄어들기 때문이다.
물론 취향이니까 접점을 미지수로 두고 풀어도 전혀 틀린 풀이가 아니다.
아무튼 기울기를 m이라 두면
y = mx+a
(2, 5)를 대입하면 a = 5-2m
따라서 y = mx-2m+5
d=r 관계식을 쓰기 위해 일반형으로 바꾸면
-mx+y+2m-5 = 0
이제 d=r 관계식을 써주면

m에 대한 이차방정식을 구했다.
근과 계수의 관계에 의해
m의 값의 곱은 -1이다.
따라서 답은 -1
4 )

증명하라해서 어려워보이지만 쉬운문제다.
그냥 접선의 방정식을 구하면 되는거다.

'수학(상) > IV. 도형의 방정식' 카테고리의 다른 글
| 점과 도형의 대칭이동 (0) | 2022.03.30 |
|---|---|
| 점과 도형의 평행이동 (0) | 2022.03.26 |
| 원의 방정식 #3 - 원과 직선의 위치관계 (0) | 2022.03.16 |
| 원의 방정식 #2 - 두 원의 교점을 지나는 원과 직선의 방정식 (0) | 2022.03.11 |
| 원의 방정식 #1 - 원의 방정식의 작성 (0) | 2022.03.09 |





