
- 개요 -
수학(상)의 마지막 내용이다.
여기는 너무 당연한걸 설명하려니 딱히 설명할게 없어서
좀 설명이 빈약한 느낌이 있는데,
어차피 여기는 문제풀면서 감 잡는 단원이다.
- 대칭이동이란? -
말 그대로 대칭하게 이동하는것
정확히는, 주어진 점 또는 직선에 대하여 대칭인 도형으로 옮기는 것
을 대칭이동이라 한다.
1. x축에 대한 대칭이동,
2. y축에 대한 대칭이동
3. 원점에 대한 대칭이동
4. y=x에 대한 대칭이동
이거 4개만 할 줄 알면 나머지는 여기서 응용할수 있다.
우선 점을 대칭이동한다음, 다음으로 도형의 대칭이동을 다룰것이다.
- 대칭이동 1: x축에 대한 대칭이동 -
점 (2, -3)을 x축에 대하여 대칭이동한 점의 좌표는?
x축에 대하여 대칭이동하면 어떻게 되는지를 그림으로 보자.
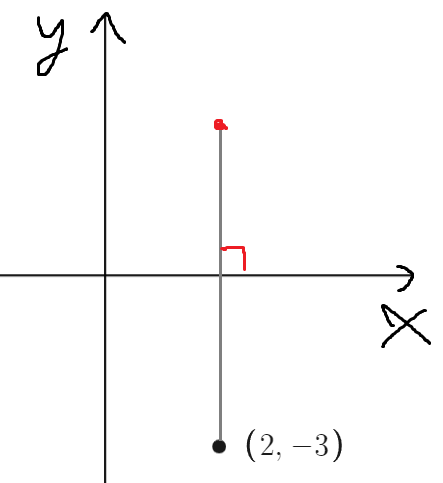
x축에 대하여 대칭이동하라는건
x축을 기준으로 접어버리라는거다.
데칼코마니를 떠올려보면 쉽다.
그럼 접혀서 나오는 점의 좌표는?
x축을 기준으로 접었으니 x좌표는 변하지 않고
y좌표만 변할것이다.
그리고 x축을 기준으로 '대칭'이므로 -3에서 3으로 변할것이다.
따라서 대칭이동한 점의 좌표는 (2, 3) 이다.
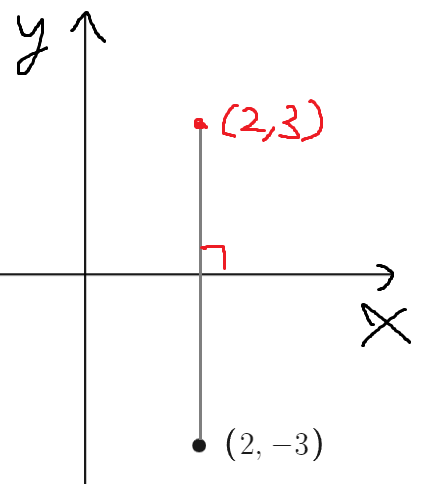
일반화해보자.
점 (a, b)를 x축에 대하여 대칭이동한 점의 좌표는?
x축을 기준으로 접어버리는거니까
x좌표는 변하지 않고, y좌표만 부호가 반대가 된다.
따라서 (a, b)를 x축에 대하여 대칭이동한 점의 좌표는 (a, -b) 이다.
요약 : x축에 대한 대칭이동은, y좌표의 부호만 바뀐다.
- 대칭이동 2 : y축에 대한 대칭이동 -

그냥 똑같다.
이번엔 y축을 기준으로 접었으니
y좌표는 그대로고, x좌표의 부호만 바뀔것이다.
바로 일반화하면,
(a, b)를 y축에 대해 대칭이동하면
(-a, b)
요약 : y축에 대한 대칭이동은, x좌표의 부호만 바뀐다.
- 대칭이동 3 : 원점에 대한 대칭이동 -

이건 조금 다르다.
'점'에 대한 대칭이동이기 때문에
이건 하던대로 '한번 접기'로 이해할수 없다.
그럼 어떻게 하느냐?
두번 접으면 된다.
무슨 말이냐?
저 그림만 봐도, 대칭이동된 점의 좌표는
딱봐도 x좌표 -2이고 y좌표 3아닌가?
x좌표와 y좌표의 부호가 둘다 바뀐다는거다.
그러려면, x축을 기준으로도 접고 y축을 기준으로도 접으면 되는거다.

따라서 대칭이동된 점의 좌표는 (-2, 3)이다.
조금 심화로 자세히 설명해주자면,
대칭이동하기 전의 점과, 대칭이동한 후의 점의 평균지점이
바로 원점이다.
이 논리는 꼭 알아야한다.
원점이 아니라 (1, 2)를 기준으로 대칭이동하면 어떡할건가?
원점은 (0, 0)이고
대칭이동하기 전의 점이 (2, -3)인데
대칭이동 후의 점과 점(2, -3)을 평균내면
(0, 0)이 나올거라는 뜻이다.
따라서, 대칭이동 후의 점의 좌표는 (-2, 3)이다.
그럼 바로 심화해볼까?
점 (2, -3)을 점 (1, 2)를 기준으로 대칭이동한 점의 좌표는?
대칭이동된 점의 좌표를 P(x, y)라고 하자.
그러면 x좌표의 평균인 (2+x)/2 = 1 이고
y좌표의 평균인 (-3+y)/2 = 2 이다.
따라서 x=0이고, y=7이다.
따라서 답은 (0, 7) 이다.
이것도 두번접기로 이해할 수 있다.
대신 x=1과 y=2를 기준으로 접어야하며,
이러면 단순히 부호만 바꿔서 되는게 아니라,
x=1, y=2와 점이 얼마나 떨어져 있었는지를 보고 맞는 수치를 넣어줘야한다.
왜냐면, x축대칭할때 그냥 부호바꿔서 풀었던 이유는
x축이라는건 y=0 이라서
대칭이동된 점의 좌표를 구하고싶다면
그냥 부호만 바꿔주면 평균이 0이 나오기 때문이다.
- 대칭이동 4 : y=x에 대한 대칭이동 -
점 (2, -3)을 y=x에 대해 대칭이동한 점의 좌표는?
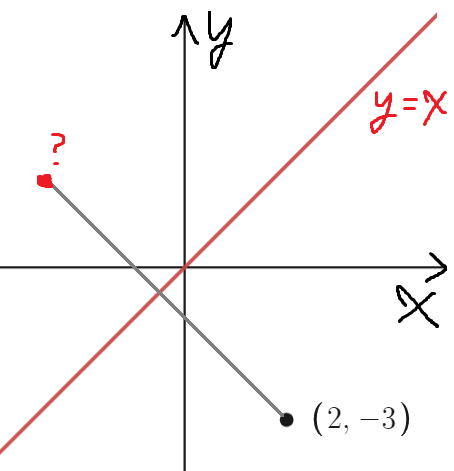
이건 조금 어렵다.
y=x를 기준으로 접어버린 점이 결과긴 하지만
y=x를 기준으로 접는걸 어떻게 다뤄야할지 바로 보이지 않는다.
이럴때, 내가 아까 알려준 심화 논리를 써야한다.
'대칭이동되기 전과 후의 점의 평균지점이 바로 대칭이동의 기준점이다.
따라서 대칭이동되기 전과 후의 점의 평균지점이 y=x 위에 있다.'
대칭이동된 후의 점을 P(a, b)로 한다음 구해보겠다.
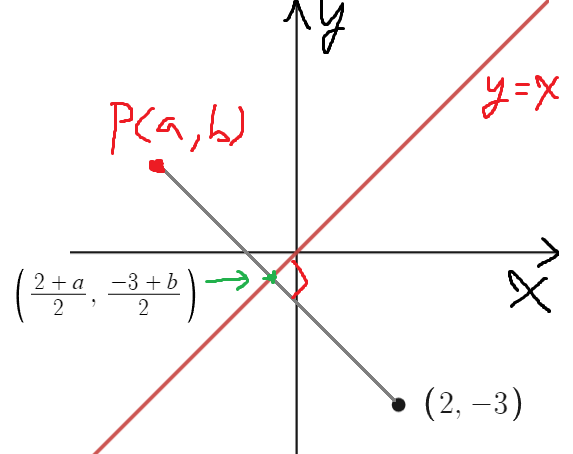
그러면 평균지점은 x = (2+a)/2 , y = (-3+b)/2 이고
이 점이 직선 y=x 위에 있으니까
그대로 대입해주면 된다.
(-3+b)/2 = (2+a)/2
따라서 b=a+5 이다.
이제 a값만 구하면 되는데,
아직 쓰지 않은 조건이 있다.

그건바로
대칭이동 전후의 점을 이은 선은
y=x와 수직이라는것
따라서 대칭이동 전후의 점을 이은 선의 기울기는 -1이다.
근데 기울기 = y변화량/x변화량 이므로
아래 식이 성립한다.

따라서 a=-3 이다.
따라서 b=2 이다.
따라서 대칭이동된 점의 좌표는 (-3, 2)이다.
근데 신기한걸 발견했다.
대칭이동하기 전의 점이 (2, -3)인데
y=x에 대해 대칭이동시켰더니
x와 y를 바꾼 (-3, 2)가 됐다.
실제로 그렇다.
y=x에 대해 대칭이동한 것의 좌표를 구하고싶으면
x와 y좌표를 서로 바꿔주면 된다.
따라서 일반화하자면,
점 P(a, b)를 직선 y=x에 대해 대칭이동한 점의 좌표는
x와 y를 바꿔서 P'(b, a)이다.

바로 증명해주겠다.

- 도형의 대칭이동 -
y=f(x)를 x축에 대하여 대칭이동해보자.
대칭이동된 점의 좌표를 (x', y') 이라 하면
x' = x
y' = -y 이다.
따라서 x = x', y = -y' 이고,
이를 대입하면
-y' = f(x')
x', y'은 임시로 추가한 미지수인데
그냥 x와 y라는 뜻이니까 ' 떼버리면
-y = f(x)
즉 점의 대칭이동과 똑같다.
y축에 대하여 대칭이동하는것과
원점에 대하여 대칭이동하는것도
완전히 똑같이 할수있으니 생략
결론만 알려주자면
y축에 대하여 대칭이동하면
x대신 -x넣으면 된다. y = f(-x)
원점에 대하여 대칭이동하면
y대신 -y, x대신 -x 넣으면 된다. -y = f(-x)
다음으로 조금 어려울수 있는게
y=x에 대한 대칭이동인데,
이것도 쉽다.
x' = y
y' = x
따라서 y=f(x)에 대입해주면
x' = f(y') 이고
' 떼주면
x = f(y)
Q) 도형의 평행이동은 비중을 많이 두고 다루던데, 여기서는 왜 대충하나요?
A) 도형의 대칭이동은 점의 대칭이동과 사실상 똑같은거라 더 설명할게 없다.
어차피 똑같은거니 점의 대칭이동을 이용해 도형의 대칭이동을 다루는법을
적당히 귀띔해주고 넘어가는것이다. 문제를 풀어보면 무슨 말인지 안다.
- 예제 -
1 )

x축에 대해서 대칭이동하면 y좌표의 부호만 바뀐다.
따라서 답은 (3, -2)
2 )

이거 풀수 있다면
점의 대칭이동은 이해했다고 보면 된다.
우선 점 A가 y=x+2 위에 있으므로
점 A의 좌표를 (a, a+2)로 표현할 수 있다.
그러면 B의 좌표는
A를 y=x에 대해 대칭이동한 점이니까
B의 좌표는 x랑 y 바꾸면, (a+2, a) 이다.
그리고 C는 또 B를 원점에 대하여 대칭이동한거라 한다.
따라서 C의 좌표는 x랑 y 부호 바꾸면, (-a-2, -a) 이다.
근데 (-a-2, -a) = (-4, -2) 이므로
a=2 이다.
따라서 점 A의 좌표는 (2, 4)이다.
따라서 답은 (2, 4)
3 )

원점에 대하여 대칭이동했으므로
x자리에 -x, y자리에 -y 넣으면 된다.
그러면 -x+4y-5=0 이 되고
이게 답이다.
따라서 답은 -x+4y+5=0
4 )
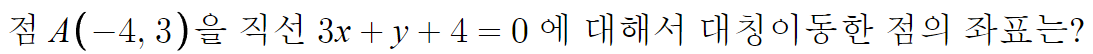
y=x에 대한 대칭이동 의 심화내용이다.
쓰이는 논리는 똑같다.
대칭이동한 점을 B라 하면,
A와 B의 중점은 직선 3x+y+4=0 에 있다.
B의 좌표를 (a, b)라 하고 중점을 M이라 하겠다.
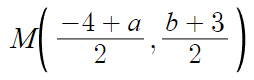
이 중점 M이 직선 3x+y+4=0 위에 있다.
따라서 대입해주면
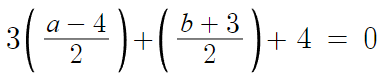
이를 정리하면 b를 a에 대해 나타낼 수 있다.

이걸 대입해서 M의 좌표를 다시쓰면
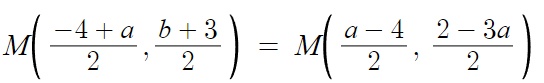
이제 a만 구하면 되는데,
아직 안 쓴 정보가 있다.
선분 AB가 직선 3x+y+4=0과 수직하다는 정보이다.
3x+y+4=0 의 기울기는 -3 이므로
선분 AB의 기울기는 1/3 이다.
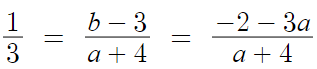
이를 정리하면, a=-1 이고
따라서 b=4
따라서 답은 (-1, 4)
수학(상) 끝
'수학(상) > IV. 도형의 방정식' 카테고리의 다른 글
| 점과 도형의 평행이동 (0) | 2022.03.26 |
|---|---|
| 원의 방정식 #4 - 원의 접선의 방정식 (0) | 2022.03.20 |
| 원의 방정식 #3 - 원과 직선의 위치관계 (0) | 2022.03.16 |
| 원의 방정식 #2 - 두 원의 교점을 지나는 원과 직선의 방정식 (0) | 2022.03.11 |
| 원의 방정식 #1 - 원의 방정식의 작성 (0) | 2022.03.09 |



