
- 개요 -
유리함수를 다루기 전에,
당연히 유리식이 뭔지부터 알아야하고,
이를 다룰 줄도 알아야한다.
유리식에 대해, 이 한 글에 전부 담은거라서
내용은 조금 많다.
그리고, '함수'는 상당히 중요하고 내가 개인적으로 좋아하는 단원이기 때문에
이 단원에서 내가 제시하는 예제문제는
대부분 본인이 중요하다고 생각되는 부분을 찝어낸 자작문제이다.
이건 자신있으니 믿고 따라오면 된다.
이것들을 풀 줄 알아야 다음 진도를 무난하게 진행할 수 있다.
- 유리식이란? -

쉽게 말해서,
두 다항식의 나눗셈 꼴로 나타내지는 식은 다 유리식이다.
유리수와 비슷한 느낌이지 않은가?
그 느낌이 맞다. 그래서 이름이 유리식인것이다.
두 정수의 나눗셈 꼴로 나타내지는 식이 유리수이고
두 다항식의 나눗셈 꼴로 나타내지는 식이 유리식이다.
예를 들어주겠다.
아래는 전부 유리식이다.
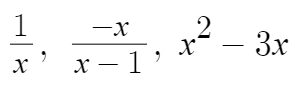
다항식도 유리식이다.
분모가 1인 유리식인것이다.
- 유리식을 다루는 방법 : 핵심 -
1 : '유리식'은 '비율'이다.
2 : '유리수'를 다룰때와 똑같이 다룬다.
유리수를 다룸에 있어서,
이 두가지에서 벗어나는 상황은 아무것도 없다.
이 두 문장의 의미를 차례차례 곱씹어보면서
유리식을 다루는 방법을 정복할것이다.
이게 현재 수학 교재들에는
정말 불친절하게 공식만 설명되어있는데,
위의 두 문장(핵심)만 이해하면 모든 곳에 응용이 가능하며,
이렇게 공부하는게 더 쉽다.
이렇게 공부하면 '공식'을 외울 필요가 하나도 없어진다.
'원리' 자체를 이해하게 되는것이기 때문이다.
- 1 : 유리식은 비율이다 -
무슨 말이냐면,

다항식 A를 다항식 B로 나눈 식이 바로 유리식인데,
수학을 이쯤 했으면 수상하게 느꼈을만한게 있다.
왜 사칙연산 식에서 곱셈, 나눗셈기호인 ×, ÷ 는 잘 나타나지 않는것인가?
곱셈, 나눗셈을 표현하는 더 직관적인 방법이 있기때문이다.
그중 곱셈기호는 보통 A×B 대신 AB 로 표현하여 생략하고,
나눗셈을 표현하는 직관적인 방법은 바로,
분수로 나타내는것이다.
A÷B 대신 A/B 로 표현하는것이다.
즉,
유리식은 분수식이다.
근데 분수는 비율이다.
따라서, '유리식'은 '비율'이다.
초등학생때 '비례' 배웠을것이다.
비례는 두 수의 비율관계를 나타내는 식이다.
비례의 다른표현이 바로 '분수'이다.

따라서, 우리가 배웠던
'비례' 다루는 방법을 그대로 가져오면 된다.
'비례'의 성질을 가져오자.
a : b = 1 : 2 라는 비례식이 있다고 해보자.
그럼 a와 b의 비율이 1:2 라는것이고
이는 b가 a의 2배 라는 뜻이다.
근데, a와 b의 비율만 알지
a와 b의 정확한 값은 모른다.
그래서 이걸 이렇게 표현한다.
a = k 라 두면,
b는 a의 2배이므로
b = 2k 이다.
따라서,
a : b = k : 2k 이다.
(단, k는 0이 아닌 실수)
a는 1에 어떤 수 k가 곱해져서
b는 2에 어떤 수 k가 곱해져서
만들어진 수라고 보는것이다.
k가 0이 아닌 실수라는건 뭔말이냐면,
k=0 이면 비례식 자체가 성립하지 않으니 제외한것이다.
그리고, 이 k값은 a:b = 1:2 인것만 가지고는 모른다.
아무튼 k를 둘다 똑같이 곱해주기만 하면
a와 b의 비율관계 자체에는 아무런 영향을 주지 못하므로,
이렇게 표현해도 아무 문제가 없다.
아니, 이렇게 표현하는게 다루기 더 쉽다.
왜 이게 더 쉬운지는 보다보면 안다.
그리고 이 k값은 문제에서 따로 주는 단서로 알아내는것이다.

무슨 말인지는 문제 하나만 풀어보면 바로 감을 잡는다.

a : b = 2 : 3 이므로,
a = 2k 라 두면 b = 3k 가 된다.
따라서,

답은 1이다.
- 중간점검 예제 -
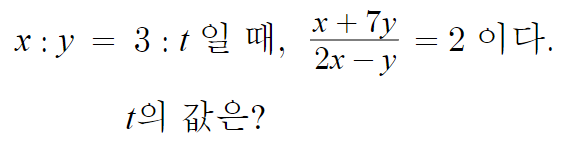
x : y = 3 : t 이므로,
x = 3k 라 두면, y = tk 이다.
따라서,

따라서 답은 1이다.
- 2 : 유리수를 다룰때와 똑같이 다룬다 -
그래서 이 성질을 구체적으로 어떻게 써먹느냐?
유리식끼리 계산할 때 쓴다.
유리식은 비율이고,
비율은 분수이므로
분수의 성질은 곧 유리식의 성질이다.
그리고 유리식은 유리수와 똑같이 다루므로,
그냥 우리가 여태 분수 계산하던대로 하면 된다.
예를 들어서, 이런 복잡한 '유리식'을 약분하고싶다.

이걸 약분할때 쓰이는 재료가 바로 분수의 성질이다.
분수는 곧 분자와 분모의 비율이므로,
분자와 분모에 같은 수를 곱하거나, 나눠도
분수의 값은 변하지 않는다.
분모 분자에 같은 수를 곱해도 비율은 변하지 않는다.
그니까 그냥 우리가 하던대로 하면 된다.

분모, 분자엔 둘다 4xy가 곱해져 있고
4xy를 분모 분자에 똑같이 나눠줘도 비율은 변하지 않기때문에
분수의 값 또한 변하지 않는다.
주의할 것은, 0으로 나누는 연산은 불가능하기때문에
분모 분자에 0을 곱해서 계산하는 황당한 실수는 하지 말자.
하나 더 해볼까?

하던대로 한다.
통분 = 분모를 같게 만드는것.
따라서 분모를 둘다 BD로 만든다.
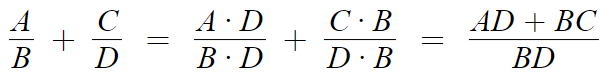
조금 설명을 덧붙여주자면,

그냥 하던대로 하는거라서,
하나도 안어렵다.
- 중간점검 예제 -

- 첫번째 식 -
하던대로 계산한다.
'유리식의 덧셈' 이다.
'분수의 덧셈' 과 똑같이 푼다.
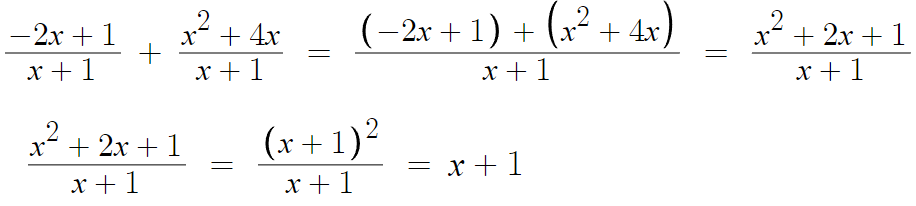
따라서 첫번째 식의 답은 x+1
- 두번째 식 -
하던대로 계산한다.
'유리식의 사칙연산' 이다.
'분수의 사칙연산' 과 똑같이 푼다.

따라서 두번째 식의 답은
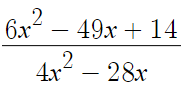
- 특수한 형태의 유리식 1 : 번분수 -
번분수 : 분모나 분자에 또 다른 분수가 있는 것
이건 예를 들어주는게 이해가 빠르다.

이런게 바로 번분수이다.
말그대로 번잡한 분수인것이다.
그래서 이걸 '번잡하지 않게' 만드는게 목적이다.
보다시피 저대로는 풀기 머리아프다.
문자 4개가 위아래로 쭉 늘어서있다니.
이걸 푸는 방법은 간단하다.
분수 안에 분수가 또들어가서 너무 번잡하니까
이 번잡함을 없애주면 되는거다.
분모의 C/D 에서 D를 없애고
분자의 A/B 에서 B를 없애면 될것이다.
그리고 그 방법으로, '분수의 성질' 을 이용한다.
분모, 분자에 같은것을 곱해도 분수의 값은 변하지 않는다.
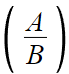
이게 분모고, B를 없앨것이다.
그럼 B를 곱하면 된다.
분모 분자에 똑같이 B를 곱해주면
분수의 값이 변하지 않을것이다.

이러면 분자에서 걸리적거리는 B를 없앴다.
이제 분모에서도 D를 없앨 차례다.
똑같이 한다. 분모 분자에 D를 곱한다.

번분수를 우리가 많이보던 '익숙한' 형태의 분수로 바꿨다.
이 방법을 이용하면 분수가 몇개 겹쳐있든
이런 익숙한 형태의 분수로 바꿀 수 있다.
근데 좀 세련되게 가자.
번분수를 한번에 익숙한 형태의 분수로 바꾸자.
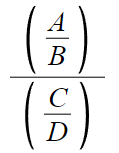
우리의 목적은, 여기서 B와 D를 없애는거다.
그러면, B와 D를 둘다 곱하면 된다.
아까는 처음하는거니까 그 과정을 하나하나 해준거다.
이젠 한번에 가자.
B와 D를 둘다 없앨거니까
분모 분자에 BD를 곱하는거다.

난 수학학원에서 이걸 처음 배울때,
암기를 도와주겠다며
'중'간에 있는것들끼리 곱해서 분'모'로,
'위아래'에 있는것들끼리 곱해서 분'자'로 넣는다 해서
중중모 상하자 로 외웠었다.

그냥 참고만 하자.
어차피 분모분자에 BD 곱하면 저거랑 완벽히 똑같은 결론이 나온다.
그리고, 꼭 분모 분자에 분수가 하나씩만 오라는법은 당연히 없다.

이런것도 번분수이다.
생긴건 무시무시해도 별거없다.
그냥 똑같이 풀면된다. 대신 여러번해줘야돼서 귀찮다.
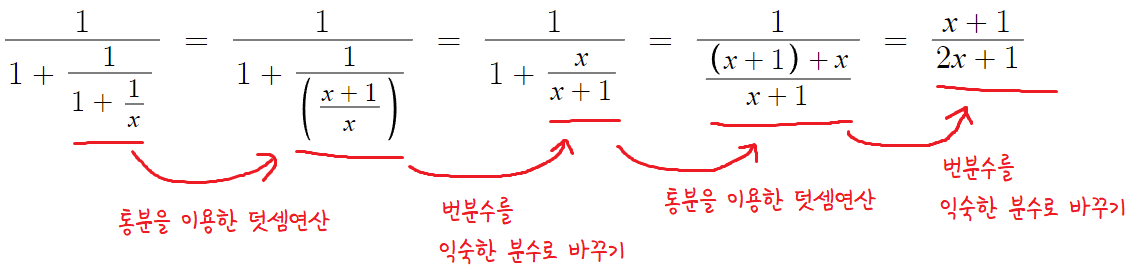
정수와 분수의 덧셈을 하기 위해, 통분한다.
그렇게 덧셈계산된 번분수를 익숙한 분수로 바꾼다.
그 과정을 반복한다.
- 특수한 형태의 유리식 2 : 부분분수 -
이번에 하는것중 가장 어려운 내용이다.
결론부터 말하자면,
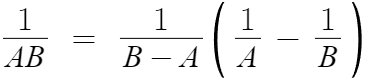
식만 더 길어지고 이게 뭐하는건가 싶겠지만,
A와 B의 곱꼴로 나타내어진 식을
A와 B를 쪼개서 다시 쓴다는 것에 의미가 있다.
즉, 통분되어있는 식의 분모를 다시 쪼개는것이다.
주로 복잡한 유리식들끼리 계속해서 더하고 뺄때 쓰인다.
저렇게 쪼개서 만들어진 우변을 '부분분수'라 한다.
예를 들어, A = 2x 이고 B = 2x+1 이라 해보자.

B - A = 1 이기때문에,
쪼개면 식이 오히려 간단해진다.

그래서 어떻게 나온식인지 같이 증명해보자.
증명할때도 '유리식의 성질' 이 이용된다.
즉 '분수의 성질' 을 이용한다.

분모, 분자에 같은것을 곱해도
분수의 값은 변하지 않는다.
분모 분자에 (B-A) 를 곱하면 바로 증명된다.

구체적으로 어떻게 쓰이는지는,
예시문제를 하나 같이 풀어주면서 보여주겠다.

분모에 있는 인수들을 보면
서로 빼면 전부 상수항만 남는다.
(x+1) - (x) = 1 , (x+2) - (x+1) = 1 , (x+5) - (x+2) = 3
이런 특별한 규칙이 반복되어 분모로 들어갔으니,
부분분수로 바꿔보면 어떨까 하고 추론해볼 수 있다.

따라서 답은

근데, 꼭 두 분수의 차 꼴로밖에 못쪼개나?
당연히 두 분수의 합 꼴로도 쪼갤 수 있다.
다만, 이런건 잘 쓰이지는 않는다.
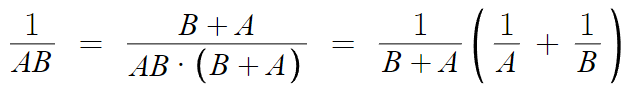
- 예제 -
아까도 말했지만,
일부러 조금 어렵게 냈다.
1 )

유리수의 사칙연산을 활용한 방정식 문제이다.
우선 너무 복잡하니 식을 간단히 할 필요가 있다.
분수끼리 더하는것이므로, 통분하여 계산한다.
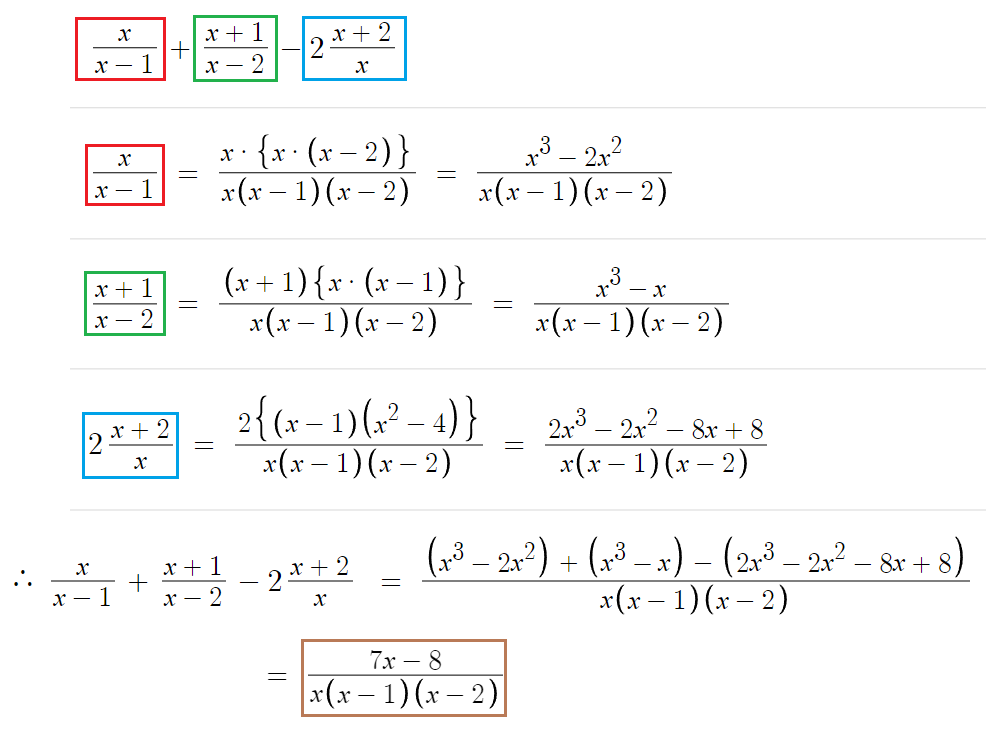
과정이 조금 더러운데, 유리식은 원래 좀 더럽다.
그럼 좌변을 구했으니
이제 좌변 = 우변 을 만족하는 실수 x만 찾으면
그게 바로 방정식의 근이다.
좌변은
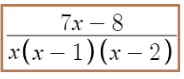
우변은
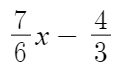
따라서, 우리가 구하고자 하는 방정식은
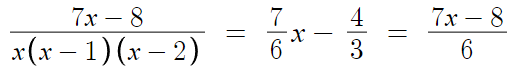
이걸 풀면 된다.
좌변과 우변이 둘다 7x-8 을 인수로 가지므로
7x-8 = 0 이면 좌변과 우변이 둘다 0이 되면서 방정식을 만족할거고,
그렇지 않으면 7x-8 을 약분해버리고
그러면 분자가 둘다 1이 된다.
분자가 둘다 1이됐으니 분모가 서로 같다고 두면 될것이다.
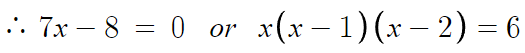
왼쪽의 일차방정식부터 풀어보면,
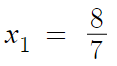
다음으로, 오른쪽의 삼차방정식을 풀어보자.
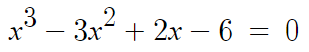
인수정리를 이용하기 위해,
x에 하나씩 대입해본다.
하나씩 대입하다보면, x=3 에서 0이 됨을 알 수 있다.
따라서, 두번째 실근은 x=3 이며,
저 식은 x-3 을 인수로 갖는다.
그럼 나머지 인수는?
조립제법을 이용하면 된다.
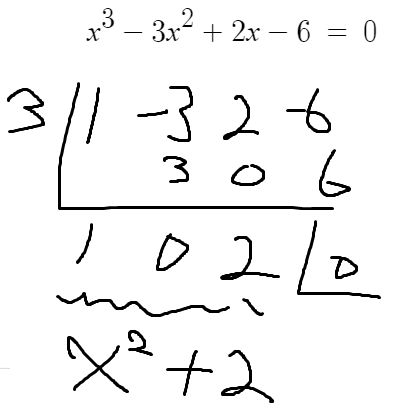
따라서, 이걸로 인수분해를 마무리할 수 있다.
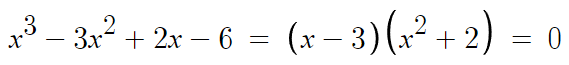
x²+2 = 0 의 실근은 없으므로,
실근은 아까 구했던 두개 뿐이다.
둘을 더해주면 끝
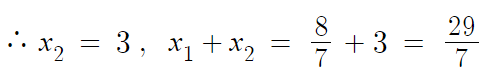
따라서 답은 29/7 이다.
2 )

사실 두 문제를 하나로 합쳐놓은 문제이다.
a값부터 구하고, 아래의 방정식을 해결하는게 당연한 절차이다.
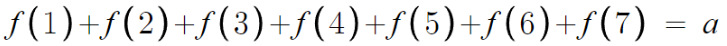
이것부터 해결하자.
근데, 인간적으로 함숫값 7개 전부 구한다음 다 더하라는걸까?
대부분은 그렇지 않다.
함숫값을 구하게하는것이 문제의 목적이면, 굳이 7개씩이나 더하게 만들 이유가 없다.
무슨 말이냐면, 저 함숫값들을 정말 하나씩 다 구해서 더하라는게 아니라,
저 함숫값 사이의 관계를 찾아내서 계산을 간단히 만들라는거다.
이건 문제의 출제의도를 파악하는 엄청난 팁이니 꼭 알아두자.
물론, 하나씩 전부 구해도 된다.
근데 아마 엄청나게 오래걸릴거다.
그리고 여기선 7개 더하라했지만,
만약 100개를 더하라는 문제가 나오면?
그럼 100개를 다 구할건가?
당연히 뭔가 규칙이 있겠구나 라는 생각으로 접근하는것이다.
하나씩 다 구해서 더하러면 아마 한시간은 걸릴거다.
즉, f(x)에 어떤 특성이 있기때문에
저렇게 황당하게 길어보이는 계산을 시킬수 있는것이다.
예를 들면, 1+2+3+4-3-2-1 = 4 가 되는것처럼
뭔가 규칙이 있어서 계산이 간단해질것이니
그걸 찾아보는 방향으로 풀어보라는 말이다.
물론 항상 그런건 아니므로,
정말 하나씩 함숫값을 구하는 방법도 염두에 두긴 해야한다.
어쨌든, f(x)에 뭔가 특성이 있으니까 저렇게 출제한것 아닐까?
f(x)를 분석해보자.
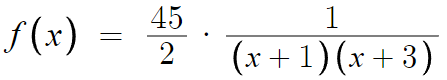
상수를 밖으로 빼내고 나니 뭔가 수상하지 않은가?
분모가 두 다항식의 곱인데,
두 다항식을 서로 빼면 2가 나온다.
(n+3) - (n+1) = 2 이기 때문이다.
게다가, 이런 분수를 계속 더하라한다.
따라서, '이거 부분분수로 분해하면 될거같다.'
라고 추론해볼 수 있다.
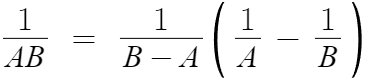
이 식을 이용하면 어렵지 않게 분해된다.
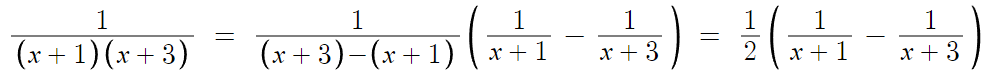
이제 이걸 대입해보면,
내가 왜 이것의 함숫값을 7번이나 더하게 시켰는지 눈치챌것이다.
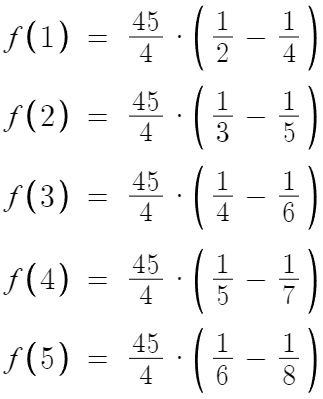
이걸 f(7)까지 한다음 전부 더한걸 구할건데,
보면 알겠지만, 전부 더할필요 없이 다 소거된다.
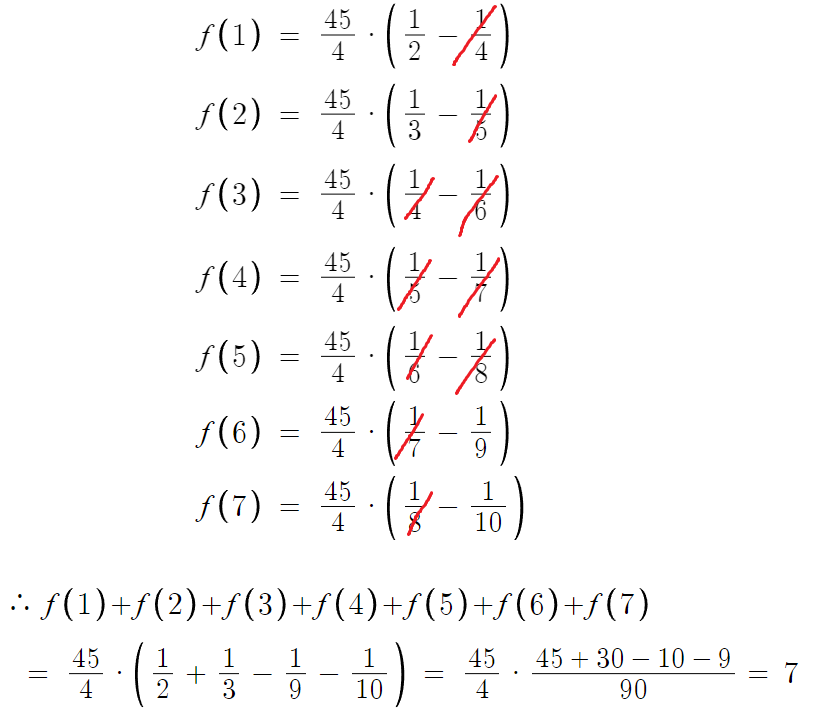
따라서, a=7 이다.

이제 이것만 풀면 된다.
a=7 을 대입해서 식을 다시쓰면
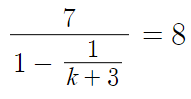
보면 알겠지만, 번분수라서 답이 바로 보이지 않는다.
번분수는 우리 눈에 익숙한 분수로 바꿔줘야한다.
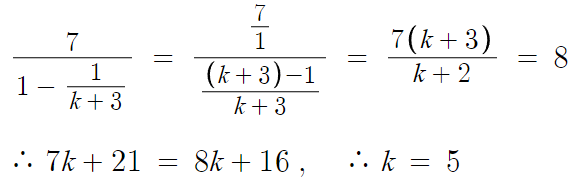
첫번째 변환이 이해가 안될수 있는데,
7은 분모가 1인 분수로 쓸수있다. 7 = 7/1 이다.
아무튼 답은 5
'수학(하) > II. 함수' 카테고리의 다른 글
| 함수 #6 - 합성함수 (0) | 2022.07.10 |
|---|---|
| 함수 #5 - 무리함수 (0) | 2022.07.07 |
| 함수 #4 - 유리함수 (0) | 2022.07.04 |
| 함수 #2 - 기본적인 여러가지 함수와 함수의 그래프 (0) | 2022.06.04 |
| 함수 #1 - 함수란 무엇인가? (0) | 2022.06.01 |



