- 등속직선운동과 이동거리 -
어떤 물체가 일정 한 속도로 직선 운동한다고 해보자.
이때 물체는 등속직선운동 한다고 하고,
속도, 시간, 이동거리(변위)와의 관계는이동거리 : s, 속도 : v, 시간 : t라 하면 s = vt이다.

0초부터 t초까지 v의 속도로 움직였으므로
아까와 같이 이동거리는 s=vt로 구할 수 있다.
직사각형의 넓이는 가로 x 세로 이다.
s=vt이고 그래프에서 가로는 t, 세로는 v이므로
이동거리 s는 가로 t, 세로 v인 직사각형의 넓이 vt와 같다.
직사각형의 넓이 = 속도 v를 시간 t에 대하여 적분한 값
- 가속도 -
가속도란 시간에 따라 물체의 속도가 변하는 정도를 나타내는 물리량이다.
즉 단위시간(1초)동안의 속도 변화량
가속도는 보통 a(acceleration)라고 쓴다.
가속도 : a = 속도 변화량 / 걸린 시간 = ( 나중속도 - 처음속도 ) / 걸린 시간
처음속도를 v0, 나중속도를 v라고 하면

가속도는 '속도'의 변화량을 나타내는 물리량이다.
속도는 크기와 방향을 갖고있는 벡터값이다.
따라서 위의 식으로 계산하면 가속도도 벡터값이 나온다.
쉽게 말해서 가속도도 방향을 갖는다.
예를 들어 물체를 동쪽 방향으로 밀어서 운동시키면
가속도의 방향은 동쪽 방향이 되는것이다.
- 등가속도 운동 -
등가속도 운동은 말 그대로 가속도가 같은 운동이다.
당연하지만 가속도가 같다는것은 가속도의 크기와 방향이 같다는 뜻이다.
등가속도 직선운동의 속도-시간 그래프를 그려보면


위 식을 v만 남기고 정리하면

이때의 이동거리 s는 속도를 시간에 대해 적분하여 구할 수 있다.

따라서 이동거리 s는 속도 v를 시간 t에 대하여 t=0부터 t=t까지 적분하여 구하고
이 결과값은

여기서

를 t에 대한 식으로 바꾸면


에 대입하여 정리하면
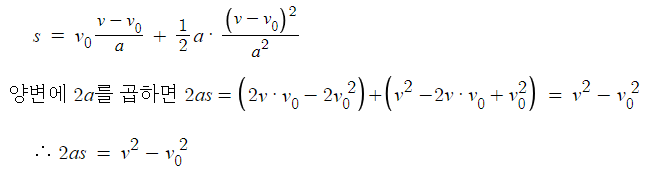
- 등가속도 운동 요약 -
가속도가 일정한 운동이다.



- 등가속도 운동에서의 평균 속도 -
방금 전의 그래프를 가져와보면

정적분의 정의에 의해
이동 거리 = 빗금친곳의 면적 = 노란 사각형의 넓이 + 파란 삼각형의 넓이 =

여기서 파란 삼각형을 잘 보자.
삼각형의 중간지점에 평행선을 그어보자.
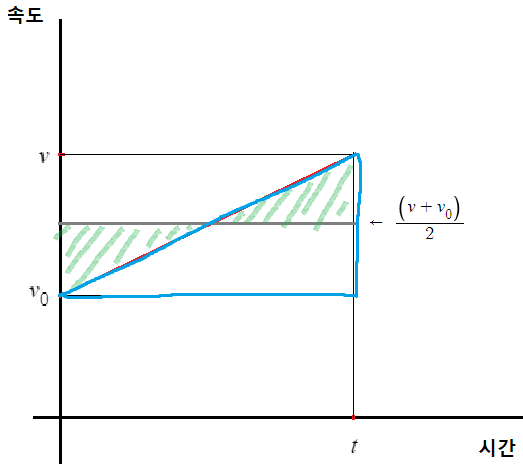
빗금 친 부분의 넓이는 같다.
저 두 삼각형은 합동일테니까
따라서 파란 삼각형의 넓이는 가로 t, 세로 (v+v0)/2인 직사각형의 넓이와 같고

따라서 여기서 빗금 친 부분의 넓이는
가로 t, 세로 (v+v0)/2 인 직사각형의 넓이와 같다.

따라서,

의 속도로 t초간 등속운동한것과 이동 거리가 같다.
쉽게 말해서, 평균적으로

의 속도로 t초간 운동했다는 뜻이다.
따라서,

는 등가속도 직선운동의 평균 속도이며, t/2초 후의 속도이다.

이를 v'이라 하면

이해를 돕기 위해 예를 들자면,
정지해 있던 물체가 T초동안 등가속도 운동을 하여 4m 움직였고,
T초 후의 속력은 2m/s라 할 때 평균 속도를 구해보자.
정지해 있었으므로 v0 = 0이고,
T초 후의 속력은 v = 2m/s이다.
따라서 평균속도는 (2+0)/2 = 1m/s이다.
이 평균 속도 개념을 잘 활용하면 문제풀이 할때
풀이식 단순화는 물론이고
풀이 난이도도 쉬워지며
문제풀이 속도도 매우 빨라진다.
- 예제 -
개념 자체의 난이도도 쉽지만은 않고
공식도 여러가지 있기때문에
꽤 어려운 문제가 자주 등장한다.
그래서 예제를 쉬운것부터 어려운것까지 준비했다.
1 )

문제풀이 단서
1. 등가속도 운동이다.
2. p점에서 가만히 놓았다 = p점에서 속력이 0이다
3. 평균속력이 v0이다.
평균속력은 (나중속도+처음속도) / 2이므로
v_0 = (v+0) / 2
따라서 v = 2v_0
따라서 답은 3번
2 )

문제풀이 단서
1. 등가속도 운동이다.
2. 평균속력과 운동시간이 언급되었다.
ㄱ)
이동거리는 평균속력 x 이동시간 이다.
따라서 이동거리 = 25 x 10 = 250m, ㄱ(o)
ㄴ)
B를 통과할때의 속력 = 나중속력
평균속력 = 초기속력과 나중속력의 평균값 = 25
초기속력이 30이므로 나중속력은 20, ㄴ(o)
ㄷ)
가속도의 방향이 운동 방향과 같다 = 속력이 증가한다
가속도의 방향이 운동 방향의 반대방향이다 = 속력이 감소한다
초기속력은 30인데 나중속력은 20이므로
속력이 감소하는 운동이다. 따라서 가속도의 방향은 운동 방향과 같지 않다. ㄷ(x)
따라서 답은 3번
3 )

문제풀이 단서
1. 등가속도 운동이다.
2. R이 최고점이다 = R에서 속력이 0이다
3. 운동 시간이 언급되어있지 않다.
ㄱ)
운동 시간에 관련된 단서가 주어져있지 않다.
따라서 이럴때는 대개 운동 시간과 관계없는 식을 이용하는것이
쉽게 풀수 있는 방법이다.
아까 등가속도운동 요약에서 등장한 시간 소거식
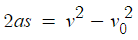
을 이용하여 가속도를 구할것이다.
우선 R에서 정지했으므로 나중속력 v=0이다.
a에 대한 식으로 만들기 위해 양변을 2s로 나누면
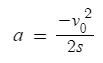
가속도의 크기를 묻고 있으므로 절댓값을 취하면 ㄱ(o)
ㄴ)
이동거리 = 평균속력 x 이동시간 이므로
이동시간 = 이동거리 / 평균속력
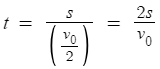
따라서 ㄴ(o)
ㄷ)
Q는 PR의 중점이다.
즉 중점에서의 속력이 평균속력이냐고 묻는것인데
결론부터 말하자면 아니다.
실수하기 십상이므로 조금 자세히 다뤄보겠다.
1. 직관적으로 봤을 때
점점 속력이 감소하는 운동이므로
점점 일정 시간에 따른 이동 거리는 감소할것이다.
그런데 평균속력 = 총 운동시간이 t라 할때 시간 t/2에서의 속력이다.
즉 시간 t/2일때는 PR의 중점보다 더 이동해있어야하므로 ㄷ은 틀렸다.
2. 그래프로 분석
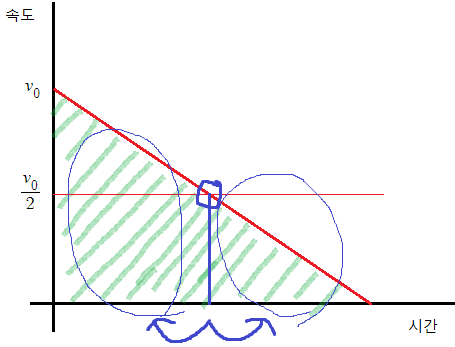
빗금친 부분의 넓이 = s이다.
속력이 v0/2인 순간에 중점을 지나려면
속력이 v0/2인 순간을 기점으로
왼쪽 빗금친 부분과 오른쪽 빗금친 부분의 넓이가 같아야한다.
근데 왼쪽 빗금친 부분의 넓이가 오른쪽 빗금친 부분의 넓이의 3배인것을 볼수있다.
따라서 ㄷ은 틀렸다.
3. 수식으로 분석
Q는 PR의 중점이므로
선분 QR의 길이는 s/2다.
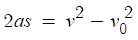
라는 식을 활용해보자.
Q를 지나는 순간의 속력을 v'이라 하면

따라서 ㄷ은 틀렸다.
따라서 답은 3번
4 )

문제풀이 단서
1. P에서 R까지 등가속도운동한다.
2. P에서 정지해있었다.
3. Q와 R사이의 거리와 각각 지점에서의 이동시간이 언급되어있다.
ㄱ)
가속도 = 속도의 변화량 / 운동시간
근데 초기속도를 제외하면 속력도 안알려주고
P에서 R까지의 거리도 안줘서 2as = v^2-v0^2도 못쓴다.
대신 Q와 R 사이의 관계가 언급되어있으니 이걸 활용할것이다.
나름의 꿀팁을 주자면
대부분 문제풀이에 쓸데없는 정보는 안준다.
즉 어딘가에 쓰라고 21m와 6초 8초라는 정보를 준것
이 정보들을 이용해서 구해볼것이다
Q와 R 사이의 거리 = 21m
Q ~ R 이동시간 = 2초
따라서 Q에서 R까지 이동할때 평균속력은 21/2 m/s이다.
t=6~t=8에서의 운동에서 평균속력이 21/2 이고
등가속도 운동이므로
t=6~t=8에서의 평균속력은 t=7에서의 속력이다.
따라서 가속도 = 속도의 변화량 / 운동시간 = (21/2) / 7 = 1.5m/s^2
따라서 ㄱ(o)
ㄴ)
ㄱ에서 가속도가 1.5인것을 구했으므로
4초일때 속력은 4a = 4 x 1.5 = 6m/s 따라서 ㄴ(x)
ㄷ)
t=2초부터 t=6초까지의 이동거리 t=2~6 사이에서의 평균속력 x 이동시간(4초)
평균속력은 t=4일때의 속력이고 a=1.5이므로 평균속력은 6m/s
따라서 이동거리는 6 x 4 = 24m, ㄷ(o)
정답은 4번
5 )

문제풀이 단서
1. 기준선 P에서 동시에 통과했고 이때의 속력이 언급되었다.
2. 등가속도 운동이다.
3. A, B가 각각 Q, R을 통과하는 순간에서의 속력의 관계가 언급되었다.
가속도 a를 구하는 문제이다.
A, B가 각각 Q, R을 통과하는 순간 속력은 B가 A의 3배라 했으므로
A가 Q를 통과하는순간의 속력을 v라 하면
B가 R을 통과하는순간의 속력은 3v이다.
운동 시간에 대한 언급이 따로 없었으니 시간 소거식을 사용할것이다.
우선 A, B의 가속도는 크기가 같고 방향이 반대인 관계라 하였으므로
A의 가속도를 a라 잡았으면 B의 가속도를 -a라 잡아야한다.
근데 A가 Q를 통과할때 B가 R을 통과한다 했으므로
B가 A보다 빠르다.
a가 가속도의 '크기' 라고 했으므로 a는 무조건 양수이고
A와 B의 가속도의 방향이 반대라 했으므로
B가 A보다 빠르다 = B는 속력이 증가했지만 A는 속력이 감소했다
즉 B의 가속도는 B의 운동방향
A의 가속도는 A의 운동방향과 반대
따라서 A의 가속도를 -a, B의 가속도를 a라 잡을것이다.
A와 B의 등가속도운동 시간소거식을 적용하면

여기서 위의 사고를 거치지 않고
A의 가속도를 a, B의 가속도를 -a라 하면 a가 음수가 나오는데
어차피 절댓값은 같기때문에 적당히 눈치껏 끼워맞출수있다.
정답은 2번
'물리I > I. 역학과 에너지' 카테고리의 다른 글
| 에너지와 열 #2 - 열역학 법칙과 열기관 (0) | 2021.07.28 |
|---|---|
| 에너지와 열 #1 - 일과 에너지, 역학적 에너지 보존 (1) | 2021.07.22 |
| 힘과 운동 #4 - 운동량 보존 법칙과 충돌 (0) | 2021.07.17 |
| 힘과 운동 #3 - 뉴턴 운동 법칙 (0) | 2021.07.16 |
| 힘과 운동 #1 - 물체의 운동 (5) | 2021.07.04 |



