
수능 확통에서
가장 출제비율이 높은게 중복조합이다.
그나마 가장 어려운거기 때문이다.
그래도 원리만 이해한다면 쉽다.
- 중복조합의 뜻 -
서로 다른 n개에서 중복을 허용하여 r개를 택하는 조합을
n개에서 r개를 택하는 중복조합이라 한다.
중복순열은 중복 허용해서 택한다음 배열까지 하는거라면
중복조합은 배열은 안하고 택하기만 하는 경우의 수를 구하는것이다.
무슨 말이냐면 한번 뽑았던걸 또 뽑아도 된다는거다.
예를 들어서
A, B, C, D, E 중 4개를 중복 허용해서 택하라 하면
ABCD 를 택할수도 있는거고
AABC 를 택할수도 있는거고
AAAA 를 택할수도 있는거다.
그러면 대체 어떻게 구하라는건지 감이 안올텐데
그래서 그나마 얘가 가장 어렵고 출제가 많이되는것이다.
- 중복순열의 계산원리 -
위에 예로 들어준것은 좀 숫자가 많으니까 쉬운걸로 가자.
A, B, C 중 4개를 중복 허용해서 택하는 경우의 수를 구해보자.

우선 4개를 택하는거니까
A, B, C가 들어갈 4자리는 마련해놓자.
물론 배열하는건 아니니까 얘네가 배열된 순서는 취급하지 않는다.
즉 자리끼리는 구별하지 않는다.
그럼 일단 아무렇게나 뽑았다고 해보자.

A, B, C중 뭔가가 뽑혀서 자리에 다 들어갔을텐데
얘네가 뭔지를 구별해줄게 필요하다.
따라서 얘네를 구별하기 위해 어떤 아이디어를 쓸거냐면
칸막이를 치는거다.
A, B, C를 구별하기 위해서는
구별해야할게 3개니까
총 2개의 칸막이가 필요하다.

만약 칸막이를 저렇게 쳤다면
칸막이 왼쪽부분에 있는건 A이고
칸막이 오른쪽부분에 있는건 C이고
두 칸막이 사이에 있는건 B 입니다. 하면 되는것이다.
A가 칸막이 오른쪽부분에 있을수도 있잖아요 할수 있는데
그건 맞는데 그냥 칸막이 왼쪽부분에 있는걸로 취급하고 계산하면 된다.
A가 칸막이 오른쪽부분에 있는게 편하면 그렇게 해도 된다.
다만 A B C 순서대로 되어있는게 직관적이니까
A B C가 순서대로 있게하기 위해서 그렇게 한것이다.
아까 자리끼리는 구별하는거 아니라 했다.
배열하는게 아니기 때문이다.
그래서 그냥 칸막이를 친다음
각각 A, B, C가 들어갈 자리라고 지정해주면 되는거다.
어차피 배열하지 않고 그냥 뽑기만 하는거기때문에
A, B, C는 불만을 갖지 않는다.
칸막이 왼쪽에 있는게 A
칸막이 오른쪽에 있는게 C
두 칸막이 사이에 있는게 B
이렇게 지정했기때문에

여기다가 칸막이만 치면
저게 A고 저게 B고 저게 C구나 구별할수 있을거니까
칸막이를 치는 경우의 수를 구하면 된다.

만약 칸막이를 위와 같이 쳤다면
뽑힌건 BCCC니까 B 1개, C 3개 인 것이다.
따라서 우리가 구할건 칸막이를 치는 경우의 수인데
최종적으로 우리가 배열할게
자리 4개와 칸막이 2개니까
칸막이가 들어갈 자리는 4+2 = 6자리이다.
근데 칸막이는 A, B, C 를 구별해주는 역할
그 이상도 이하도 아니기때문에
칸막이끼리는 구별하지 않는다.
따라서 칸막이를 치는 경우의 수는
총 6자리이고 칸막이 2개니까

이게 되는것이고
따라서 답은 15 이다.
숫자만 바꿔서 한번 더 해보자.
사과, 감, 배 중 5개를 중복 허용해서 선택하는 경우의 수는?
우선 사과, 감, 배 를 구별해내기 위해
칸막이가 필요하고
3개를 구별하는거니까 칸막이는 2개만 있으면 된다.
그리고 5개를 선택하는거니까
사과, 감, 배 가 들어갈수 있는 자리는
5자리이다.
그리고 칸막이가 2개니까
칸막이가 들어갈수 있는 자리는 총 5+2 = 7자리이다.
이 7자리중 칸막이가 들어갈 자리 2개만 택하면 되니까
답은
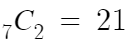
따라서 답은 21
- 일반화 : 중복조합의 계산 -
이제 원리는 알았고
식으로 일반화 하는것만 남았다.
서로 다른 n개에서 중복을 허용하여 r개를 택하는 조합을
n개에서 r개를 택하는 중복조합이라 하며,
이 중복조합의 수를 기호로 아래와 같이 나타낸다.

추가로, 중복을 허용하여 택하는거기 때문에 r>n 이어도 된다.
이를 계산하는 방법은
우선 r개를 택하는거니까 들어갈 자리 r개
n개를 구별하기 위해서 칸막이 n-1 개가 필요하니까
칸막이 포함하면 칸막이가 들어갈 자리는 r+n-1 개
그리고 칸막이만 뽑으면 되니까
r+n-1개 중 칸막이가 들어갈 자리 n-1개만 뽑으면 된다.
따라서 다음과 같이 계산하면 된다.

- 예제 -
사과, 감, 배, 귤 네 종류의 과일 중에서
중복을 허용하여 6개를 선택하려고 한다.
선택하는 경우의 수는?
4개중 6개 중복허용하여 선택하는거니까
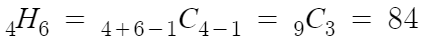
따라서 답은 84
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #1 - 이항정리의 뜻과 원리 (0) | 2021.11.29 |
|---|---|
| 중복조합 #2 - 중복조합을 이용한 경우의 수 (0) | 2021.11.27 |
| 여러가지 순열 #3 - 같은 것이 있는 순열 (0) | 2021.11.26 |
| 여러가지 순열 #2 - 중복순열 (0) | 2021.11.24 |
| 여러가지 순열 #1 - 원순열 (1) | 2021.11.23 |



