
말 그대로 순열인데
배열할 것중 같은 것이 있는 경우엔 어떻게 처리해야 하느냐를
이번에 다룰것이다.
참고로 염주순열, 같은것이 있는 원순열은 교육과정 밖이다.
- 개요 -
우리가 여태 공부한건 딱 두가지이다.
1. '서로 다른' 사람들을 원탁에 앉히는 경우의 수를 구하는 법( 원순열 )
2. '서로 다른' 것들을 중복을 허용해서 배열하는 경우의 수를 구하는 법( 중복순열 )
근데 이번엔 배열하고자 하는게 '서로 다른' 것이 아니라
같은 것도 있을수 있으니까 이 문제에 대한 해결법을 공부하는것이다.
예를 들어서
A, B, C, D 를 중복허용하지 않고 배열해서 네자리 문자를 만드는 경우의 수는
4×3×2×1 = 24 이다.
근데 A, B, C, C 를 중복허용하지 않고 배열해서 네자리 문자를 만드는 경우의 수는?
이런걸 공부할것이다.
- A, B, C, C 배열해보기 -
이 주제는 제목을 적기가 참 애매하다.
이런걸 한 단어로 정의하는 수학용어 자체가 딱히 없다.
그래서 중복순열,원순열 이런 식으로 되어있는것이 아니라
같은 것이 있는 순열 이라는 이름으로 나온것이다.
이름이 없는 이유는 간단하다.
별거 아니기때문이다.

A, B, C, C를 중복없이 배열해서 4자리 문자를 만드는거니까
대충 위와 같이 될텐데
여기서는 '중복 없이' 배열하는것이므로
각각의 문자 A, B, C, C가 갈 자리는 하나씩밖에 없고
따라서 여기서는 자리에게 문자 뭐 원하냐고 묻기보단
문자에게 자리 어디 원하냐고 묻는게 효율적이다.
A에게 묻기를
어느 자리로 갈래? 하면
갈수 있는 자리는 넷중 하나니까 A를 배열하는 경우의 수는 4이다.
B에게 묻기를
어느 자리로 갈래? 하면
갈수 있는 자리는
A가 한자리 차지했으니 세자리 남았고
따라서 B를 배열하는 경우의 수는 3이다.
이제 남은건 C 두개인데
A와 B가 그냥 아무데나 들어갔다고 쳐보자.
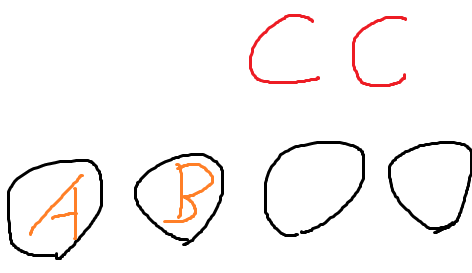
둘다 C이기 때문에
얘네 둘은 구별할수가 없다.
즉 저 상황에선
C 두개가 어차피 나머지 두자리를 꼼짝없이 가야되는데
C 끼리는 구별이 불가능하므로
여기서 C 두개를 배열하는 경우의 수는 1이다.
남은자리 두개에 남은문자 2개인데
남은 문자 2개가 구별이 안돼서
그냥 아무렇게나 넣어도 구별이 불가능하고
결국 다 똑같은것이다.
원순열과 비슷한 느낌이다.
'자리'가 'C'를 선택한다고 해보자.
자리 입장에선 'C'는 구별 불가능하기 때문에
세번째 자리가 C를 선택하는 경우의 수는 1이며
네번째 자리는 남은 문자 1개이니 꼼짝없이 경우의 수 1이다.
정리하자면,
A, B, C, C를 중복없이 배열하여 네자리 문자를 만드는 경우의 수는
A 배열하는 경우의 수 4
B 배열하는 경우의 수 3
C 두개 배열하는 경우의 수 1
따라서 4×3×1 = 12 이다.
똑같은걸 숫자만 바꿔서 연습해보자.
P, A, S, S 를 중복금지 일렬로 배열하는 방법의 수는?
P를 배열하는 방법의 수 : 4
그 후 A를 배열하는 방법의 수 : 3
나머지 S 두개를 배열하는 방법의 수 : 1
따라서 답은 4×3×1 = 12
이번엔 조금 복잡하게
A, B, C, C, D, E, E 를 중복금지 일렬로 배열하는 방법의 수는?
A를 배열하는 방법의 수 : 7
그 후 B를 배열하는 방법의 수 : 6
그 후 D를 배열하는 방법의 수 : 5
그 후 C 두개를 배열하는 방법의 수는
4자리중 2자리를 선택하는거니까
₄C₂ = 6
그 후 나머지 E 두개를 배열하는 방법의 수 : 1
따라서 답은 7×6×5×6×1 = 1260
- 다른 풀이 -
C, E를 먼저 배열해도 된다.
C 두개를 배열하는 방법의 수는
7자리중 2자리를 선택하는거니까
7C2 = 21
그 후 E를 배열하는 방법의 수는
5자리중 2자리를 선택하는거니까
5C2 = 10
나머지 A,B,D를 세자리에 배열하는 경우의 수는
3×2×1 = 6
따라서 답은 21×10×6 = 1260
- 심화 : 최단거리로 가는 경우의 수 -

A에서 출발하여 B로 최단거리로 가는 경우의 수는?
이것도 그냥 같은 것이 있는 순열인데
문제 생김새만 바꿔서 나온것이다.
우선 최단거리로 가려면
중간에 딴길로 새면 안된다.
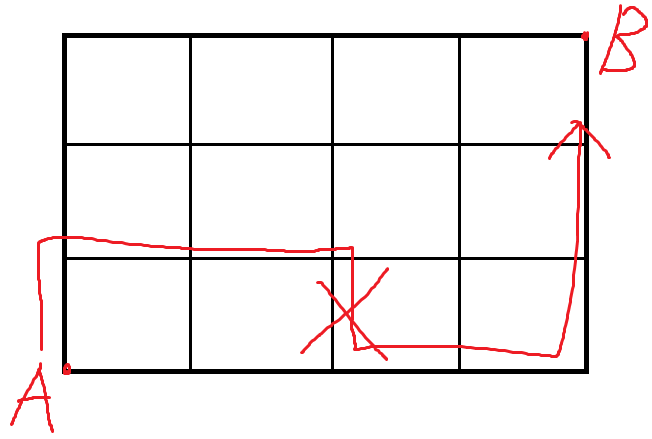
즉 이런 경우는
B에서 멀어지는 방향으로 움직이는 때가 있기 때문에
이때는 최단거리가 아니고 이런경우는 취급하지 않는다.
따라서 A에서 B로 최단거리로 가려면
무조건 B에 가까워지는 방향으로 가야한다.
A에서 B로 가려면
오른쪽으로 4칸, 위로 3칸 가야한다.
그러면 A→B 로의 이동경로에서
1. 위로 가는 경우
2. 오른쪽으로 가는 경우
이 두개로만 구성되어야 한다는것이다.
이제 같은것이 있는 순열처럼 하면 된다.
위로 가는 경우를 ↑ 라 하고
오른쪽으로 가는 경우를 → 라 하자.
그러면 ↑ 4개와 → 3개를 배열한게
A에서 B로 가는 최단거리의 경로가 되는 것이다.
즉 ↑, ↑, ↑, ↑, →, →, → 를 배열하는 경우의 수를 구하면 된다.
→ 4개를 배열하는 경우의 수는
7자리중 4자리 가야되니까 7C4 = 35
나머지 ↑ 3개를 배열하는 경우의 수는
남은게 3자리니까 선택의 여지 없이 1
따라서 이 문제의 답은 35이다.
다른 방법도 있다.

이런식으로 푸는건데
엄청난 꼼수같지만 사실 아주 간단한 논리이다.
저 숫자들은 각각 경우의수들을 적은것인데
하나씩 해석해주겠다.

우선 이 부분만 떼어서 보자.
A에서 출발한다.
그럼 위로가는 경우 1
오른쪽으로 가는 경우 1
그럼 위의 사진에서 숫자 1의 정체는 알아냈다.
그럼 2는 어디서 나온건가?

저 숫자 2가 써진 지점을 향해서
가는 경우는
왼쪽에서 오거나
아래에서 오거나
둘중 하나이다.
그렇지 않으면 최단경로가 아니기 때문에 이건 취급하지 않는다.
근데 위쪽에서 오는 경우의 수 : 1
아래쪽에서 오는 경우의 수 : 1
경우의 수를 계산할때
한 사건에서 동시에 일어날수 있는일이면 곱셈연산
그렇지 않으면 덧셈연산 한다고 배웠었다.
여기선 위쪽에서 오면서 아래쪽에서 오는건 불가능한 경우이기 때문에
덧셈연산 해야하는거고
따라서 위쪽에서 오는 경우의 수와
아래쪽에서 오는 경우의 수를 더해서
1+1 = 2 라고 계산된것이다.

이젠 감이 오나?
A에서 위로만 가는 경우의 수는 하나밖에 없으니 1인거고
A에서 오른쪽으로만 가는 경우의 수도 하나밖에 없으니 1인거고
각 지점에서의 값은
각 지점을 향해 오는 경우의 수가
왼쪽에서 오거나
아래쪽에서 오거나 이므로
이 둘을 더해서 구하는것이고
따라서 3의 정체는 1+2 = 3
6의 정체는 3+3 = 6
이를 반복하면

A에서 B로 가는 최단경로의 수를 구할수 있다.
이 풀이의 장점은
1. 실수할일 거의 없음
2. 쓰는 방법은 쉬은데 이걸로 안풀리는 문제가 없음
- 예제 -
난이도 조금 올라간 예제문제와 함께 마무리하겠다.

1. 첫번째 풀이 : 정석풀이
우선 A에서 출발하여 P를 지나서 B까지 간다는건
가는 도중에 '무조건' P를 지나야 한다는것이다.
그리고 그 와중에도 최단경로로 가야하기 때문에
B에서 멀어지는 방향으로 움직이면 안된다.
즉 오른쪽으로 가는 것과
위쪽으로 가는 것을 배열하되
오른쪽으로 두번가고 위쪽으로 두번간 지점을 지나도록 배열해야한다.
그러면 어렵게생각하지 말고
그냥 차례차례 하면 된다.
P에서 B까지도 어차피 최단경로로 가야하므로
A에서 P까지 최단경로로 가는 경우의 수와
P에서 B까지 최단경로로 가는 경우의 수를
그냥 곱해주면 된다.
A에서 P에 도달하는 각각의 경우의 수에 대해
또 P에서 B까지 최단경로로 가도록 찢는거니까
결론적으로 두 경우의 수를 곱한게 답이 되는것이다.
이래도 이해가 안될때를 대비해 부연설명해주자면
A에서 P로 가는 경우와
P에서 B로 가는 경우는
'A에서 B로 가는 사건'에서 동시에 일어나기 때문에
A에서 P로 가는 사건과 P에서 B로 가는 사건을 곱셈연산 해야한다.
A에서 P로 가는 최단경로의 경우의 수는
오른쪽으로 가는거 2번
위로가는거 2번을 배열하면 되고
오른쪽으로 가는걸 →, 위로가는걸 ↑라 하면
→, →, ↑, ↑를 배열하는거고
따라서 A에서 P로 가는 최단경로의 경우의 수는
→ 두개 배열하는 경우의 수 : ₄C₂ = 6
나머지 ↑ 두개 배열하는 경우의 수 : 선택의 여지 없이 1
따라서 6×1 = 6
그리고 P에서 B로 가는 최단경로의 경우의 수는
→, →, →, ↑를 배열하는 경우의 수이고
이것은 ↑ 하나만 자리 지정해주면
나머지 → 3개는 알아서 남는자리 갈테니
↑ 배열하는 경우의 수 : 4
나머지 → 3개 배열하는 경우의 수 : 1
따라서 4×1 = 4
따라서 경우의 수는 6×4 = 24
따라서 답은 5번
2. 두번째 풀이
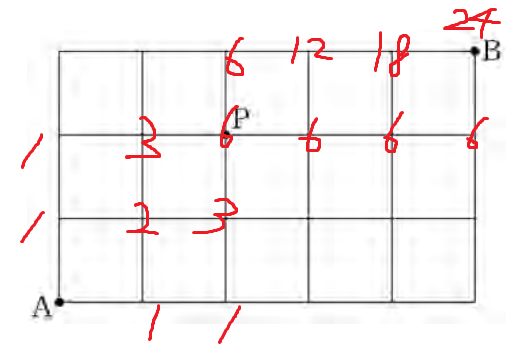
따라서 경우의 수는 24
따라서 답은 5번
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #1 - 이항정리의 뜻과 원리 (0) | 2021.11.29 |
|---|---|
| 중복조합 #2 - 중복조합을 이용한 경우의 수 (0) | 2021.11.27 |
| 중복조합 #1 - 중복조합의 뜻과 계산 원리 (1) | 2021.11.26 |
| 여러가지 순열 #2 - 중복순열 (0) | 2021.11.24 |
| 여러가지 순열 #1 - 원순열 (1) | 2021.11.23 |



