확률과 통계의 첫번째 내용이다.
순열 자체의 기본 개념은 공통수학에서 다루기 때문에
여기서는 전부 안다고 가정하고 진행한다.
- 원순열 -
원순열 : 서로 다른 것을 원형으로 배열하는 순열
예를 들자면

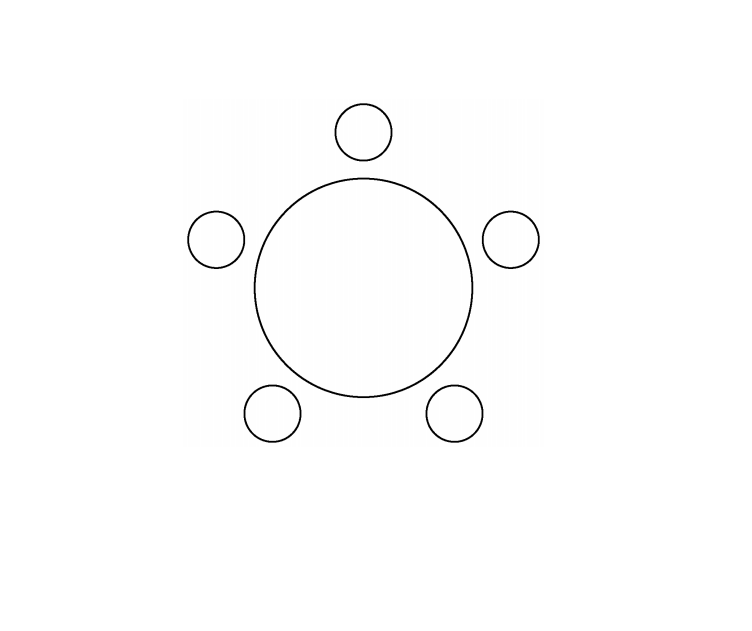
사람 5명이 있고
원형 탁자에 의자 5개가 놓여있다고 해보자.
여기서 사람 5명을 저 5자리에 앉히는 경우의 수를 구하는 방법을
이번에 배우는것이다.
여기서 중요한건
의자는 서로 구별할 수 없다. 즉 다 같은 의자이다.
이것이 이 글 전반적으로 이용될 내용이니 알아두자.
의자를 서로 구별할수 있느냐 없느냐에 따라 달라진다.
무슨 말인지는 천천히 설명해줄것이다.
사람 A, B, C, D, E가 있다고 해보자.
그럼 A가 갈곳은 5곳이다.
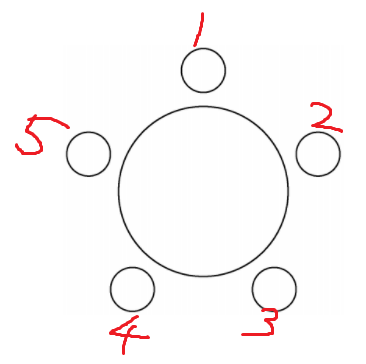
그럼 A를 앉히는 경우의 수는 5일까?
답부터 하자면 무조건 1이다.
왜냐면 A를 저 5개의 의자에 각각 앉힌 다음
이것들을 비교해보겠다.
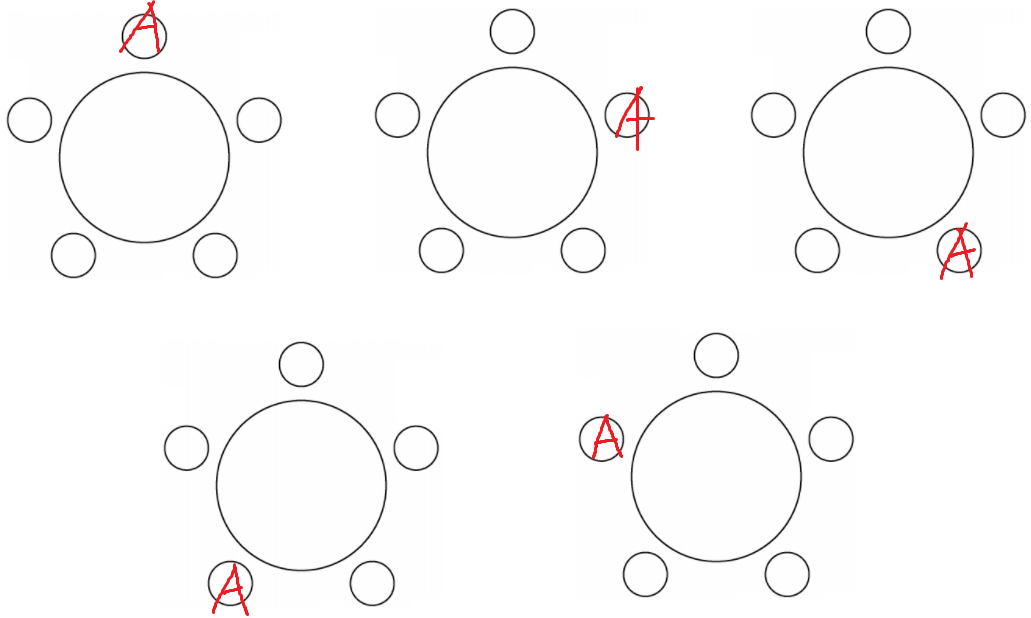
5개 다 다른경우 같지만
사실은 모두 같은 경우이다.
왜냐면 '회전'시키면 똑같기때문이다.
아까 의자끼리는 구별이 불가하다 했었다.

회전시키면 결국 다 같은 경우이기 때문에
A가 앉는 경우의 수는 1인것이다.
즉 A가 어디 앉든 똑같다.
그냥 A가 앉았다. 라는 의미 그 이상도 이하도 아니다.
여기까지 요약하자면
A 어디앉을래?
해서 A가 선택한 자리는
선택한 자리가 어디던간에 어차피 회전시키면 다 똑같은거기 때문에
구별이 불가능하다.
따라서 이걸 다른 경우로 취급하지 않고 모두 같은 경우로 취급한다.
즉 첫 사람이 첫번째 자리를 선택하는 경우의 수는 무조건 1이다.
다음으로 B를 앉혀보자.
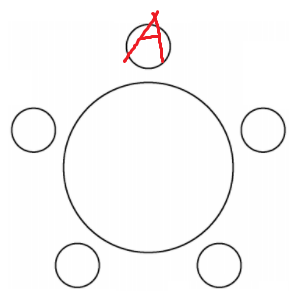
이때 B가 앉는 경우의수도 1일까?
그건 아니다.
A가 앉은 순간
더이상 회전시켜도 똑같은 경우가 되는게 아니기 때문이다.
예를 들어서, B가 말하기를
"난 A 바로 왼쪽에 앉을래." 라고 했다면
B가 앉을곳은 여기 하나밖에 없는거 아닌가?
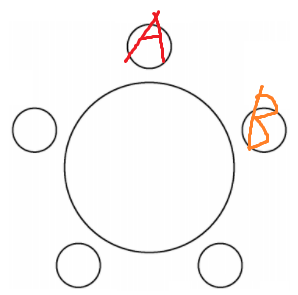
만약 B가 앉는 경우의수도 1이라면
즉 회전시켜서 결국 같은 경우인 것이라면
B가 어디 앉든
B가 원하는 자리인 'A 바로 왼쪽'에 앉게 되어야 한다.
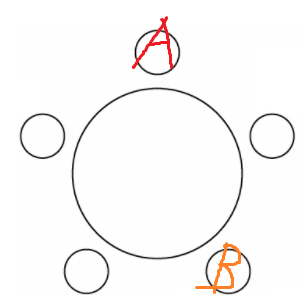
근데 B를 여기 앉혀버린다면
이 탁자는 아무리 회전시켜도
절대 B는 A의 왼쪽에 있을수 없다.
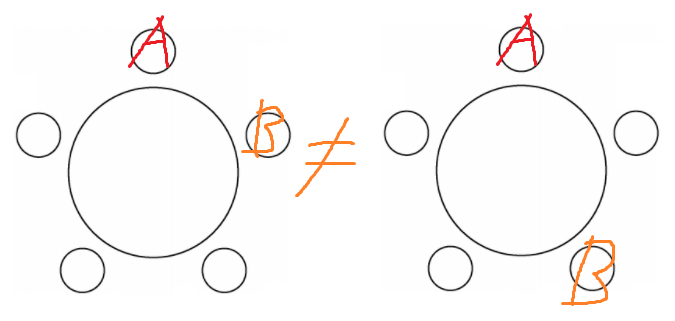
이 둘은 다른 경우라는 뜻이다.
즉 B가 A의 바로 왼쪽에 앉는것과
B가 A로부터 왼쪽으로 2칸 떨어진곳에 앉는것은
다른 경우이다.
B는 자기를 A 바로 왼쪽에 앉혀달라 했는데
두칸 떨어진곳에 앉혀주면 B는 불만이 생길것이다.
왜 이런 차이가 생길까?
왜 A가 처음에 앉는 경우의 수가 1이었는지를 다시 상기해보자.
A가 선택할수 있는 5개의 의자는 '구별이 불가능'하며
따라서 A가 어디에 앉든 회전시키면 결국 같은 경우이기 때문에
A가 앉는 경우의 수가 1이었던것이다.
그런데 A가 앉는 순간
구별 불가능하던 의자들은
이젠 '구별 가능한' 의자가 된것이다.
각각의 의자에 다음과 같이 이름을 붙일수 있을거 아닌가?
A 바로 왼쪽 자리, A로부터 왼쪽으로 두칸 떨어진 자리, A 바로 오른쪽 자리 등
즉 여기서 B가 앉는 자리를 선택하는 경우의 수는
남은 의자가 4개이고
이 의자는 서로 구별 가능한거니까 결론적으로 4가 되는 것이다.
같은 논리를 적용하면
C가 앉는 경우의 수는 3이며
D가 앉는 경우의 수는 2
E가 앉는 경우의 수는 1이다.
따라서

이런 원형 탁자에 사람 5명을 앉히는 경우의 수는
1 × 4 × 3 × 2 × 1 = 24 이다.
똑같은걸 숫자만 바꿔서 다시 해보겠다.
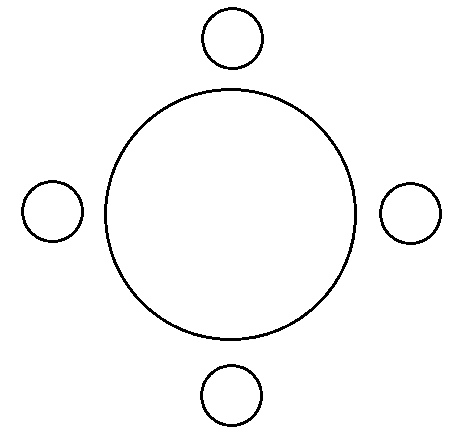
원형 탁자에 4개의 똑같은 의자가
같은 간격으로 떨어져있다.
이때 사람 4명을 앉히는 경우의 수는?
(단, 회전하여 일치하는 것은 같은 것으로 본다.)
사람 4명을 A, B, C, D 라고 하겠다.
A, B, C, D를 차례로 앉히겠다.
A : 어디앉아도 똑같음. 즉 아무데나 앉음 ( 경우의수 : 1 )
B : 3자리 남았네? 그럼 셋중에 하나 골라 앉아야겠다. ( 경우의수 : 3 )
C : 2자리 남았네? 그럼 둘중에 하나 골라 앉아야겠다. ( 경우의수 : 2 )
D : 한자리밖에 안남았네? 그럼 선택의 여지 없이 여기 앉아야겠다. ( 경우의수 : 1 )
따라서 경우의 수는 1×3×2×1 = 6 이다.
- 일반화 -
원순열의 경우, 회전하여 일치하는것은 같은 것으로 보기 때문에
한 자리를 아무데나 고정시킨 후, 나머지를 일렬로 배열하는 경우의 수를 구하면 된다.
원래는 구별 불가능한 의자였지만
한 자리가 고정된 후엔 각각의 의자가 특징이 생기기 때문에
구별 가능한 의자가 되는것이고, 따라서 여기부턴
나머지를 일렬로 배열하는 경우의 수를 구하면 된다.
수식으로 표현하면,
서로 다른 n개를 원형으로 배열하는 원순열의 수는 다음과 같다.
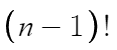
처음 앉는 사람은 어디 앉든 똑같기때문에 1이고
나머지는 그대로 n-1개를 배열하면 되기 때문에 (n-1)! 인 것이다.
- 심화 1 : 탁자가 원이 아니라 다각형인경우 -
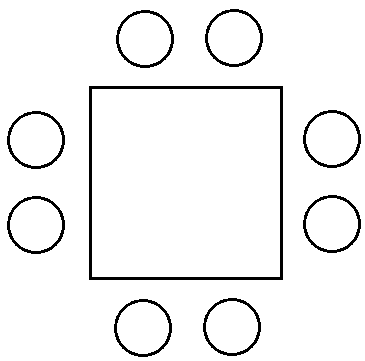
정사각형인 탁자가 있고
이런 탁자에 8명을 앉히는 경우의 수를 구해보자.
사람을 A, B, C, D, E, F, G, H라고 하겠다.
A를 먼저 앉힐건데
여기서 A가 앉는 경우는 1이 아니다.
왜냐면 회전시켜도 같지 않은 경우가 있기 때문이다.
A가 말하기를,
"나는 탁자 모서리의 왼쪽 부분에 앉고 싶다."
라고 했다면
A가 앉을수 있는곳은
8자리 전부가 아니라
아래 4자리이다.
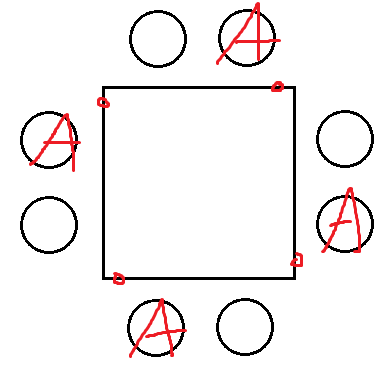
A가 앉고싶은곳은
'탁자 모서리의 왼쪽 부분에 있는 의자' 이기 때문이다.
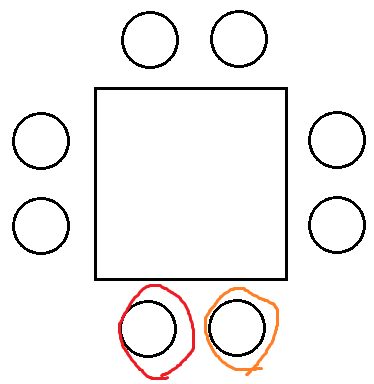
즉 왼쪽부분과 오른쪽부분에 앉는 경우는 다르게 취급해야한다.
오른쪽 부분에 앉는다면
'탁자 모서리의 오른쪽 부분에 있는 의자' 라는 곳에 앉는것이기 때문이다.
이 탁자에서
'탁자 모서리의 왼쪽 부분에 있는 의자' 는 4개이며
'탁자 모서리의 오른쪽 부분에 있는 의자' 도 4개이다.
탁자는 정사각형 모양이기 때문에
탁자 모서리의 왼쪽 부분에 있는 의자 끼리는 서로 구별이 불가능하며
탁자 모서리의 오른쪽 부분에 있는 의자 끼리도 서로 구별이 불가능하다.
하지만 탁자 모서리의 왼쪽 부분에 있는 의자와
탁자 모서리의 오른쪽 부분에 있는 의자는 구별이 가능하다.
따라서 여기서 A가 앉는 경우의 수는
탁자 모서리의 왼쪽 부분에 있는 의자에 앉던지
탁자 모서리의 왼쪽 부분에 있는 의자에 앉던지
둘중 하나이다.
즉 A가 앉는 경우의 수는 2이다.
이제 A를 앉히고 나면
모든 의자가 구별 가능한 의자가 되기 때문에
나머지 7명을 그냥 일렬로 배열하면 된다.
7명을 일렬로 배열하는 경우의 수는 7×6×5×4×3×2×1 이므로
최종적으로 우리가 구하고자 하는
사람 8명을 이 탁자에 앉히는 경우의 수는
2×7×6×5×4×3×2×1 이다.
- 심화 2 : 이웃하게 앉히는 경우 -
이건 예제문제를 풀어주면서 설명해주는게 매끄러울거같다.

1. 하던대로 풀기
A : 아무데나 앉아도 똑같기때문에 아무데나 앉는다. ( 경우의수 : 1 )
B : 난 A와 이웃해야하기 때문에 A의 왼쪽자리나 A의 오른쪽자리에 앉아야한다.
따라서 A의 왼쪽자리와 A의 오른쪽자리중 하나를 선택해서 앉는다. ( 경우의수 : 2 )
C : 남은 자리가 4개니까 넷중 하나 선택해서 앉는다. ( 경우의수 : 4 )
D : 남은 자리가 3개니까 셋중 하나 선택해서 앉는다. ( 경우의수 : 3 )
E : 남은 자리가 2개니까 둘중 하나 선택해서 앉는다. ( 경우의수 : 2 )
F : 한자리밖에 안남아서 선택의 여지가 없다. ( 경우의수 : 1 )
따라서 경우의 수는 1×2×4×3×2×1 = 48 이다.
따라서 답은 2번이다.
2. A와 B를 하나로 묶기
A와 B는 이웃해야하기 때문에
일단 A와 B 에게 묻는다. 너네 어디 앉을거냐?
여기서 A+B는 어디 앉든 상관이 없다.
어차피 회전시키면 똑같기 때문이다.
하지만 A와 B가 서로 자리를 바꿀수는 있다.
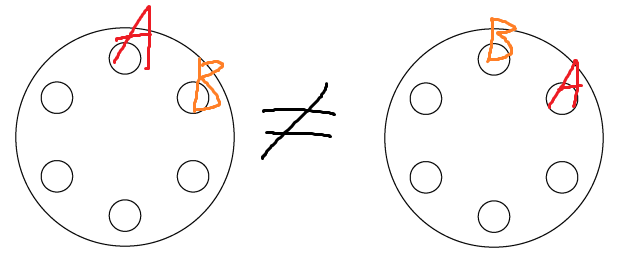
A와 B가 이웃하는 경우의 수는 두가지밖에 없다.
A가 B 왼쪽에 있던가
A가 B 오른쪽에 있던가
둘은 다른 경우이기 때문에
우선 A와 B가 앉을 두 자리를 '선정'하는 경우의 수는 하나 뿐이지만
이 선정된 자리에 A와 B가 앉을 때
A가 B 왼쪽에 있느냐, 오른쪽에 있느냐는 다른 경우이고
따라서 이 둘을 다르게 취급해야한다.
따라서 일단 A와 B가 앉을 두 자리를 '선정' 하는 경우는 1이지만
선정된 두 자리에서 A와 B가 앉는 경우의 수는 2이기 때문에
결론적으로 A와 B를 앉히는 경우의수는 2가 되는것이다.
이제 나머지는 똑같이 하면 된다.
C : 네자리 남았으니 4
D : 세자리 남았으니 3
E : 두자리 남았으니 2
F : 한자리 남았으니 선택의 여지 없이 1
따라서 2×4×3×2×1 = 48
따라서 답은 2번
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #1 - 이항정리의 뜻과 원리 (0) | 2021.11.29 |
|---|---|
| 중복조합 #2 - 중복조합을 이용한 경우의 수 (0) | 2021.11.27 |
| 중복조합 #1 - 중복조합의 뜻과 계산 원리 (1) | 2021.11.26 |
| 여러가지 순열 #3 - 같은 것이 있는 순열 (0) | 2021.11.26 |
| 여러가지 순열 #2 - 중복순열 (0) | 2021.11.24 |



