
- 이항정리의 뜻 -
이항정리 에서
'정리' 는 '피타고라스정리' 에서의 정리와 같은뜻의 정리이다.
영어로는 Theorem
그리고 '이항' 이라는 말은
'항이 두개' 라는 뜻이다.
따라서 이항정리의 뜻은
두개의 항으로 이루어진 것의 거듭제곱을 전개하는 것

a+b는 a, b 두개의 항으로 이루어진 거고
이것의 합의 거듭제곱을 전개하는것을 배울것이다.
항이 3개 이상인건 다항정리라고 하는데
교육과정 밖이니 우리는 이항정리만 할줄알면 된다.
그리고 우리는 거듭제곱의 지수인 n이 자연수인것만 다룬다.
- 이항정리 직접 해보자 -
우선 간단한것부터 해보자.

이걸 이항정리, 즉 전개하면?

다음으로

이걸 이항정리, 즉 전개하면?

여기서 세제곱의 전개식을 분석해보자.
a³ 의 계수는 1이다.
따라서 a³ 은 1개 있었다.
a²b 의 계수는 3이다.
따라서 a²b 는 3개 있었다.
ab² 의 계수는 3이다.
따라서 ab² 는 3개 있었다.
b³ 의 계수는 1이다.
따라서 b³ 은 1개 있었다.
그리고 (a+b)³은 아래와 같이 쓸수도 있다.

이 식을 통해 a³ 이 왜 1개 있었는지 알아보자.

a+b 를 세번 곱한건데
여기서 전개할때
a와 b 중 하나를 선택해서 그것과 곱해질것인데
전부 a를 선택했기 때문이다.
즉 a³ 은
전개 과정에서 a와 b중 선택할때
전부 a를 선택한것의 결과물 임을 알수있다.
그리고 계수가 1인건
전부 a를 선택하는 경우의 수가 1이기 때문이다.
b³ 도 같은 논리로
전부 b를 선택한것의 결과물인데
전개 과정에서 a와 b중 선택할때
전부 b를 선택하는 경우의 수가 1이기 때문에 계수가 1인것이다.

이제 a³ 과 b³ 의 정체는 알아냈고
3a²b 와 3ab²의 정체를 알아내보자.

a와 b 중 하나를 선택해서 그것과 곱해질것인데
a가 두번, b가 한번 선택되었기 때문에 a²b가 나온것이다.
근데 a+b를 '3번' 곱하는거기 때문에
선택의 기회는 총 3번이다.
근데 'a를 2번' 선택하고 'b를 1번' 선택한거다.
이걸로 나올수 있는 경우의 수는 aab, aba, baa
따라서 3개이다.
그래서 a²b 의 계수가 3인것이다.
ab² 도 같은 논리로 계수가 3이다.
이제 종합해보자.

계수 : 이 곱셈 조합이 선택되는 경우의 수
a³ = (a+b)³ 를 전개하는 과정에서 a가 3번 선택되었다.
그리고 그럴 수 있는 경우의 수는 1이다.
3a²b = (a+b)³ 를 전개하는 과정에서 a가 2번, b가 1번 선택되었다.
그리고 그럴 수 있는 경우의 수는 3이다.
3ab² = (a+b)³ 를 전개하는 과정에서 a가 1번, b가 2번 선택되었다.
그리고 그럴 수 있는 경우의 수는 3이다.
b³ = (a+b)³ 를 전개하는 과정에서 b가 3번 선택되었다.
그리고 그럴 수 있는 경우의 수는 1이다.
이해를 돕기 위해 이 식을 조금 다르게 쓸것이다.


그냥 각각 지수만 붙여준거다.
이 식이 의미하는 바는
어떻게 곱해도 a와 b중 하나는 곱해질거고
둘중 하나 선택해서 곱하는 이 행위를
총 3번 하니까
총 3번 곱해질거라는 것이다.
즉

a와 b가 들어가야할 세자리는 마련되어있고
여기에 a나 b를 선택해서 넣는것이다.
단 aab, aba, baa 는 순서는 다르지만 결과는 똑같은거기 때문에
같은 경우로 취급해야한다.
즉 a, b 의 개수만 뽑으면 되지 배열할 필요는 없다는것이다.
어차피 구별이 안되기 때문이다.

a+b 의 세제곱을 전개하는 과정에서
a와 b중 선택할 수 있는 기회는 3번인데
a는 3번 선택되었고, b는 0번 선택되었습니다.
즉 아까 그림에서 제시한 것에서
a가 3번, b가 0번 선택되는 경우의 수를 구하면
그게 곧 a³ 의 개수가 되고
a³ 의 개수가 곧 a³ 의 계수 가 되는것이다.
a를 3번, b를 0번 선택하는 경우의 수는
a만 3번 선택되는 경우
또는 b가 0번 선택되는 경우
따라서 아래와 같다.

따라서 a³의 정체는 다음과 같다.
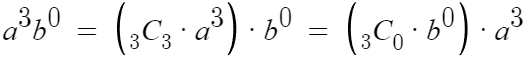

a+b 의 세제곱을 전개하는 과정에서
a와 b중 선택할 수 있는 기회는 3번인데
a는 2번 선택되었고, b는 1번 선택되었습니다.
a를 2번, b를 1번 선택하는 경우의 수는
어차피 a와 b중 하나 선택하는거니까
a를 2개 선택하면 b는 알아서 1개 선택된다.
즉 a를 2개 선택하는 경우
또는 b를 1개 선택하는 경우
따라서 아래와 같다.

따라서 3a²b¹의 정체는 다음과 같다.


a+b 의 세제곱을 전개하는 과정에서
a와 b중 선택할 수 있는 기회는 3번인데
a는 1번 선택되었고, b는 2번 선택되었습니다.
a를 1번, b를 2번 선택하는 경우의 수는
어차피 a와 b중 하나 선택하는거니까
a를 1개 선택하면 b는 알아서 2개 선택된다.
즉 a를 1개 선택하는 경우
또는 b를 2개 선택하는 경우
따라서 아래와 같다.

따라서 3a¹b²의 정체는 다음과 같다.


a+b 의 세제곱을 전개하는 과정에서
a와 b중 선택할 수 있는 기회는 3번인데
a는 0번 선택되었고, b는 3번 선택되었습니다.
a를 0번, b를 3번 선택하는 경우의 수는
a가 0번 선택되는 경우
또는 b만 3번 선택되는 경우
따라서 아래와 같다.

따라서 b³의 정체는 다음과 같다.

정리하면, (a+b)³ 의 이항정리는 다음과 같다.

- 이항정리의 일반화 -
이제 원리는 이해했을거고
일반화 해보자.

이것의 이항정리를 구해보자.
a와 b중 하나를 택하는 행위를 n번 한다.
택할게 a, b 둘중 하나기 때문에
a를 몇개 택할지만 정해주면 b의 개수도 알아서 정해지고
그러면 항이 정해지게된다.
즉 a를 몇개 택할지만 구하면 되고
그것의 경우의 수가 전개식에서의 각 항의 계수이다.
따라서 다음과 같이 될것이다.

이제 여기서 한걸음 더 나가서
일반항을 구해보자.
r 번째 항의 값은?
n개중 a가 r개 선택된것

- 예제 -

우선
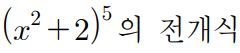
우선 여기에서 '이항정리' 문제임을 알 수 있으며
5제곱인데 x^6 이라는건
5번중 x² 가 3번 선택되었고
5번중 2가 2번 선택되었다는것이다.
따라서 x^6 이 포함된 항을 구해보면
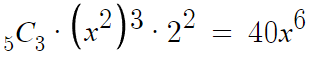
따라서 답은 40
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #2 - 이항계수의 성질과 파스칼의 삼각형 (0) | 2021.12.01 |
|---|---|
| 중복조합 #2 - 중복조합을 이용한 경우의 수 (0) | 2021.11.27 |
| 중복조합 #1 - 중복조합의 뜻과 계산 원리 (1) | 2021.11.26 |
| 여러가지 순열 #3 - 같은 것이 있는 순열 (0) | 2021.11.26 |
| 여러가지 순열 #2 - 중복순열 (0) | 2021.11.24 |



