
신기하게 생긴게 등장했는데
이것에 대해 다룰것이다.
- 이항계수의 정의 -
이항정리의 전개식에서
각 항의 계수를 이항계수라 한다.

이게 이항정리 한건데

밑줄친 것들이 이항계수라는 뜻이다.
- 이항계수의 성질 -
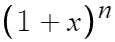
이걸 이항정리 해보자.

이렇게 될 것이다.
여기서 x=1 이라 해보자.

그러면 이항계수의 합 꼴로 식이 바뀌고
이것의 값은

아까 1+x를 이항정리했는데 x=1 이니까 결국

이 식이 유도된다.
1. n 거듭제곱의 이항정리에서
이항계수의 합은 2ⁿ 이다.
여기서 편의상 n=7 이라 하고 나머지 성질도 찾아보겠다.

그러면 위 식이 성립한다.
근데 '조합' 의 성질에 의해

짝지은 것들끼리는 서로 같다.


따라서 반으로 딱 갈라주면
왼쪽 부분과 오른쪽 부분이 같다는 결론에 이르게 된다.
즉 왼쪽 부분의 합 = 오른쪽 부분의 합 = 전체의 절반
근데 전체의 값은 2의 5제곱이니까
왼쪽부분의 합은 2의 5제곱의 절반인 2의 4제곱이 된다.
오른쪽부분의 합도 같은 논리로 2의 4제곱이 된다.
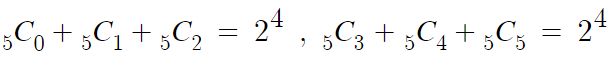
단 주의할 부분은
이거는 n=5였으니까 전체의 절반이 된것이다.

즉 n이 홀수라서 이와 같이 정확히 반으로 갈라진것이다.
만약 n이 짝수라면? n=4라 하겠다.


우선 절반으로 가른것을 기준으로
왼쪽 부분의 합과 오른쪽 부분의 합은 같다.
하지만 이것의 값이 전체의 절반은 아니다.
왜냐면 가운데에
왼쪽 부분에 속하지도 않으면서
오른쪽 부분에 속하지도 않는
₄C₂ 가 존재하기 때문이다.
따라서 다음과 같이 요약된다.
n이 홀수인 경우
왼쪽부분의 합 = 오른쪽부분의 합 = 전체합의 절반
n이 짝수인 경우
왼쪽부분의 합 = 오른쪽부분의 합 = 전체합에서 가운데부분값 빼준것의 절반
그리고 한가지 더 찾아낼 수 있는데
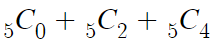
이것의 값은 무엇인가?
즉 짝수번째 이항계수의 합은 얼마인가?
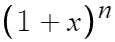
이것의 이항정리에서
x=-1 이라 해보자.
그러면 다음 식이 완성된다.
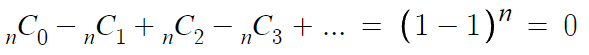
좌변의 -부호 붙은애들을 전부 이항하면
다음과 같은 결론을 얻는다.
따라서 다음과 같은 결론을 얻는다.

짝수번째 이항계수의 합 = 홀수번째 이항계수의 합 = 전체합의 절반
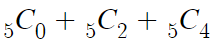
따라서 이것의 값은
홀수번째 이항계수의 합이므로 전체합인 2의 5제곱 의 절반
따라서 2의 4제곱, 2⁴ 이다.
숫자만 바꾼 예제문제 몇개만 풀어보고 다음으로 넘어간다.
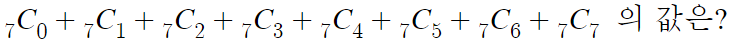
7 거듭제곱의 이항계수의 합을 구하라고 한다.
그것은 (1+x)ⁿ 에서 x=1이라 놓고 n=7이라 놓고 유도 가능하며
아까 해준것에서 숫자만 바꾼거다.
답은 2^7 (2의 7제곱)

아까 문제의 식에서 딱 반으로 잘랐을때
오른쪽 부분의 합을 구하라는거다.
n이 홀수일때는 오른쪽 부분의 합 = 전체합의 절반 이라 했는데
이 문제에선 n=7로 홀수이다.
따라서 답은 2의 7제곱의 절반인
2의 6제곱이다. 2^6
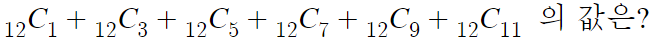
(1+1)ⁿ 의 이항정리에서
n=12 일때의 이항계수 중
짝수번째 이항계수들의 합을 구하라 한다.
짝수번째 이항계수의 합은 전체합의 절반이다.
전체합은 n=12이므로 2^12, 2의 12제곱이다.
따라서 답은 2의 12제곱의 절반인
2의 11제곱 이 된다.
- 파스칼의 삼각형 -
이항계수를 배열하여 삼각형 모양으로 나타낸 것을
파스칼의 삼각형이라 한다.
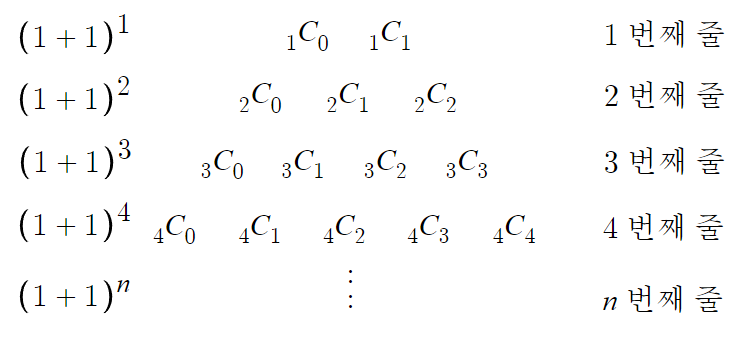
파스칼의 삼각형 만드는법은 간단하다.
(1+1)의 거듭제곱의 이항정리의 이항계수를
위와 같이 적는다.
이게 왜 특별하냐면
조합의 성질을 설명하는데에 있어서 가독성좋은 도구이다.
1. n번째 줄의 합은 곧 이항계수의 합이기 때문에,
n번째 줄의 합은 2ⁿ 이다.
2. 파스칼의 삼각형은 좌우 대칭이다. 따라서 아래 식이 성립한다.
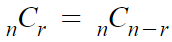
3. 각 수는 그 수의 왼쪽 위와 오른쪽 위에 있는
두 수의 합과 같다.

빨간 동그라미 친것의 값은
녹색 동그라미 친것들의 합과 같다는 말이다.
이것은 파스칼의 삼각형 어느 지점에 찍어도 성립한다.
그럼 일반화를 위해 n번째줄과 n+1번째줄의 관계를 보자.

n번째 줄의 r번째 항과 n번째 줄의 r+1번째 항의 값을 더한게
n+1번째 줄의 r+1번째 항의 값을 더한것과 같다.
따라서 다음과 같이 일반화된다.
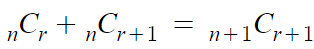
이를 증명해보자면 다음과 같다.
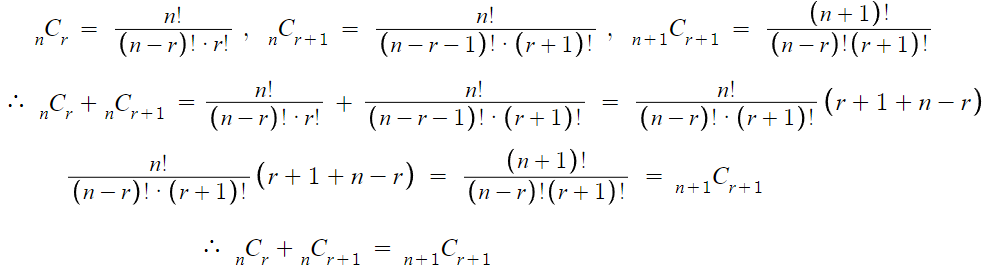
예제 하나 가볍게 풀어보자.
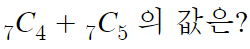
첫번째 풀이 : 조합의 성질을 이용

두번째 풀이 : 그냥 계산
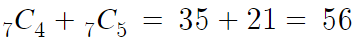
따라서 답은 56
4. 하키 스틱 패턴
파스칼의 삼각형에서 가장 신기한 성질이다.
바깥쪽 1에서 시작하여 대각선 방향으로 수를 더하면
아래행의 안쪽 하키 스틱 모양에 있는 수가 된다.
무슨말인지 모를텐데
왜 이름이 하키스틱패턴이냐면
하키스틱의 모양을 떠올려보자.

하키스틱은 대충 이런식으로 생겼다.
이제 해보겠다.
바깥쪽 1에서 시작하여 대각선 방향으로 수를 더할것이다.
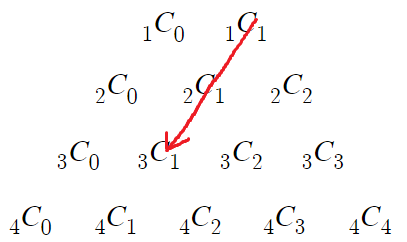
첫번째줄의 1부터 시작해서
이런 방식으로 세번째줄까지 더할것이다.
그리고 이 값은
아래행의 안쪽 하키스틱 모양
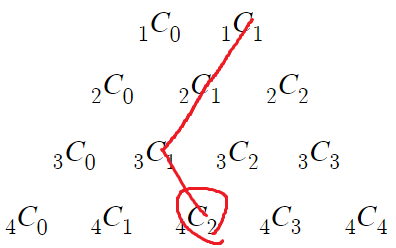
즉 대각선으로 내려가되
하키스틱 모양을 만들기 위해 마지막에 방향만 반대로 꺾어서 한칸 내려가면
그게 모두 더한 결과값이라는 말이다.
₁C₁ = 1 이고
₂C₁ = 2 이고
₃C₁ = 3 이고
₄C₂ = 6 이므로
1+2+3 = 6
따라서 성립한다.
이는 바깥쪽 1에서부터 시작하여
대각선 아래방향으로 수를 더하는 모든것에 성립한다.
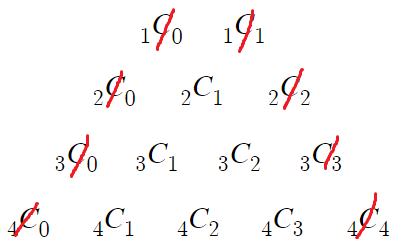
바깥쪽 1이라는건 빨갛게 표시한 부분 말하는거다
바깥쪽에 있는 부분의 값은 무조건 1이다.
그래서 말하고자 하는 바가 뭐냐면
하키스틱 법칙을 쓸거면 무조건 저 지점에서 시작해야한다.
그래서 이걸 어따가 써먹냐면
예를 들어 이런 문제가 나왔다고 해보자.
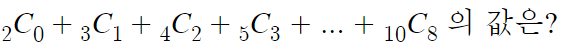
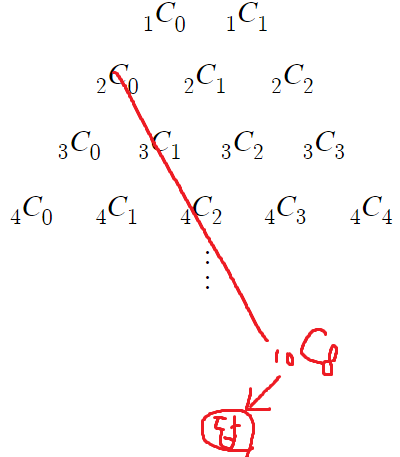
이런식으로 써먹을수 있다는것
바깥쪽 1에서 시작했고,
대각선 방향으로 내려왔으므로 하키스틱 법칙을 적용할수 있다.
그래서 답은 뭐냐면
저 답 위치에 있는건
파스칼 삼각형의 11번째 줄일거고
11번째 줄에서 8번째 항일 것이다.
따라서 답은

11 Combination 8 = 165 이다.
이 신기한 성질에 대한 증명은
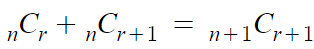
이걸 이용하면 할수 있지만
파스칼의 삼각형은 비중이 큰 부분이 아니기때문에 그냥 외워서 쓰자.
직접 해보는것도 나쁘지 않은 방법이다.
- 파스칼의 삼각형 예제 -
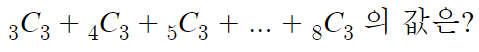
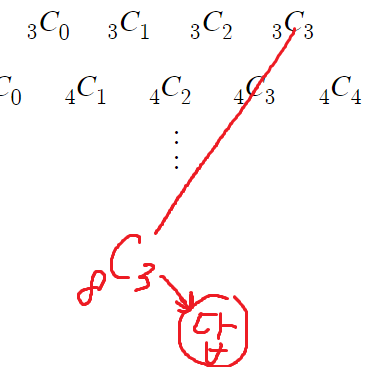
하키스틱 법칙을 이용하면
'답' 부분에 올것은
9번째줄의 4번째항
따라서 9C4 임을 알수 있다.
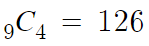
따라서 답은 126
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #1 - 이항정리의 뜻과 원리 (0) | 2021.11.29 |
|---|---|
| 중복조합 #2 - 중복조합을 이용한 경우의 수 (0) | 2021.11.27 |
| 중복조합 #1 - 중복조합의 뜻과 계산 원리 (1) | 2021.11.26 |
| 여러가지 순열 #3 - 같은 것이 있는 순열 (0) | 2021.11.26 |
| 여러가지 순열 #2 - 중복순열 (0) | 2021.11.24 |



