
그냥 쉽다.
- 중복순열 -
중복순열 : 중복을 허용하여 만든 순열
예를 들어, 숫자 1, 2, 3, 4, 5 중에서
중복을 허락하여 네 개를 택해 일렬로 나열하여 만들수 있는 수의
경우의 수를 구하라 한다면

숫자 5개고 자리 4개이다.
그리고 각 자리는 구별이 가능하다.

각각 천의 자리, 백의 자리, 십의 자리, 일의 자리 이기 때문이다.
즉 1이 천의 자리에 들어가는 경우와
1이 백의 자리에 들어가는 경우는 다른 경우이고 이를 구별해 취급해야한다.
여기서 핵심은
원래같았으면
숫자에게 자리 어디갈거냐고 물었을텐데
이런 상황에서 숫자에게 자리 어디갈거냐고 물어보면
1이 말하기를
난 천의자리도 가고싶고 백의자리도 가고싶다.
라고 해버려도 되는것이기 때문에
숫자에게 자리 어디갈거냐고 물을때는
자리 어디갈거고 몇자리 갈건지까지 물어봐야한다.
따라서 이건 상당히 비효율적인 방법이다.
예를 들자면 1111 이런수도 가능하기 때문이다.
따라서 이럴때는
반대로 자리에게 숫자 어떤거 원하냐고 물어봐야한다.
한 자리엔 한가지 숫자밖에 못오기 때문이다.
천의 자리에게 묻는다.
1,2,3,4,5 중 어떤 수가 왔으면 좋겠니?
그러면 천의 자리가 뽑을 수 있는 숫자는 1, 2, 3, 4, 5 중 하나이기 때문에
천의 자리가 숫자를 뽑는 경우의 수는 5
이번엔 백의 자리에게 묻는다.
어차피 중복해서 택하는게 허락되기 때문에
천의 자리가 무엇을 뽑았는지는 관심없다.
그냥 지 맘대로 1, 2, 3, 4, 5중에 하나 뽑으면 되는거다.
경우의수는 5
십의 자리도 똑같다.
앞의 두 자리가 뭘 뽑았는지는 관심없고 숫자 5개중 하나 뽑을거니까
경우의수는 5
같은 논리로 일의 자리가 숫자를 뽑는 경우의 수도 5이다.
즉 어차피 중복해서 뽑는게 허락되기 때문에
다른 자리들이 뭘 뽑았는지는 아무런 영향을 주지 않는다.
자리 입장에서는 그냥 주어진 숫자 5개중에서 하나를 뽑으면 되는거다.
따라서 숫자 1, 2, 3, 4, 5를 중복이 허락되게 나열하여
네자리 수를 만드는 경우는
천의 자리에 들어갈 숫자의 경우의 수
×
백의 자리에 들어갈 숫자의 경우의 수
×
십의 자리에 들어갈 숫자의 경우의 수
×
일의 자리에 들어갈 숫자의 경우의 수
=
5 × 5 × 5 × 5 = 5⁴
조금 난이도올린 예제 문제와 함께 정리해보자.

우선 네 자리의 자연수가 5의 배수려면
일의 자리가 0이거나 5여야 한다.
근데 주어진 숫자는 1, 2, 3, 4, 5 이니
일의 자리엔 5밖에 올수없다.
즉 일의자리에 1, 2, 3, 4, 5중 하나를 뽑아서 숫자를 배열하는 경우의 수는 1이다.
일의 자리만 5면 나머지 숫자가 무엇이든 어차피 5의 배수이므로
나머지 자리들은 1, 2, 3, 4, 5중에 중복 허락해서 아무거나 뽑으면 된다.
십의 자리에게 1, 2, 3, 4, 5중 하나 뽑으라 하면
5개중 하나 뽑는거니 경우의수 5
백의 자리에게 하나 뽑으라 하면
십의 자리가 뭐 뽑았는진 관심없고 5개중 하나 뽑는거니 경우의수 5
천의 자리에게 하나 뽑으라 하면
같은 논리로 경우의 수 5
따라서 구하고자 하는 경우의 수는 1×5×5×5 = 125
따라서 답은 3번이다.
- 일반화 -
서로 다른 5개에서 중복을 허용하여 4개를 택하는 경우의 수는
처음에 구했다시피
5 × 5 × 5 × 5 = 5⁴ 이다.
5개중 하나 선택하는 행위를 4번 하는 것이다.
따라서 일반화 해보자면
서로 다른 n개에서 중복을 허용하여 r개를 택하는 경우의 수는
n개중 하나 선택하는 행위를 r번 하는 것이므로
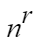
이렇게 되는거고
이를 표현하기를 이렇게 표현한다.
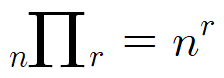
간단한 계산예제와 함께 마무리

5개중 하나를 뽑는 행위를 2번 한다.
즉 구하고자 하는 경우의 수는 5² = 25
따라서 답은 25
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #1 - 이항정리의 뜻과 원리 (0) | 2021.11.29 |
|---|---|
| 중복조합 #2 - 중복조합을 이용한 경우의 수 (0) | 2021.11.27 |
| 중복조합 #1 - 중복조합의 뜻과 계산 원리 (1) | 2021.11.26 |
| 여러가지 순열 #3 - 같은 것이 있는 순열 (0) | 2021.11.26 |
| 여러가지 순열 #1 - 원순열 (1) | 2021.11.23 |



