
확률과 통계 뿐만 아니라
고등학교 수학을 통틀어서 가장 쉬운곳이 통계이다.
난 평가원이 출제한 문제중 통계 문제는 틀려본적이 없다.
그만큼 쉽다.
다만 이 단원은 암기해야되는게 조금 있어서
처음 공부할때 그것만 좀 귀찮다.
- 통계학이란 무엇인가? -
무엇을 공부하는지는 알고 공부해야할거 아닌가?
통계학이란, 다량의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 학문이다.
고등수학 통계학에서 가장 많이 나오는 예가 점수이다.
A반엔 5명의 학생이 있는데,
각 학생의 시험점수가 60점, 70점, 80점, 90점, 100점 이라고 한다.
그리고 B반에도 5명의 학생이 있는데
얘네는 시험점수가 각각 20점, 30점, 40점, 50점, 60점 이라고 한다.
그러면 전체적으로 A반애들이 B반애들보다 점수가 높으니
A반이 B반보다 공부를 잘하는구나
이런식으로 '반 학생들의 점수' 라는 '데이터'를
'관찰'하고 '정리' 및 '분석'해서 A반이 B반보다 공부를 잘한다는 결론을 얻어냈다.
이런걸 하는게 통계학이다.
- 중등수학 복습 : 변량과 대푯값 -
아까 위로 들었던 예시에서
A반의 각 학생의 시험점수가 60점, 70점, 80점, 90점, 100점 이라 했는데
여기서 60점, 70점, 80점 하는 이 자료들이 각각 다 변량이다.
즉 여기서 변량 = 시험점수 인 것이다.
그리고 그 시험점수는 학생마다 다르므로 '변하는 값'이다.
그리고 아까 위로 들었던 예시에서
A반 학생들이 B반 학생들보다 공부를 잘한다는걸 어떻게 알았는가?
A반 학생들이 B반 학생들보다 점수가 높으니까
그 점수가 높다는건 또 어떻게 알았는가?
A반 학생들의 점수를 평균냈더니 80점이고
B반 학생들의 점수를 평균냈더니 40점이다.
따라서 평균적으로 A반 학생들이 B반 학생들보다 공부를 잘한다.
맞는 말이다.
여기서 핵심 키워드는 '평균'낸다음 비교했다는거다.
두 반의 점수 차이를 비교하기 위해
'평균값'을 구한것이다.
그리고 이 평균값은
A반은 80점
B반은 40점 이다.
즉 'A반 학생들의 시험점수' 라는 많은 자료를
대표할 수단으로 평균값을 채택한것이다.
즉 A반과 B반의 시험점수를 비교하려면
A반과 B반
각각의 시험점수를 대표할 값
즉 '대푯값'이 필요하다.
즉 대푯값 : 자료 전체의 중심적인 경향이나 특징을
대표적인 '하나'의 수로 나타낸 값
그리고 이 대푯값중 이번에 채택한게 '평균값' 이었던것이다.
대푯값의 종류는 여러가지가 있지만
고등수학 통계학에서는 평균만을 다룬다.
- 평균값의 한계와 산포도의 필요성 -
아까 반 학생들의 점수로 다시 예를 들자면
A반 학생은 4명이며
각 학생의 성적은 50점, 50점, 70점, 70점 이고
B반 학생은 4명이며
각 학생의 성적은 100점, 20점, 100점, 20점 이다.
A반과 B반 둘다 성적의 평균값은 60점 이다.
선생님이 A반과 B반에 수업들어가야 하는데
이 평균값이 60점이라는 정보만 가지고
딱 60점수준에 맞는 수업을 한다고 치자.
A반에서는 문제 없을것이다.
60점 수준으로 수업하면
50점인 학생들과 70점인 학생들이
수준 비슷하니까 따라와줄것이다.
근데 B반에서는 문제가 생긴다.
B반에서 60점 수준으로 수업하면
100점맞는 학생은 너무 쉬워서 재미없다며 딴짓하고
20점맞는 학생은 너무 어려워서 재미없다며 딴짓한다.
아무도 수업을 듣지 않을것이다.
평균값 하나만으로 분석하는것의 한계가 드러난것이다.
A반은 각 학생의 성적이
평균값인 60점에서 크게 벗어나지 않았기 때문에
평균값인 60점 수준으로 수업해도 큰 문제 없겠지만
B반은 각 학생의 성적이
평균값인 60점에서 크게 벗어나있기 때문에
평균값인 60점 수준으로 수업하면 문제가 생기는것이다.
따라서 데이터를 분석함에 있어서 다른 정보가 추가로 필요하다.
여기서 필요했던 추가정보는 무엇인가?
각 학생들의 성적이 평균값에서 얼마나 떨어져있었는지
즉 학생들의 성적의 편차가 어느정도인지를 알아야했다.
즉 학생들의 성적이 평균을 기준으로 얼마나 흩어져있는지를 추가정보로 알아야한다.
여기서 변량이 흩어져 있는 정도를 '산포도' 라고 한다.
여기서 산은 흩어질 산, 포는 펼 포
따라서 변량이 흩어지고 펴져있는 정도 : 산포도
그리고 산포도를 구하기 위해 알아야 하는 값이 편차
정도로 이해하면 된다.
그리고 잠깐 중등수학을 복습하고 넘어가자면
편차 = (변량) - (평균) 이다.
혹시 까먹고있었다면 알고 넘어가자.
그럼 산포도는 A반이 큰가 B반이 큰가?
B반이 크다. B반 학생들의 성적이 더 많이 흩어져있기 때문이다.
조금 고급지게 말하자면
B반 학생들의 성적의 편차가 더 크기 때문이다.
그리고 산포도도 대푯값처럼
종류가 여러가지 있는데
고등수학 통계학에서는 두개만 다룬다.
분산, 표준편차
여기까지 요약하자면
고등수학 통계학에서
대푯값은 평균
산포도는 분산, 표준편차
를 공부한다.
- 평균값 구하기 -
다시 성적을 예로 들자면
A반엔 5명의 학생이 있고
각 학생의 성적은 50점, 60점, 70점, 80점, 90점 이다.
A반 학생들의 성적의 평균은 70점이다.
혹시 평균 구하는방법을 까먹었다면

그리고 이건 중등수학이고
우리는 합을 나타내는 기호인 Σ를 배웠으니
이를 사용해서 평균을 다시 나타내보자.
우선 평균은 m 으로 표현한다.
mean이 의미하다 라는 뜻도 있지만 '평균'이라는 뜻도 있는데
여기서 따온거다.
그리고 변량의 개수를 n이라 하고
변량을 각각
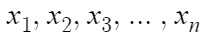
이런식으로 표현한다 해보자.
그러면 위의 평균 식을
다음과 같이 표현할 수 있다.
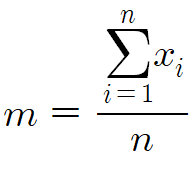
평균을 m으로 바꾸고
변량의 개수를 n으로 바꾸고
변량의 총합은 x₁+x₂+... 이니까
이걸 Σ로 표현한것이다.
조금 보기좋게 다시쓰면
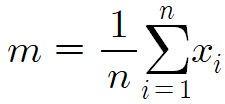
이 식은 알아두는게 좋다.
외우라는게 아니라
이 식을 보고 무슨 의미인지 해석할수 있으면 된다.
m은 평균
n은 변량의 개수
Σ어쩌고는 변량의 총합
- 산포도 중 하나인 분산 구하기 -
평균을 구했으니
이번엔 산포도를 구할 차례이다.
그중 분산을 구해볼것이다.
분산은 영어로 Variance라서 V라고 쓴다.
A반엔 5명의 학생이 있고
각 학생의 성적은 50점, 60점, 70점, 80점, 90점 이다.
A반 학생들의 성적의 평균은 70점이다.
그리고 산포도를 구하기 위해 필요했던
'편차' 를 각각 구해보자.
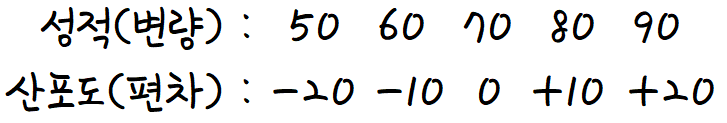
편차 = 변량-평균 이니까 각 변량에 대해 저렇게 될것이다.
평균값을 구할때는
변량의 총합을 변량의 개수로 나눠서 구했으니까
이번에 산포도 구할때도
편차의 총합을 편차의 개수로 나눠서 구해볼까?
즉 산포도로 편차의 평균을 구해보면 어떨까?
구해보면 0이다.
근데 여기서 문제가 있다.
편차의 평균은 무조건 0이기 때문이다.
왜냐면 편차 = 변량-평균 인데
평균을 이항하면 변량 = 편차+평균 이다.
근데 변량의 총합 / 변량의 개수 = 평균 이니까
(편차+평균)의 총합 / (편차+평균)의 개수 라고도 쓸 수 있다.
그리고 (편차+평균)의 총합 = 편차의 총합 + 평균의 총합
(편차+평균)의 개수 = 편차의 개수 = 변량의 개수
따라서 ( 편차의 총합 + 평균의 총합) / (편차+평균)의 개수 는
(편차의 총합 / 편차의 개수) + (평균의 총합 / 변량의 개수) 로 변환된다.

편차의 평균이 무조건 0이기 때문에
편차의 평균은 아무 쓸모가 없는 정보이다.
아무 통계나 가져와서 편차의 평균을 내면 전부 0이기 때문이다.
편차의 평균이 0이 되는 이유는 간단하다.
편차 = 변량-평균 인데
여기서 양수나온걸 다 그만큼의 음수가 상쇄시켜버리기 때문이다.
그래서 여기서 쓰이는 아이디어가
음수가 상쇄시켜버린다면, 음수를 전부 양수로 바꿔버리면 되지 않을까? 이다.
음수를 양수로 바꾸는 방법은
절댓값을 씌우거나, 제곱하거나 둘중 하나인데
여기서는 제곱하는 방법을 쓸것이다.
즉 편차의 제곱의 평균을 구해보자는거다.
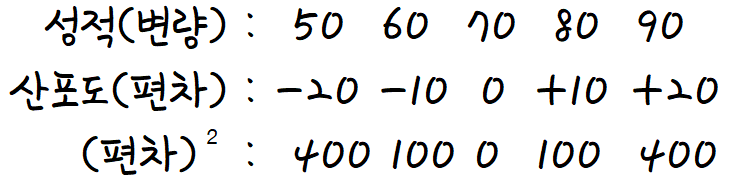
여기서 편차의 제곱의 평균을 구하면 200이다.
여기서 편차의 제곱의 평균을 '분산'이라 한다.
즉 여기서의 분산은 200인것이다.
이거는 어쩔수없이 암기해야한다.
위의 설명들은
아예 생으로 암기하면 영양가없으니
그럴싸한 이유를 만들어내는 과정이라 보면 된다.
- 산포도 중 하나인 표준편차 구하기 -
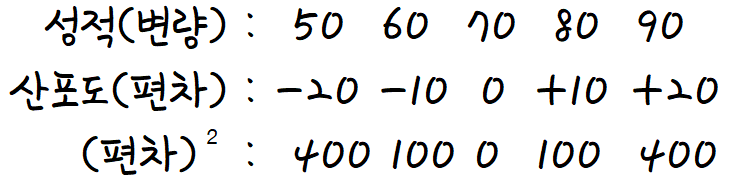
아까 여기서 분산이 200이라고 구했다.
근데 이 200이라는 값은
뭔가 변량, 편차 에 비해 커진 느낌이 있지 않은가?
그런 느낌을 받는 이유는
편차를 제곱한다음 평균냈기 때문이다.
제곱해버려서 크기가 커진것이다.
그럼 크기를 좀 안 커보이게 원상복구시키려면 간단하다.
제곱해서 이렇게된거니까 제곱근을 씌워버리면 된다.
즉 √(200) 을 구하겠다는것
여기서 √(200) 을 '표준편차' 라 한다.
즉 표준편차 = 분산의 양의 제곱근
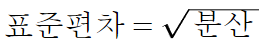
그리고 표준편차는 영어로 쓰면
standard deviation 이고
여기서 앞글자 s를 그리스 문자로 쓰면 σ 이다.
표준편차를 σ 라고 쓴다. '시그마'라고 읽는다.
이 내용도 어쩔수없이 암기해야한다.
뭔가 크기가 커진거같으니까 다시 제곱근을 씌우자는 얘기도
생으로 암기하면 영양가없으니까
그럴싸한 이유를 만들어낸것이다.
그리고 추가로, 표준편차가 분산의 양의 제곱근이니까
분산은 표준편차의 제곱이다.
따라서 분산을 σ² 이라 쓰기도 한다.
- 근데 표준편차를 이렇게 구하기는 번거롭다 -
제목 그대로다.
표준편차를 이렇게 구하려면
일단 평균을 구한다음
각 변량에 대한 편차를 구해서
그걸 제곱한다음 또 평균을 내고
그것의 제곱근을 구해야 비로소 표준편차가 나온다.
너무 불편하지 않은가?
방금건 변량의 수가 5개라 그나마 이정도로 끝났지
변량의 수가 1000개여도 이렇게 할건가?
너무 번거롭다. 식을 정리해서 간단하게 정리할 필요가 있다.
왜 번거롭냐면 계산 과정이 너무 길어서그렇다.
평균을 구하고
평균과 변량을 빼서 각각 편차를 구한다음
그 편차를 제곱하고
그 편차의 제곱을 평균낸다음
그것의 제곱근을 구해야한다.
이렇게 길어지는 계산과정의 근본적인 문제는
'편차를 구해야한다는 것'이다.
편차를 구하지 않고 표준편차를 구하는 방법을 알아볼것이다.
우선 표준편차 구하는 식은 그대로 쓴다.
표준편차는 분산의 양의 제곱근
분산은 편차의 제곱의 평균
근데 편차 = 변량-평균 이고
평균은 m
변량은 아래와 같이 나타낸다고 했다.
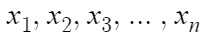
따라서 i번째 변량의 편차는
다음과 같이 쓸 수 있다.

그리고 편차의 제곱의 평균을 구해야하니까
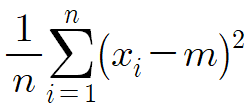
이걸 구해야한다.
이 식을 정리해볼것이다.
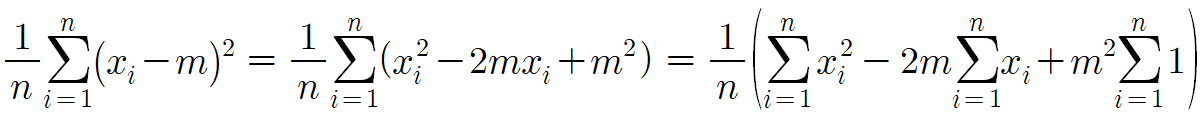
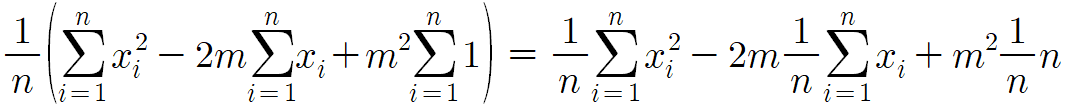
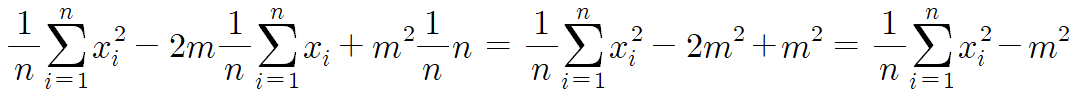
따라서 다음과 같은 결론을 얻는다.
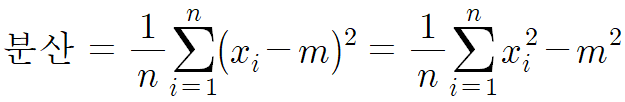
이를 말로 풀어주면
분산 = (변량을 제곱한것들의 평균) - (변량의 평균의 제곱)
표준편차는 이렇게 구한 분산에다가 제곱근만 씌워주면 된다.
이것도 사실상 암기해야한다.
그럼 이 식으로 위에 예로 들었던
A반 학생들의 성적 의 분산을 구해보자.
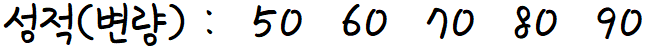
분산 = (변량을 제곱한것들의 평균) - (편량의 평균의 제곱)
변량을 제곱한것들의 평균은
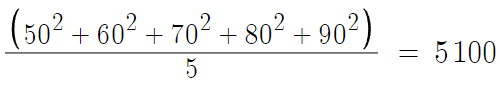
변량의 평균이 70이니까
변량의 평균의 제곱은 4900이다.
따라서 분산 = 5100 - 4900 = 200
표준편차 = √(200)
- 예제 -
5개의 변량 4, 10, x, y, 5의 평균이 6이고
분산이 4.4일 때, x²+y² 의 값은?
중등수학 쎈 교재에 있는 문제이다.
분산 = (변량을 제곱한것들의 평균) - (편량의 평균의 제곱)
따라서
4.4 = (변량을 제곱한것들의 평균) - 6²
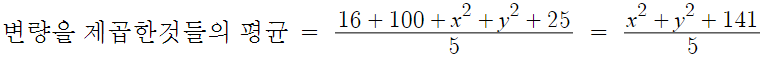
따라서 식을 정리하면

따라서 답은 61
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
|---|---|
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |
| 연속확률분포와 확률밀도함수 (0) | 2021.12.16 |
| 확률분포 #2 - 이항분포 (0) | 2021.12.14 |
| 확률분포 #1 - 이산확률분포 (0) | 2021.12.10 |



