
- 확률분포표 -
이산확률분포를 이해하려면
확률분포표에 대한 이해가 있어야한다.
또 시험점수로 예를 들자면
A반의 학생은 9명인데
각각 점수가 70점 80점 70점 50점 80점 80점 50점 70점 80점
이렇게 있다고 해보자.
A반 학생의 성적의 평균은?
70점 80점 70점 50점 80점 80점 50점 70점 80점
이걸 다 더한다음
A반의 학생수인 9로 나누면
70점이 나온다.
근데 이걸 더할때
좀 효율적으로 더하려면
70+80+70+50+80+80+50+70+80 이걸
그냥 생으로 더할게 아니라
70이 3개
80이 4개
50이 2개 있으니까
70×3 + 80×4 + 50×2 = 210 + 320 + 100 = 630
이렇게 더해야 효율적이다.
이걸 표로 나타내보자.
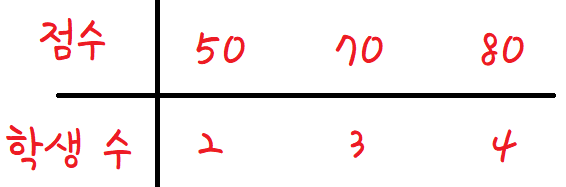
이렇게 될것이다.
여기서 변량은 학생의 시험점수
그리고 학생 수는 곧 이 변량의 빈도수이다.
그리고 이 변량을 X라 표현하고
빈도수에서 빈 빼서 도수라 표현하며
빈도수는 영어로 frequency
여기서 앞글자 f를 따서 f라고도 표현한다.
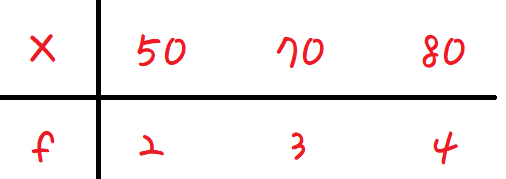
이처럼 각각의 변량과 도수에 대해 표로 나타낸것을
도수의 분포를 나타낸 표니까 '도수분포표' 라고 한다.
근데 우리가 알고싶은건 확률분포표 아닌가?
즉 각각의 변량과 확률에 대해 표로 나타낸것을 알고싶다는거다.
즉 도수를 확률로 바꿔야한다.
바꾸는 방법은 간단하다.
도수의 총합 = 변량의 총 수
따라서 각 도수를 도수의 총합으로 나눠주면
어떤 변량의 도수를 전체 도수로 나눈거니까
결론적으로 확률이 나오게 된다.

이를 다시 정리하면
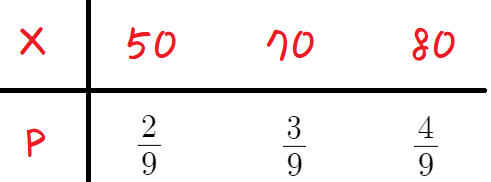
따라서
각각의 변량과 확률에 대해
위와 같이 표로 나타낸 것을
'확률분포표' 라고 한다.
그리고 X값에 따라 확률이 달라짐을 알수있다.
X값은 변량, 즉 변하는 값이며
이 값에 따라 확률이 정해지는것
따라서 여기서 X를 '확률변수' 라고 부른다.
- 이산확률분포표와 확률질량함수 -
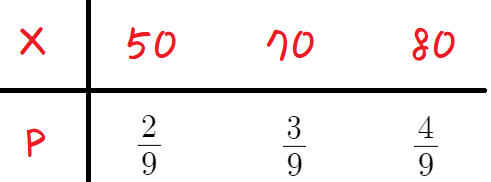
이 확률분포표를 보면
확률변수 X가
50, 70, 80 이니까
이 확률변수 X가 가질 수 있는값
즉 확률변수 X가 취할수 있는값은
3개이며 각각 50, 70, 80 이다.
즉 일일이 셀 수 있다.
이러한 확률변수를 '이산확률변수'라 한다.
그리고 이산확률변수와 확률에 대해
표로 나타낸것을 '이산확률분포표' 라고 한다.
처음에 예로 들었던게 이산확률분포 였던것이다.
그리고 여기서 P의 값은
확률변수 X에 따라 정해지는 값
즉 확률변수 X에 대해 대응되는 값이니까
P는 곧 확률변수 X에 대한 함수이다.
따라서 P(X)와 같이 나타낼 수 있으며
이를 '확률질량함수' 라 한다.
- 일반화 -
이산확률분포표를 일반화하면
아래와 같이 될것이다.
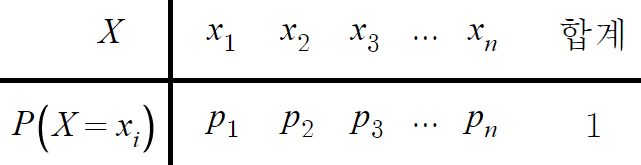
합계 1이 무슨말인지는 후술한다.
- 확률질량함수의 성질 -
1.
우선 확률질량함수라는건
일단 확률이니까
확률질량함수의 값은 0보다 크거나 같고, 1보다 작거나 같다.
즉 0보다 작아질수 없으며, 1보다 커질수도 없다.
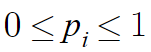
2.
이 확률질량함수의 값을 전부 더하면 어떻게될까?
아까 합계 1이 무슨말인지 후술하겠다 했는데
여기서 설명해주겠다는것
확률질량함수의 정의로 돌아가보자.
확률질량함수 P(X)는 곧 확률변수 X에 대한 값이다.
근데 이 확률변수 X라는건
거슬러 올라가보면 변량에서 온거다.
따라서 이 변량이 가질수 있는값
그 모든 값에 대한 확률질량함수의 총합을 구하면
결국 모든 경우의 확률의 총합이니까
1이 되는것이다.
즉 확률질량함수의 값을 전부 더하면 1이다.
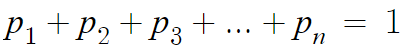
3.
이건 너무 당연한건데
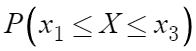
이것의 값은 무엇인가?
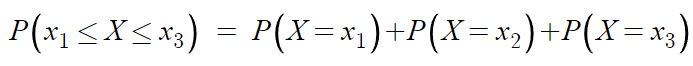
이거니까
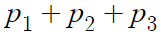
결국 이거 아닌가?
그럼 일반화를 위해
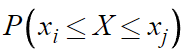
이것의 값은 무엇인가?
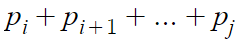
i번째 확률변수에 대한 확률질량함수부터
j번째 확률변수에 대한 확률질량함수까지 전부 더한 값이다.
따라서, 아래 식이 성립한다.
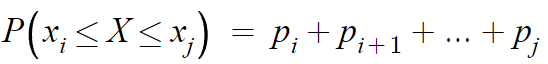
- 이산확률변수의 평균 -
우선 평균부터 구해보자.
확률변수 X의 평균을 E(X)라 쓰기로 '약속'한다.
E는 Expectation(기댓값) 에서 따온거라
평균을 기댓값 이라고도 한다.
그래서 E(X)의 값은 어떻게 구하냐면
맨 처음에 들었던 확률분포표 예시를 다시 가져오겠다.
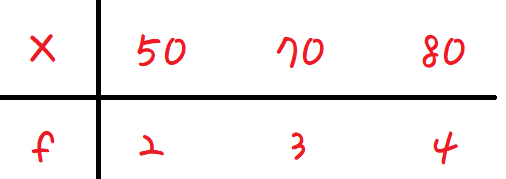
우선 이건 '도수분포표' 이다.
이것의 평균, 즉 E(X)는?
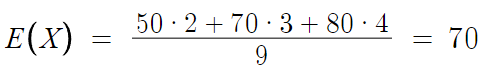
확률변수 X에 빈도수 f를 곱한다음 전부 더한다.
그다음 도수의 총합으로 나눈다.
근데 여기서 E(X)에서 9를
분배법칙 이용하면 이렇게 쓸수도 있을것이다.
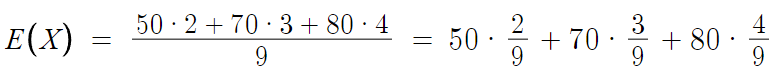
여기서 이것에 대한 확률분포표를 그대로 가져오겠다.
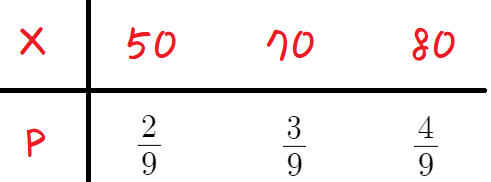
놀랍게도 각각의 확률변수 X에
그에 대한 확률밀도함수 P(X)를 곱한게
저 위의 E(X) 식에 그대로 들어가있다.
이건 우연이 아니다.
왜냐면 도수 f를 확률 P로 바꾸는 과정을 되새겨보면
P를 구하기 위해 도수 f에다 도수의 총합을 나누지 않았나?
즉 도수분포표에서 평균 E(X)를 구할때
다 더한 뒤 도수의 총합으로 나누는 계산과정은
확률분포표에서 평균 E(X)를 구할때
이미 확률 자체에 각각 도수의 총합이 나누어져 있기 때문에
이 도수의 총합으로 나눈다는 계산과정이 이미 되어있는것이다.
따라서 다음과 같은 결론을 얻는다.
확률분포표에서 평균(기댓값) E(X)를 구할때는
확률변수 X와 그에 대한 확률질량함수 P(X)를 곱한 뒤
전부 더해주기만 하면 된다.

이에 대한 예제로,
내가 즐겨하는 게임인 리그오브레전드에서
즐겨하는 챔피언인 트위스티드 페이트의 패시브스킬은 다음과 같다.
'유닛을 하나 처치할 때마다 주사위를 굴려 나온 눈의 수만큼의 골드를 랜덤하게 얻습니다.'
트위스티드 페이트가 유닛 1마리를 처치했을때
패시브스킬로 얻는 골드의 기댓값(평균)을 구해보자.
우선 유닛을 처치할때마다
주사위를 굴려 나온 눈의 수만큼의 골드를 얻는다고 했으니
얻는 골드는 1, 2, 3, 4, 5, 6 중 하나이다.
여기서 얻는 골드의 기댓값을 구하라 했으므로
얻는 골드를 확률변수 X라 한다면
E(X)를 구하라는 말이다.
우선 얻는 골드가 1, 2, 3, 4, 5, 6 총 6개로 일일이 셀수 있다.
따라서 X는 이산확률변수이다.
그리고 주사위를 굴려 나오는 눈은
1, 2, 3, 4, 5, 6 각각이 나올 확률이 같으므로
각각의 이산확률변수에 대한 확률질량함수의 값은 1/6 이다.
이를 토대로 이산확률분포표를 작성하면
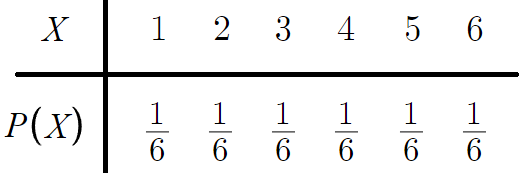
따라서 E(X)는
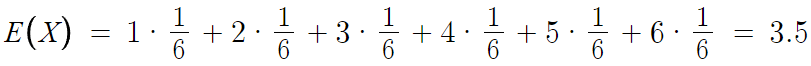
따라서 E(X) = 3.5이다.
트위스티드 페이트가 유닛을 처치할때마다
패시브스킬로 얻는 골드의 기댓값은 3.5이다.
- 이산확률변수의 분산과 표준편차 -
사실 이건 전의 글에서 설명해줬기때문에 이미 알고있다.
분산 = (변량의 제곱의 평균) - (변량의 평균의 제곱)
여기서 변량은 곧 확률변수 X니까
수식으로 바꿔쓰면
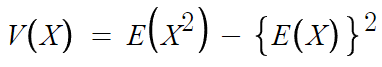
표준편차도 이미 알고있다.
표준편차 = 분산의 양의 제곱근
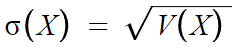
- 심화 : 확률변수 aX+b의 평균, 분산, 표준편차 -
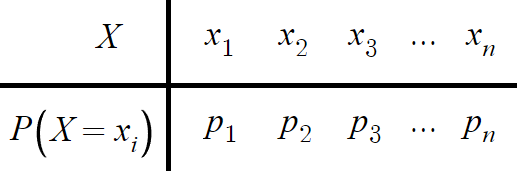
여기다가 그냥 확률변수 aX+b 를 대입하면 된다.
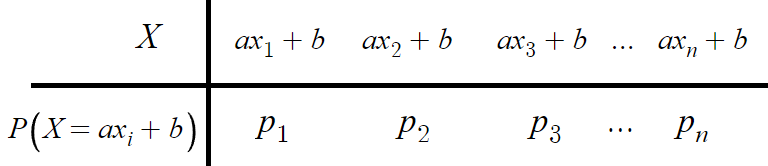
그다음 평균, 분산, 표준편차를 구해보자.
1. 평균
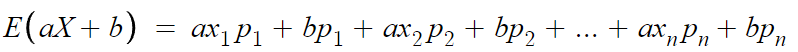
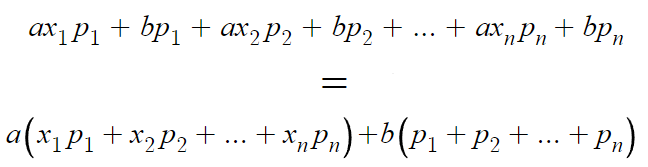
x₁p₁ + x₂p₂ + ... = E(X) 이고
p₁+p₂+... = 1 이므로
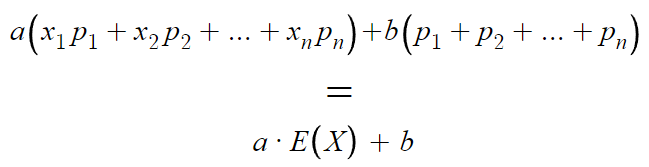
따라서 다음과 같은 결론을 얻는다.
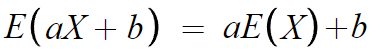
이 부분의 이해를 돕기 위해 첨언하자면
평균 이라는건 기댓값인데
모든 확률변수 X에 a라는 수를 전부 곱하면
당연히 평균적으로 확률변수의 값이 a배 될테니
평균값도 a배가 될것이다.
모든 확률변수 aX에 b라는 수를 전부 더하면
당연히 평균적으로 b라는 수를 더한게 되니까
aX의 평균값보다 b만큼 큰 평균값이 나오는거다.
2. 분산
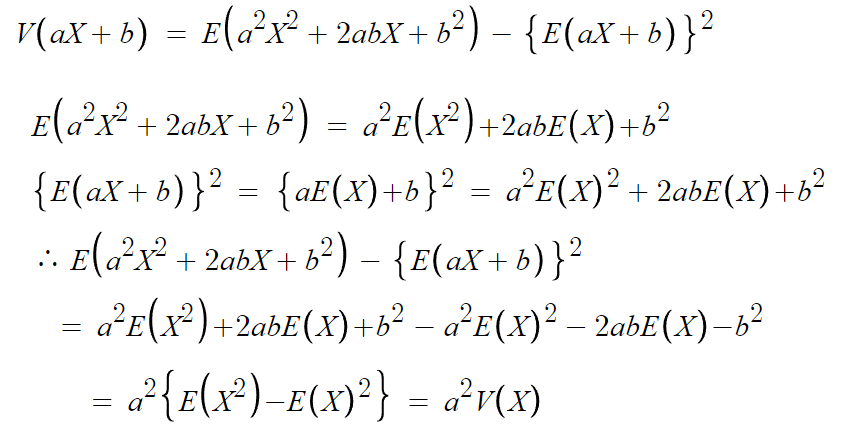
따라서 다음과 같은 결론을 얻는다.
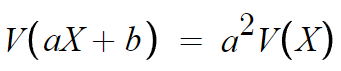
이해를 돕기 위해 첨언하자면
'분산'은 산포도이며
편차의 제곱의 평균이다.
따라서 확률변수 X에 a를 곱하면
편차도 각각 a배가 될거고
따라서 편차의 제곱은 a²배가 될것이다.
그리고 분산이 산포도기 때문에
확률변수 aX에 b를 더한다 한들
어차피 전부 b가 더해지는거라
퍼져있는 정도엔 아무런 영향을 주지 못한다.
그래서 b가 최종식에서 사라지는것이다.
3. 표준편차
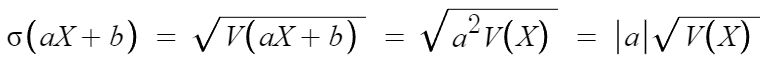
따라서 다음과 같은 결론을 얻는다.
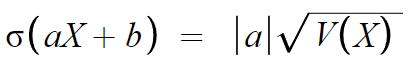
a에 절댓값이 들어가는 이유는 간단하다.
표준편차는 분산의 양의 제곱근이어야 하기 때문에
표준편차가 음수가 나오면 안된다.
근데 a가 음수일수도 있기때문에 a에 절댓값을 씌운것이다.
- 예제 -
1 )

확률분포표와 분산 값을 가지고
a와 b의 차이의 제곱 값을 구하는 문제이다.
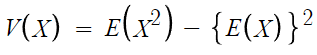
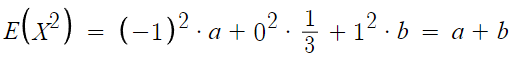
근데 확률질량함수의 두번째 성질에 의해
확률의 총합은 1이다.
문제에서는 친절히 합계 1이라고 표에 써놨지만
안써놔도 알아야한다.
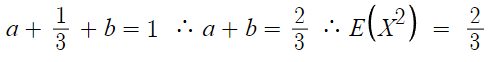
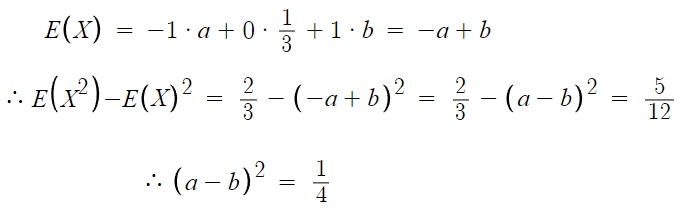
따라서 답은 4번
추가로, 미지수가 a,b로 2개고
관계식도 2개니 연립하면 a와 b를 구할수 있다.
a와 b를 각각 구해서 계산하는 방법으로 풀어도 되지만
하다보니 굳이 a와 b의 값을 구할필요는 없는 문제였다.
2 )
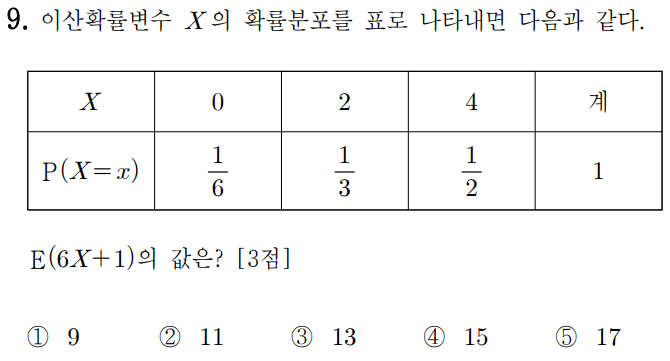
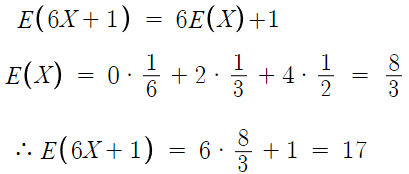
따라서 답은 5번
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
|---|---|
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |
| 연속확률분포와 확률밀도함수 (0) | 2021.12.16 |
| 확률분포 #2 - 이항분포 (0) | 2021.12.14 |
| 통계학 기초 - 기본 용어 (0) | 2021.12.09 |



