
- 연속확률분포와 연속확률변수 -
우리가 지금까지 한건 다 이산확률분포이다.
확률변수 X가 연속이 아니기 때문이다.
이산확률분포의 '이산'은 이산가족의 이산과 같은뜻이다.
서로 떨어져있다는 뜻이다.
즉 '이산'의 반대말은 '연속'이다.
근데 확률변수 X가 무조건 연속이 아닌걸까?
그니까 확률변수 X가 '연속'이면 어떻게 해야하느냐를 이번에 공부하는것이다.
예를 들어, 누군가에게 '키'가 몇이냐 물으면
대충 170cm라고 할텐데
그게 정확히 170cm인가?
170.3cm 일수도 있고
170.12398cm 일수도 있고
170.0001cm 일수도 있고
169.834832cm 일수도 있고
정확히 재기는 사실상 불가능한거 아닌가?
즉 '사람의 키' 라는 자료를
'정확히' 170cm라고 말할수 있는가?
당연히 아니다. 키가 몇이냐 물었을때 170cm라고 대답한건
대충 170cm '근처'니까 그렇게 대답한거다.
그럼 사람들에게 키가 몇이냐고 물어본다음
그 키를 확률변수 X로 해서 확률분포표를 작성해보자.

문제가 생겼다.
확률변수 X가 '이산'되어있는게 아니기때문에
표로 하나하나 적을수가 없다.
심지어 저건 키가 170.00015cm 이런사람도 있을테니 틀린 표이다.
따라서 이산확률분포표 작성하듯이
일일이 적어서 확률분포표를 작성하는건 불가능하다.
이런식으로 확률변수가 연속인걸
'연속확률변수' 라고 한다.
그럼 어떻게할까?
표를 작성하는게 안되니까
여기서 이용되는 아이디어는
표로 작성할수 없는이유가
확률변수 X가 연속이라 셀수없이 많기 때문이니까
확률변수 X를 하나하나 보지말고
확률변수 X의 '범위'로 나눠서 생각해보자는거다.
예를들어 '사람의 키' 라는 자료를 분석할때
150cm~160cm 인 사람
이런식으로 분석하자는거다.
직접 예로 들어보자.
사람 100명에게 키가 몇이냐고 물었다.
그리고 그 키를
150cm이상 160cm미만
160cm이상 170cm미만
170cm이상 180cm미만
180cm이상 190cm미만
이렇게 범위로 나누면
이제는 표로 정리가 가능하다.

도수 대신 확률을 넣어서
확률분포표로 만들려면
하던대로 하면 된다.
도수를 도수의 총합으로 나눈다.

- 확률밀도함수 -

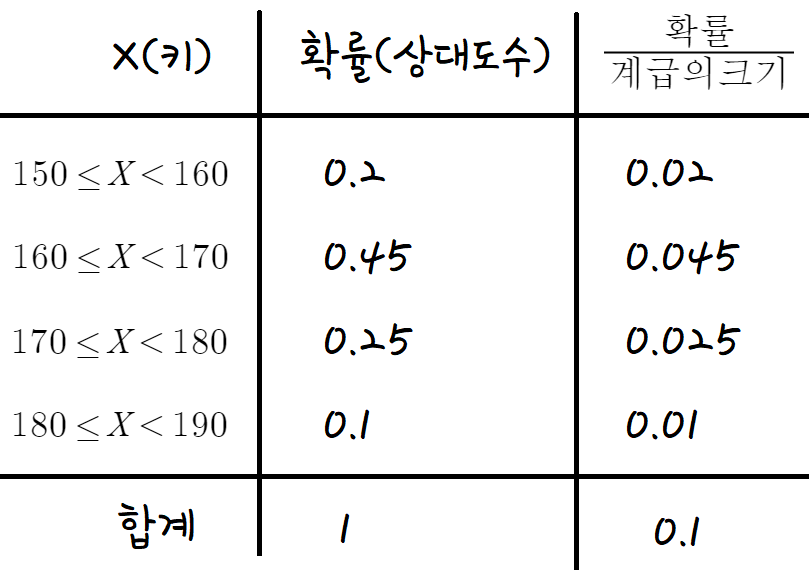
이 확률분포표에서 핵심은
확률분포표에서 각각의 확률을 모두 더하면 1 이라는것
확률분포표까지 만들었다.
이제 어떻게할거냐면
우선 사람의 키 라는 '변량'에서
각 구간의 계급의 크기는 얼마인가?
범위가 150~160, 160~170 이런식이니까
계급의 크기는 10이다.
이건 중등수학이다. 계급의 크기 = 구간의 길이
그래서 이제 어떻게할거냐면
확률을 계급의 크기로 나눌것이다.
이것도 아이디어 인데
일단 하다보면 이유를 알게된다.
그리고 이제 어떻게할거냐면
확률변수 X는 범위에 따라 나뉘어있고
이를 모두 표현하려면
표로는 불가능하다.
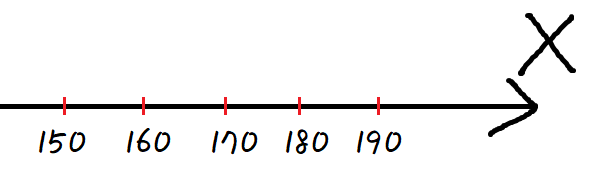
그래서 여기서 사용될게 바로 '그래프' 이다.
확률변수 X를 수직선에다가 나타내겠다는거다.
수직선엔 모든 실수가 들어가있기 때문이다.
그리고 이 확률변수 X에 대응되는
아까 구한 (확률)/(계급의크기) 값이 있다.
이것까지 표현하면
함수 y=f(x) 같은 느낌으로 표현될것이며,
'좌표평면' 에서의 '그래프'로 그려질것이다.
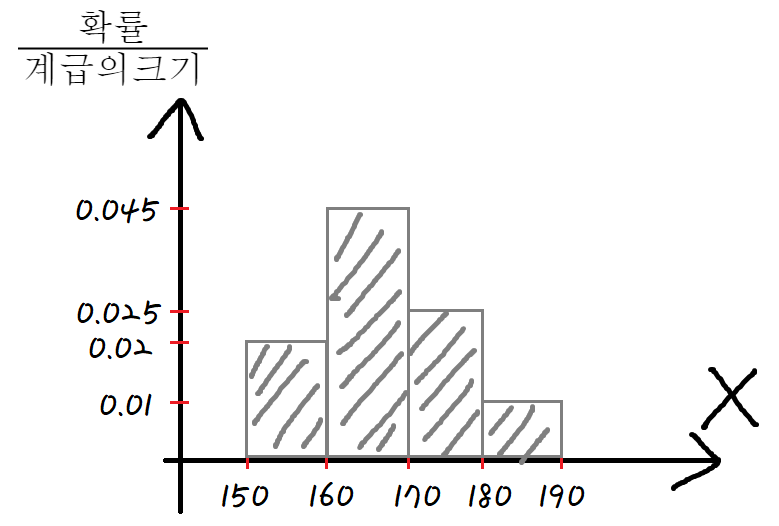
그래프로 나타내었다.
여기서 주목할건
저 구간별 직사각형의 '넓이' 이다.
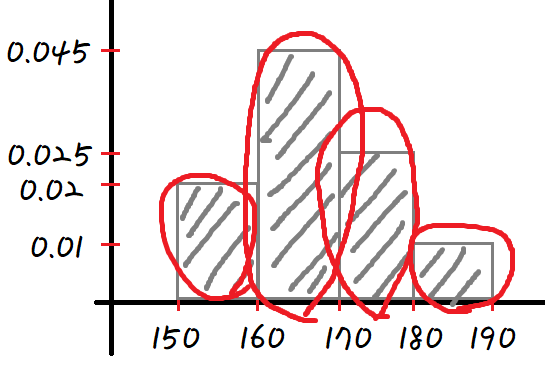
직사각형의 넓이는
(밑변) × (높이) 이다.
밑변은 무엇인가?
계급의 크기(구간의 길이)이다.
높이는 무엇인가?
(확률) / (계급의 크기) 이다.
따라서 직사각형의 넓이는

직사각형의 넓이가 확률이다.
아까 뜬금없이 확률을 계급의크기로 나눈 이유가 이것이다.
직사각형의 넓이가 확률이 되도록 하기 위해서이다.
근데 직사각형의 넓이가 왜 확률이 되어야할까?
확률의 총합이 1인것을 이용하기 위해서이다.
즉, 직사각형의 넓이의 총합은 1이다.
만약 이런 문제가 나왔다고 해보자.
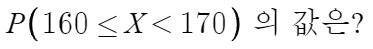
확률 = 직사각형의 넓이 이므로
답은 0.045 × 10 = '0.45'
즉 어떤 특정 구간의 확률을 구하라고 하면
그 특정 구간과 x축에 둘러싸인 부분의 넓이를 구하면 된다.
근데 여기서는 사람 100명이었는데
1000000명에게 물어본다면 어떻게될까?
그리고 구간을 10cm단위로 나누는게 아니라
1cm단위로 나누면 어떻게될까?
더 쪼개서 0.1cm단위로 나누면 어떻게될까?
'구간의 길이'가 줄어들면서 직사각형의 밑변의 길이도 줄어들것이다.
그럼 수많은 사람들이
'수많이 쪼개진' 구간중 하나에 들어가면서

이렇게 생겼던 그래프가
구간을 잘게 쪼개면 쪼갤수록 직사각형은 거의 선에 가까워질것이고
이것들을 전부 모은 그래프는
거의 '곡선에 가깝게' 될것이다.
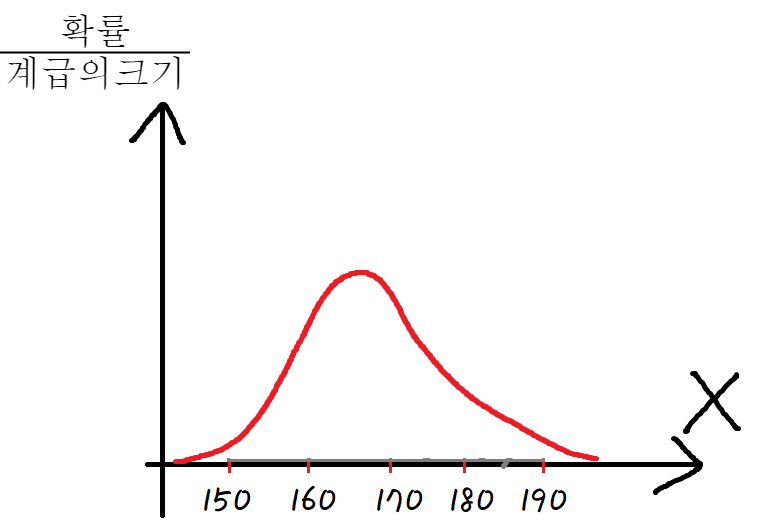
여기서 이렇게 얻어진 곡선을
'확률밀도함수' 라고 한다.
주의할건 꼭 곡선일 필요는 없다.
아까 직사각형 4개 나온 그래프도 확률밀도함수이다.
확률변수 X가 갖는 값에 대한 확률은
확률변수 X가 이산확률변수면 '확률질량함수' 인거고
연속확률변수면 '확률밀도함수'가 되는거다.
진짜 별거아니다. 확률을 나타내는 함수인것이다.
요약하자면
연속확률변수 X의 확률을 나타내는 그래프를 확률밀도함수라고 한다.
- 확률밀도함수의 성질 -
함수 f(x)가 연속확률변수 X의 확률밀도함수 라면
X는 확률밀도함수가 f(x)인 확률분포를 따른다. 라고 표현하고
아래 것들이 성립한다.
1.
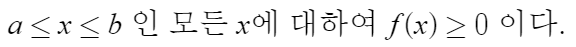
너무 당연한거다. f(x)가 확률을 나타내는 값이 되려면
확률은 음수일수 없기때문에 f(x)는 음수가 되면 안된다.
2.
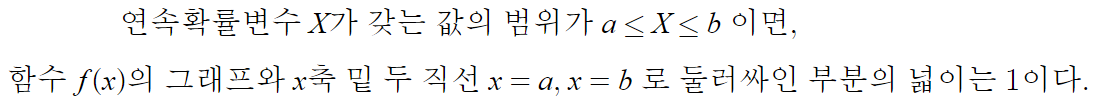
이것도 너무 당연한거고 여태 설명한거다.
그래프가 x축과 이루는 면적이 곧 확률이고
확률의 총합은 1이다.
저걸 좀 수학적으로 고급지게 정적분으로 표현하자면,
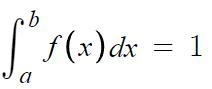
3.

이것도 너무 당연한것
확률 = 확률밀도함수가 x축과 이루는 넓이 이다.
a≤α≤β≤b 라는 조건은
그냥 α와 β가 a와 b 사이의 범위에서 벗어나면
연속확률변수 X가 갖는 값의 범위를 벗어나기때문이며
α≤β 라는 조건은 α>β면 P(α≤X≤β)=0 이기 때문에 있는것이다.
이것도 수학적으로 고급지게 표현하자면
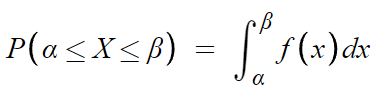
문제는 쉽게 나온다.
확률밀도함수가 뭔지,
확률밀도함수의 성질은 무엇인지
그정도만 알면 너무 쉽다.
어렵게 내봤자 정적분과 살짝 엮는정도인데
정적분의 값이 곧 확률을 나타낸다는걸 알고있다면 가소로울 뿐이다.
그리고 사실 여기서 어렵게낼 이유가 없다.
연속확률분포는 다음 내용인 정규분포가 본체이기 때문이다.
- 예제 -
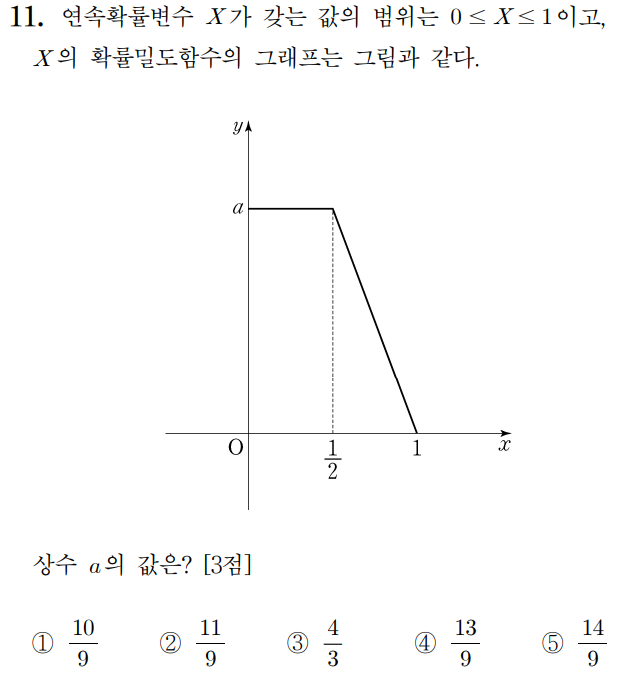
X는 연속확률변수이며
X가 갖는 값의 범위가 0≤X≤1 이며
X의 확률밀도함수의 그래프가 주어져있다.
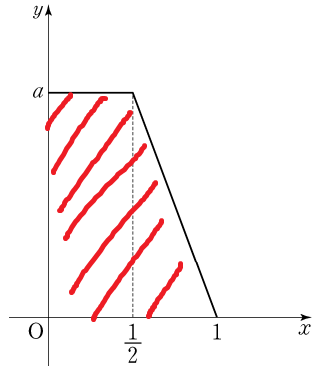
0≤X≤1 이므로 색칠한 부분은 X가 가질수 있는 모든 값에 대한 확률밀도함수의 넓이이고
이는 곧 확률의 총합을 의미한다.
따라서 색칠한부분의 넓이가 1임을 알수있다.
색칠한 부분의 넓이는
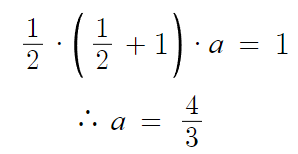
따라서 답은 3번
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
|---|---|
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |
| 확률분포 #2 - 이항분포 (0) | 2021.12.14 |
| 확률분포 #1 - 이산확률분포 (0) | 2021.12.10 |
| 통계학 기초 - 기본 용어 (0) | 2021.12.09 |



