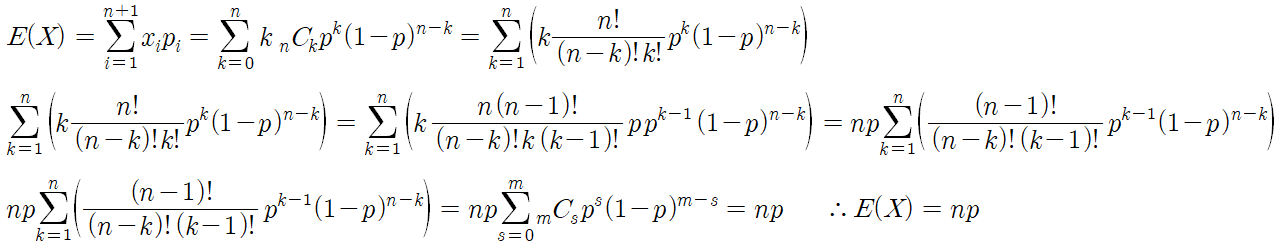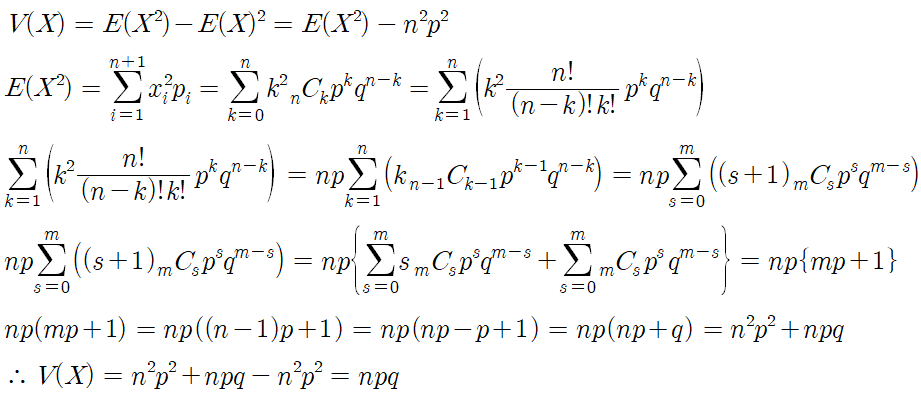- 이항분포 -
독립시행의 확률을 복습해보자.
주사위를 10번 던졌을때,
6의 눈이 3번 나올 확률은?
이 글은 독립시행의 확률을 구하는 글이 아니니까
그냥 답을 보여주겠다.
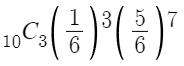
혹시 이것도 못구한다면
지금 통계 공부할때가 아니다. 독립시행의 확률부터 공부하고 오자.
근데 여기서 제시된 숫자중
가장 눈에 띄는것은 무엇인가?
6의 눈이 나오는 횟수인 '3' 아닌가?
그리고 이 나오는 '횟수'라는건
어떻게 보면 '변량' 아닌가?
그럼 이 횟수를 확률변수 X로 잡아버린다면?
주사위를 10번 던졌을때,
6의 눈이 나오는 횟수를 X라 하자.
그럼 이때의 확률분포표를 작성하면
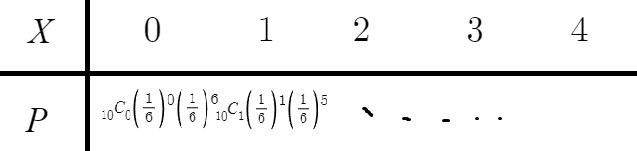
딱봐도 문제가 많다.
이걸 어느세월에 하나?
게다가 이걸 분석하려면
평균, 분산, 표준편차까지 구해야하는데
이걸 정말 하나하나 구할건가?
지금은 그나마 10번 던져서 이정도지
100번만 던져도 사실상 불가능해진다.
따라서 여기서도 아이디어가 필요하다.
그래서 여기서 쓰이는 아이디어는
저렇게 표를 작성할게 아니라
쉽게 구할수 있는 정보를 가지고 다르게 정리한뒤
'이항분포'라는 이름으로 내놓는것이다.
쉽게 구할수 있는 정보는
1. 시행횟수
2. 그 시행에서 특정 사건이 벌어질 확률
3. 그리고 각 시행이 독립시행임
그리고 사실 저 표를 작성하는데 이 정보 외에는 필요가 없다.
여기서 시행횟수는 10이고
특정 사건이라는건 6의 눈이 나오는거니까 확률은 1/6
그리고 독립시행이다.
따라서 시행횟수인 10과 확률인 1/6 만 가지고 이를 표현하는 방법이 있는데
그걸 이항분포라고 부른다는것이다.
이런 상황을 쓰기를

이렇게 쓴다.
왜 B라고 쓰냐면
Binomial Distribution : 이항 분포
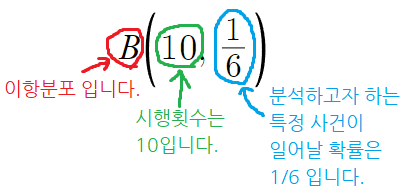
'일반화' 하자면
한번의 시행에서 특정한 사건이 일어날 확률이 p이고
그 시행을 n회 반복하며
각각의 시행이 독립시행일때,
특정한 사건이 일어나는 횟수를 확률변수로 하는 확률분포를
'이항분포' 라고 하며
아래와 같이 쓴다.

근데 왜 이름이 '이항'분포냐면
방정식 정리할때의 그 이항이 아니라
항이 두개라는 뜻의 이항이다.
이항정리와 같은 이항이다.
왜 항이 두개냐면
주사위를 굴릴때,
6의 눈이 나오는 경우
6의 눈이 나오지 않는 경우
이 두가지 경우만 취급하기 때문이다.
6이 나온게 아니라면
1이 나오는지 2가 나오는지는 관심이 없다.
어차피 우리가 원하는건 6이 나오는 횟수이기 때문이다.
그리고 통계에서 새로운걸 배웠으면
빠질수 없는게 평균, 분산, 표준편차 구하는거다.
- 이항분포의 평균(기댓값) -
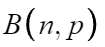
이것의 평균(기댓값)은 다음과 같다.

(시행 횟수) × (각 시행에서 사건이 일어날 확률)
이거는 그냥 암기하면 된다.
암기하기도 쉽다.
일어날 확률 1/4 인데 40번 시행하면
확률이 1/4니까 10번쯤 일어날거같은 감이 오지 않는가?
엄밀한 증명은 고등학교 과정에서 다루지 않는다.
하지만 증명은 고등수학수준 내용으로 가능하기 때문에
보여주긴 할건데 안봐도 된다. 궁금하면 보자.
- 이항분포의 분산 -
분산도 암기해야한다.
E(X²) 의 평균을 증명하는것도 고등학교 과정에서 다루지 않기 때문이다.
q = 1-p 라고 하면

(시행 횟수) × (각 시행에서 사건이 일어날 확률) × (일어나지 않을 확률)
이것도 증명 과정이 궁금하면 보여줄건데 안봐도 된다.
- 이항분포의 표준편차 -
표준편차 = 분산의 양의 제곱근
따라서 이항분포의 표준편차는 다음과 같다.

- 예제 -
1 )

E(X) = np
n = 12, p = 1/3 이므로
계산하면 E(X) = 4
따라서 답은 4번
2 )

동전 2개를 동시에 던지는것이므로
두 동전은 각각 독립시행이고
동전을 2개 던진다는 각 시행마다도 독립시행이다.
독립시행에서의 특정 사건이 일어나는 횟수를 확률변수 X로 두고 있으므로
이것은 확률분포 중에서도 이항분포 문제임을 알 수 있다.
V(4X+1) = 16V(X)
V(X) = npq
n과 p만 찾으면 된다.
n은 시행횟수이다.
동전 2개를 동시에 던지는 시행을 10회 반복한다고 했으므로
n=10 이다.
그리고 동전 2개 모두 앞면이 나오는 횟수를 확률변수 X로 두고 있으므로
p = 동전 2개 모두 앞면이 나올 확률
따라서 p = 1/4
따라서 이것의 이항분포는 B( 10, 1/4 ) 로 표현할수 있고
q = 1 - 1/4 = 3/4 이므로
V(X) = 10 × 1/4 × 3/4 = 30/16
따라서 16V(X) = 30
따라서 답은 30
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
|---|---|
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |
| 연속확률분포와 확률밀도함수 (0) | 2021.12.16 |
| 확률분포 #1 - 이산확률분포 (0) | 2021.12.10 |
| 통계학 기초 - 기본 용어 (0) | 2021.12.09 |