
이거까지 마치면
이차방정식의 근에 관련해서는
거의 다 했다고 볼수 있다.
결론은 뭔가 무시무시하게 생겼지만 너무 당연한데서 나온거라서
이전의 내용을 잘 따라왔다면 금방 이해할수 있다.
- 개요 -
이번엔 뭘 할거냐면

이런문제를 풀어볼것이다.
뭐 어쩌라는건지 모를텐데 답은 아주 간단하다.
한 근이 1-2i 니까 다른 한 근은 1+2i 이다.
설명은 차근차근 하겠다.
- 왜? -

왜 답이 1+2i 인가?
이것의 해답은 '근의공식'에 있다.
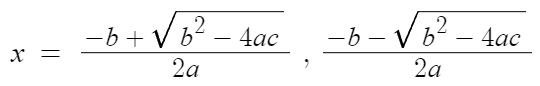
잘 보면
두 근의 값에서 다른점이 하나밖에 없다.

이 부분의 부호 빼고 전부 똑같다.
근데 한 근이 1-2i 라고 한다.
허수단위 i가 등장할만한 곳은
저 루트부분밖에 없다.
따라서 저 루트부분의 값이 2i임을 알수 있고,
근의 공식에 의하면
루트 앞의 부호만 바꾸면 다른 한 근이 되는거니까
1-2i 에서 2i 앞의 부호만 바꾸면
1+2i 가 다른 한 근이라는 결론을 낼 수 있다.
왜 이번 주제 이름이 켤레근인지 감이 오나?
2+3i 의 켤레복소수가 2-3i 인것과 같이
이차방정식의 근에서도
켤레 관계를 찾을수 있기 때문이다.
- 연습 -

우선 이차항의 계수는 1로 실수
일차항의 계수도 a로 실수
상수항도 b로 실수 이므로
3+4i 의 켤레근은 3-4i 이다.
따라서 두 근은
3+4i 와 3-4i 이다.
근데 여기서 질문이 있을수 있다.
왜 계수가 실수여야 하나요?
계수가 허수면
근의공식을 적용했을때 허수단위 i가
루트가 아니라 다른곳에서 등장할수도 있다.
그러면 다른 한 근이 3-4i 라고 보장할수 없다.
그래서 실수라는 조건이 들어가야 하는것이다.
아무튼 두 근을 알아냈다.
3+4i 와 3-4i 이다.
근과 계수의 관계를 이용하면
a = - (두 근의 합)
b = (두 근의 곱)
따라서 a=-( 3+4i + 3-4i ), b=3²-(4i)² 이다.
따라서 답은 a=-6, b=25
- 일반화 -
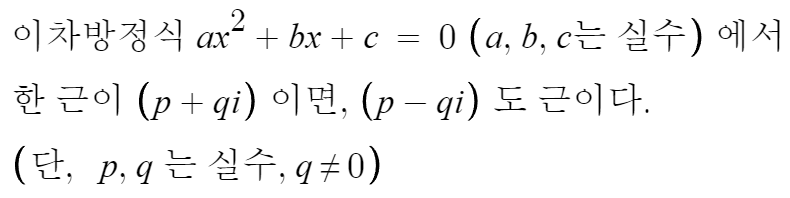
계수가 모두 실수면
여기서 허수단위 i가 등장할 곳이
근의공식에서 '루트부분'밖에 없으므로
한 근을 알고있으면
거기서 허수부분의 부호만 바꿔주면
그것도 근이다.
이걸 '켤레근' 이라 한다.
추가로, p,q가 왜 실수여야 하냐면
p, q가 허수면 p+qi 에서
어디가 실수부분이고 허수부분인지 모르게되기 때문이다.
q≠0 이어야하는 이유는
q=0이면 허수부분이 0이라서 켤레근이 존재하지 않는다.
정확히는 x=p 라는 중근을 갖는다.
- 근이 허수가 아니어도 가능 -
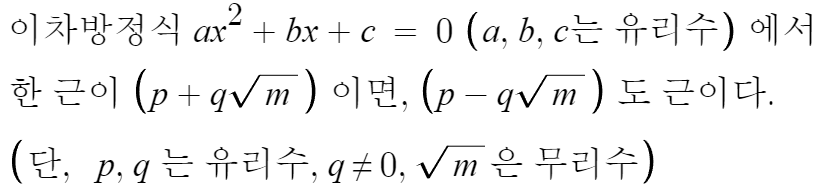
바뀐건 하나밖에 없다.
계수가 실수가 아니라
계수가 '유리수'여야한다.
아까와 논리는 똑같다.
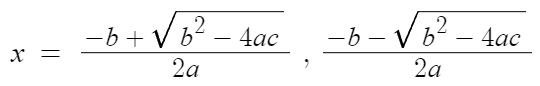
유리수인 계수들을 가지고 근의공식을 써서
결과값으로 무리수인 (√m) 이 등장하려면
루트부분이 무리수인 수밖에 없고
따라서 무리수부분의 부호만 바꿔주면 다른 근을 얻게되는거고
그걸 켤레근이라 한다.
그리고 계수가 유리수여야 하는 이유도 같은 논리이다.
계수가 무리수면 근의공식을 썼을때 어디서 무리수가 등장하는지 알수 없다.
- 예제 -
1 )
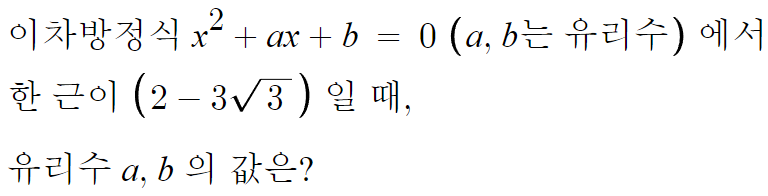
이차항의 계수, 일차항의 계수, 상수항 모두 유리수이기 때문에
켤레근을 적용할수 있다.
( 2 - 3√3 ) 이 한 근이면
루트 앞부분의 부호만 바꾼
( 2 + 3√3 ) 도 근이다.
이제 a, b의 값을 구하기 위해
근과 계수의 관계를 이용하면
a = - (두 근의 합)
b = (두 근의 곱)
따라서 a = - ( 2-3√3 + 2+3√3 ) = -4
b = ( 2 - 3√3 )( 2 + 3√3 ) = 4-27 = -23
따라서 답은 a=-4, b=-23
2 )

혹시 답이 4+2√3 이라고 나왔나?
틀렸다. 문제를 다시 읽고 다시 풀어보자.
개념공부 대충한사람 낚으려고 일부러 이런 문제로 뽑았다.
쓸데없이 이상한문제 가져왔다고 불평할수 있는데
교육청 모의고사 기출문제인데 불만있나?
- 제대로 된 풀이 -
답이 4+2√3 이라고 나왔다는건
한 근이 2+√3 이니까
다른 한 근은 켤레근인 2-√3 이겠네
하고 풀어서 그런거다.
결론부터 말하자면 거기부터 잘못되었다.
왜 잘못되었느냐?
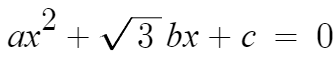
일차항의 계수가 (√3 × b) 이다.
b는 유리수이기때문에 (√3 × b) 는 무리수이다.
계수가 무리수이면 켤레근 풀이를 적용할수 없다.
아까 설명했던 내용이다.
계수가 무리수이면
근의 공식을 적용했을 때,
근에서 무리수 부분이 정확히 루트부분에서 나왔다는 보장이 없기 때문이다.
그래서 켤레근 2-√3 도 근이라고 풀면 안되고
근의공식을 직접 써서 구해야한다.
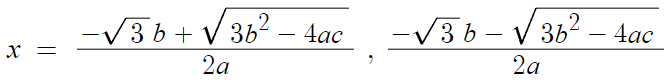
이것에 따르면
2+√3 이 근으로 나오려면
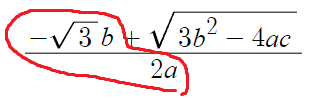
표시한 부분이 '무리수' 이므로 이 부분이 √3 이고
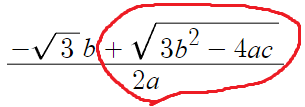
따라서 여기서 표시한 부분의 값은 2가 나와야 한다.
따라서 두가지 관계식을 얻을수 있다.
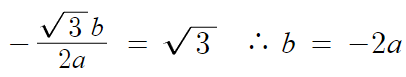

b=-2a, c=-a 이므로
a, b, c를 a라는 문자 하나로 통일하여 표현할 수 있다.
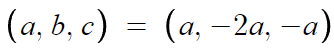
이걸 문제에서 제시한 이차방정식에 대입하여 정리하면
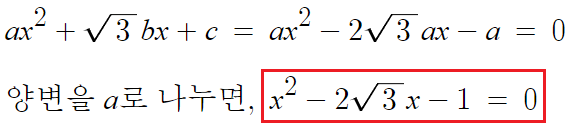
문제가 참 아름답게도 이차방정식 자체를 알아내버렸다.
이제는 쉽다. 근의공식만 써주면 β의 값을 알수 있을거고
그대로 계산만 하면 된다.
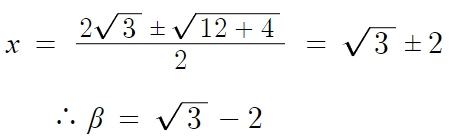
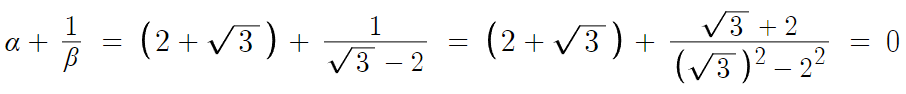
따라서 답은 0이다.
'수학(상) > II. 방정식' 카테고리의 다른 글
| 이차함수 #2 - 이차함수의 그래프와 직선의 위치 관계 (0) | 2022.01.26 |
|---|---|
| 이차함수 #1 - 이차방정식과 이차함수의 관계 (0) | 2022.01.25 |
| 이차방정식 #4 - 이차식의 인수분해 (0) | 2022.01.21 |
| 이차방정식 #3 - 근과 계수의 관계 (0) | 2022.01.16 |
| 이차방정식 #2 - 근의 판별 (0) | 2022.01.16 |



