
- 개요 -
우선 근과 계수의 관계라는게 무슨말인가?

이차항의 계수 : a
일차항의 계수 : b
상수항 : c
인 이차방정식이다.
이 이차방정식의 계수인 a, b, c 와
이 이차방정식의 근이 특별한 관계가 있다.
이번에 다룰것은
1. 두 근의 합
2. 두 근의 곱
이 두가지이다.
이 두가지와 계수가 특별한 관계가 있다는것이다.
- 근과 계수의 관계 1 : 두 근의 합 -
어떤 특별한 관계가 있냐면
일단 근의 공식을 써보자.

따라서 근은 다음과 같다.

근데 아까 '두 근의 합, 곱'과 관계가 있다했는데
여기서 두 근의 합을 구해볼까?

두 근의 합은 이렇게 될것이고

위처럼 √(b²-4ac) 가 계산되면서 0이 될것이다.
따라서 두 근의 합은 아래와 같이 된다.
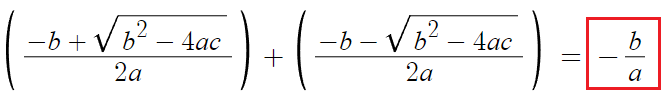
두 근을 직접 구하지 않아도
계수만 가지고 두 근의 합을 구할 수 있다.
결론내자면, 아래와 같다.

- 근과 계수의 관계 2 : 두 근의 곱 -
똑같이 근의 공식을 써보자.

그다음 두 근을 곱해보자.
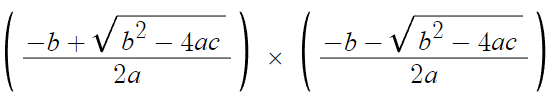
이걸 구하는것이다.
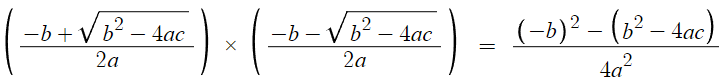
합차공식을 이용하면 위와 같이 되고
정리하면, 결론은

두 근을 직접 구하지 않아도
계수만 가지고 두 근의 곱을 구할 수 있다.
결론내자면, 아래와 같다.

- 심화 : x²의 계수가 1일때 -

우선 이 식에서
x²의 계수를 1로 만들기 위해
양변에 a를 나눠주면
아래와 같이 될것이다.

갑자기 x²의 계수를 왜 1로 만들었냐면

방금전에 공부했던 모양이 그대로 나왔다.


따라서

이 식은 아래와 같이 표현할 수 있다.

여기서 두 근을 각각 α, β 라고 하면
아래와 같이 표현할 수 있게된다.
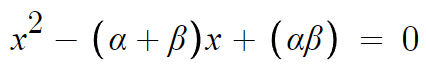
α, β같이 이상하게생긴 문자가 등장했다고 겁먹지 말자.
그냥 '이 방정식은 두개의 근을 가질텐데
그 근을 문자로 표현해야되니까
두 근중 하나는 α라 쓰고 나머지 하나는 β라고 쓰자.'
라고 한것뿐이다.
따라서 일반화하자면,
두 수 α, β를 근으로 하고
x²의 계수가 1인 이차방정식은
아래와 같이 표현할 수 있다.

- 예제 -
1 )


여기서 a=1, b=-1 인 것이다.
따라서 두 근의 합은
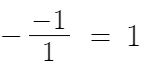
따라서 답은 1
이차항의 계수가 1이니까
아까 심화부분의 내용을 가지고 풀어도 된다.

α+β가 두 근의 합인데
-(α+β) = -1 이어야 하므로
α+β=1 이고 따라서 답은 1이다.
2 )


여기서 a=1, c=2 인 것이다.
따라서 두 근의 곱은

따라서 답은 2
이차항의 계수가 1이니까
아까 심화부분의 내용을 가지고 풀어도 된다.

αβ가 두 근의 곱인데
αβ=2 이어야 하므로
αβ=2 이고 따라서 답은 2이다.
3 )

우선 주어진대로 이차방정식을 써보자.

여기서 a=3 이다.

b와 c의 값을 알아내면 되는데
두 근이 주어져있으니
근과 계수의 관계를 이용해볼수 있겠다.
두 근의 합 = -1/3 + 1 = 2/3

따라서 b=-2

이제 c만 구하면 된다.
두 근의 곱 = (-1/3)×1 = -1/3

따라서 c=-1 이고
이차방정식을 완성시킬수있다.

따라서 답은 3x²-2x-1=0
'수학(상) > II. 방정식' 카테고리의 다른 글
| 이차방정식 #5 - 이차방정식의 켤레근 (0) | 2022.01.22 |
|---|---|
| 이차방정식 #4 - 이차식의 인수분해 (0) | 2022.01.21 |
| 이차방정식 #2 - 근의 판별 (0) | 2022.01.16 |
| 이차방정식 #1 - 이차방정식의 풀이 (0) | 2022.01.14 |
| 복소수 #3 - 복소수의 사칙연산, 음수의 제곱근 (0) | 2022.01.14 |



