
- 복소수의 사칙연산 -
아주 간단하다.
복소수도 다항식처럼
교환법칙, 결합법칙, 분배법칙이 성립한다.
따라서 다항식의 사칙연산 하듯이
그냥 똑같이 하면 된다.
사칙연산이 동류항끼리 모아서 계산하듯이
복소수는 실수부분끼리, 허수부분끼리 모아서 계산한다.
곱셈은 분배법칙을 이용해 계산한다.
직접 해보자. 정말 쉽다.
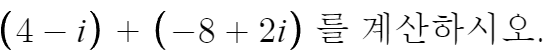
4-i의 실수부분은 4
허수부분은 -1
-8+2i의 실수부분은 -8
허수부분은 2
이걸 덧셈연산하라니까
실수부분은 (4)+(-8) = -4
허수부분은 (-1)+(2) = 1
따라서 답은
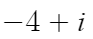

하던대로 분배법칙으로 계산한다.
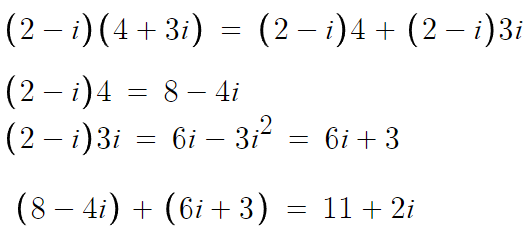
따라서 답은 11+2i
- 복소수의 나눗셈 -
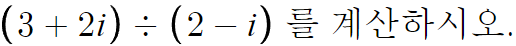
이건 그냥 계산하면 문제가 생긴다.
2-i 는 실수가 아니기때문이다.
위 문제는 곧
이걸 구하라는 말인데
분모가 실수가 아니기때문에
분모를 실수로 만들어줘야한다.
즉 '분모의 실수화' 를 해줘야한다.
분모의 실수화 하는 방법은

일단 이거 복습겸 해서 풀어보자.
저건 '분모의 유리화' 를 해준뒤 푼다.
√(3)을 없애기 위해
분모분자에 1-√(3) 을 곱해주면
합차공식에 의해 √(3)이 소거되고
따라서 분모가 유리수가 되어서
계산할수 있게된다.
이것도 똑같이 하면 된다.
합차공식을 적용해서 i를 없애버리는거다.

따라서 답은
- 예제로 중간점검 -
1 )
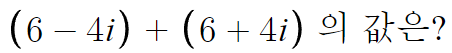
실수부분끼리 모아서,
허수부분끼리 모아서 계산한다.
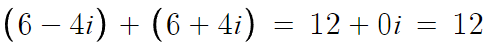
따라서 답은 12
2 )

복소수의 나눗셈연산중 '분모에 허수가 있는 경우' 엔
분모를 실수로 바꿔준다.
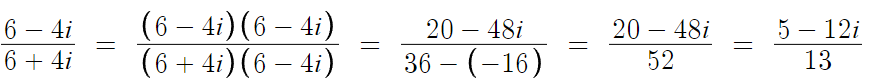
따라서 답은
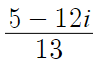
- 음수의 제곱근 -
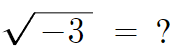
우리가 음수의 제곱근을 여태 다루지 못했던 이유는
'허수'라는것의 존재 자체를 안배웠기 때문이다.
이젠 배워서 다룰수 있다.
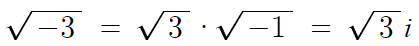
음수의 제곱근은 이렇게 허수단위 i로 나타낼 수 있다.
따라서 -3의 제곱근은
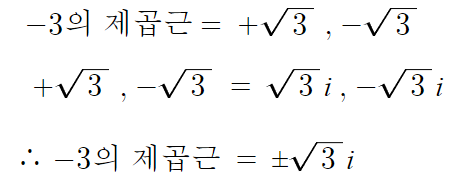
따라서 다음과 같이 일반화 할 수 있다.
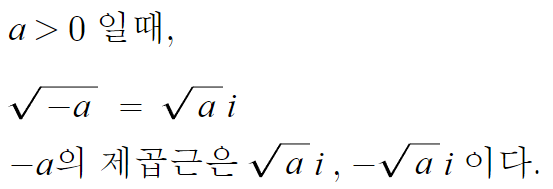
- 음수의 제곱근의 성질 -
허수단위 i때문에
음수의 제곱근을 다루다보면
신기한 일이 벌어진다.
1 )
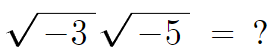
이건 어떻게 나타낼수 있을까?
√(15) 일까?
직접 구해보자.
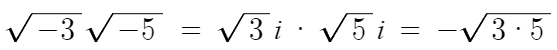
따라서 다음과 같이 일반화 할수 있다.
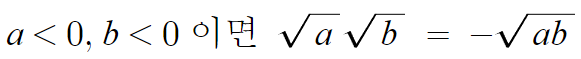
a와 b에 둘다 마이너스가 붙었으니
이때는 루트 안의 것을 단순히 곱한것을 결과로 내놓는게 아니라
마이너스를 붙여줘야한다.
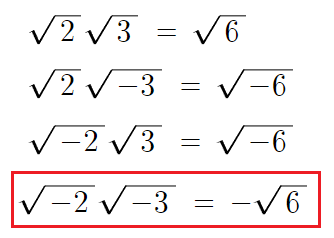
2 )
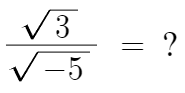
이건 어떻게 나타낼수 있을까?
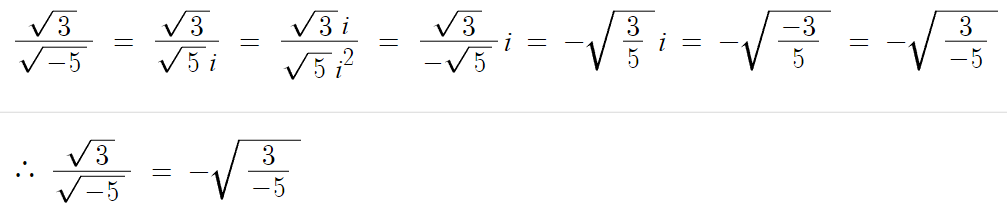
즉 분자의 루트 안에 있는것만 음수인 경우엔
마이너스가 생겨줘야한다.
왜 얘만 마이너스가 생기는가?
분모만 허수인건 이 경우밖에 없기 때문이다.
분모가 허수라서 계산을 위해 분모의 실수화를 하다보니 저렇게 된것이다.
따라서 다음과 같이 일반화 할수 있다.
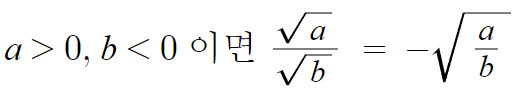
분모만 허수인 경우엔
루트 안의 것을 단순히 나눈것을 결과로 내놓는게 아니라
분모의 실수화를 하다보면 마이너스가 나오게된다.
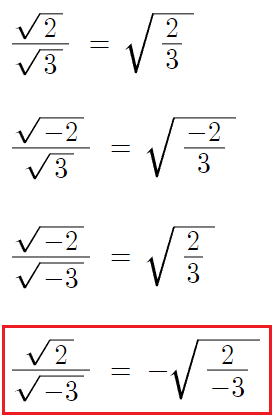
- 예제 -
1 )

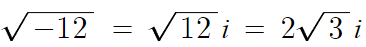
따라서 답은 2√(3)i
2 )
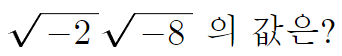
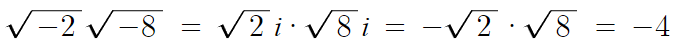
따라서 답은 -4
3 )

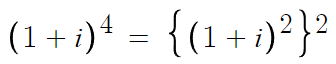
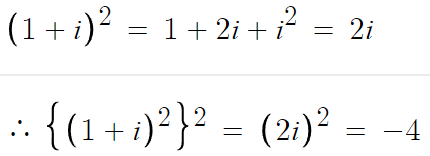
따라서 답은 -4
4 )
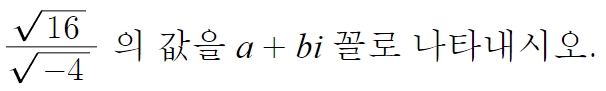
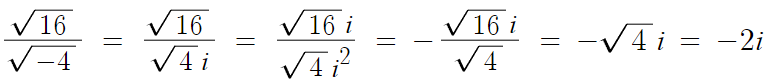
따라서 답은 -2i
'수학(상) > II. 방정식' 카테고리의 다른 글
| 이차방정식 #3 - 근과 계수의 관계 (0) | 2022.01.16 |
|---|---|
| 이차방정식 #2 - 근의 판별 (0) | 2022.01.16 |
| 이차방정식 #1 - 이차방정식의 풀이 (0) | 2022.01.14 |
| 복소수 #2 - 복소수의 뜻과 켤레복소수 (0) | 2022.01.11 |
| 복소수 #1 - 허수란 무엇인가? (0) | 2022.01.10 |



