
- 근의 판별이란? -
우선 이차방정식은 두 개의 근을 갖는다.
근데 이 근이 실근인지, 허근인지 를 구별하는게 근의 판별이다.
이차방정식은 근이 두개니까
실근 두개, 허근 두개, 실근하나 허근하나
이 셋중 하나일것이다.
근데 실근하나 허근하나 인 경우는 없다.
왜냐면 실근이라는건 실수인 근이라는거고
허근이라는건 허수인 근이라는건데
근의 공식을 보자.

여기서 핵심은 루트 부분이다.

저 루트 안에있는 b²-4ac 의 값이
음수면 허근인거고
그 외에는 실근인것이다.
'음수의 제곱근은 허수'라고 얘기했었다.

근데 근의 공식에 근거하여
저 루트값에 +붙인거랑 -붙인거
이 두개가 근으로 나오는건데
a, b, c 모두 상수이므로
b²-4ac도 상수이다. 즉 변하지 않는 값이다.
따라서 b²-4ac는 양수거나, 0이거나, 음수거나 셋중 하나일것이며
따라서 근 하나가 실근이면 나머지 하나도 무조건 실근이고
근 하나가 허근이면 나머지 하나도 무조건 허근이다.
따라서 이차방정식은
실근 두개를 갖거나, 허근 두개를 갖는다.
라는 결론에 다다른다.
- 이차방정식의 근의 판별법 -
대충 가닥을 잡았으니 제대로 판별해볼 차례이다.

일단 근을 직접 구해볼까?
인수분해는 하는방법 안보이니까
근의공식으로 구해보자.

따라서 답은
'두 실근을 갖는다.'
근데 근의공식을 안써도 그냥 구할수 있다.
아까 근의공식에서 핵심이라 했던 부분을 다시보자.
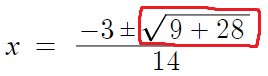
왜 이부분이 핵심인가?
9+28 이라는 값이 음수라면
음수의 제곱근이기 때문에 허수가 나올것이기 때문이다.
즉 근이 실근인지, 허근인지 판별할때는
근의공식을 다 쓰지 않아도
저 루트 안에 있는것의 부호만 가지고 판별할수 있다.
9+28은 양수니까 두 실근을 갖는다. 라고 할수 있는거다.
- 근의 판별법 일반화 -
근을 판별할때는
근의 공식에서 뭐만 본다?
루트 안의 것만 본다.
왜냐면 루트 안의 값이 음수면 허근이고
그게 아니면 실근이기 때문이다.
나머지는 관심없다. 실근, 허근만 구별하면 되기때문이다.

즉, 여기서 루트 안의 것인
b²-4ac 의 부호만 알면 된다.
여기서 b²-4ac를
판별식이라 부르며, D라고 쓴다.
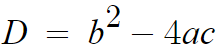
D의 부호에 따라서,
실근인지 허근인지 판별할 수 있다.
D가 양수면
양수의 제곱근은 실수이기 때문에
두 실근을 갖고
D가 음수면
음수의 제곱근은 허수이기 때문에
두 허근을 갖는다.
근데 D가 0이면?
이것도 일단 0의 제곱근은 실수이기 때문에
두 실근을 갖긴 하는데
이건 좀 특이한케이스라 약간의 설명이 필요하다.
근의공식 자리에 판별식 D만 넣어서 다시써보자.
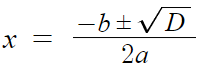
여기서 D=0 이라면?
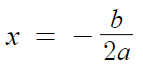
x= -b/2a 라고 하나밖에 안 나온다.
그 외에 근은 없다.
근이 한개인것 같지만
이차방정식은 무조건 두개의 근을 가진다는
자명한 논리를 깰수는 없으므로
근은 두개가 맞다.
두 실근을 갖긴 하는데
두 실근의 값이 같은것이라 봐야한다.
따라서 이때는
서로 같은 두 실근을 갖는다 라고 하며
이런걸 '중근'을 갖는다 라고 표현한다.
따라서 정리하자면

a : 이차항의 계수
b : 일차항의 계수
c : 상수항
이라는건 설명안해도 알것이라 믿는다.
- 예제 -
1 )
이차방정식에서,
판별식이 0보다 작으면
서로 다른 두 허근을 갖게 된다.
그 이유를 설명하시오.
판별식은 b²-4ac 이며
'근의공식'에서 따온것이다.
왜 근의공식에서 따왔냐면
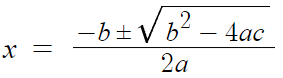
이게 근의공식인데
여기서 루트 안에 있는것이 양수냐, 음수냐에 따라
근이 실수냐, 허수냐가 정해지는건데
루트 안에 있는것이 바로 판별식인 b²-4ac 이고
판별식인 b²-4ac 이 0보다 작으면
음수의 제곱근이라 허수가 나올것이기 때문이다.
이거랑 완벽히 똑같이는 아니어도
이정도로는 설명할수 있어야한다.
'설명할수 없다 = 모른다'
2 )

판별식 D = b²-4ac 에서
a=4, b=-12, c=9 이므로
D = 144-144 = 0 이다.
D=0 이므로
답은 '중근을 갖는다' 또는 '같은 두 실근을 갖는다'
3 )


따라서 답은
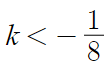
'수학(상) > II. 방정식' 카테고리의 다른 글
| 이차방정식 #4 - 이차식의 인수분해 (0) | 2022.01.21 |
|---|---|
| 이차방정식 #3 - 근과 계수의 관계 (0) | 2022.01.16 |
| 이차방정식 #1 - 이차방정식의 풀이 (0) | 2022.01.14 |
| 복소수 #3 - 복소수의 사칙연산, 음수의 제곱근 (0) | 2022.01.14 |
| 복소수 #2 - 복소수의 뜻과 켤레복소수 (0) | 2022.01.11 |



