
- 개요 -
고1 수학을 통틀어 가장 중요한곳이며
여기서 나온거 고2, 고3때 또나오고 또나오고 맨날나온다.
대신 고2, 고3때는
고1때 배웠으니까 이정도는 알지? 하고 넘어가버린다.
따라서 여기서 제대로 개념을 잡아놔야한다.
그래서 여기는 천천히 진행할것이다.
- 근데 방정식단원에서 뜬금없이 복소수는 왜 배웠는가? -
이 부분이 조금 의아했을 수 있다.
복소수는 그냥 숫자 체계의 추가개념 느낌인데
왜 방정식 단원에 있는건가?
이유는 간단하다.
'허수'라는것의 존재를 이해해야 방정식을 제대로 풀수 있다.
- 방정식이란 무엇인가? -
우선 '등식'이 뭔지 복습해보자.

이런식으로 두 식을 등호 '=' 로 연결한 식을 말한다.
저 등식이 성립하는지, 성립하지 않는지는
어떤 방정식이냐에 따라 다르다.
만약 아래와 같은 등식이 있다고 해보자.

이 식은 문자 x에 대한 식인데
x값에 상관없이 무조건 성립하는, 너무 당연한 식이다.
따라서 항상 같은 등식 이라는 뜻에서
'항등식' 이라고 한다.
하지만 이런 등식은 좀 다르다.

이 식도 문자 x에 대한 식인데
x=3 일때만 성립한다.
이런식으로 문자에 특정한 값을 주었을 때만 성립하는 식을
'방정식' 이라고 한다.
따라서 등식은 항등식이거나, 방정식이거나
둘중 하나이다.
항등식이 아니면 방정식인것이다.
즉 '방정식 = 등식인데 항등식이 아닌것'
만약 문자에 어떤 값을 넣어도 성립하지 않는 등식이라면?
그것도 방정식이긴 하다. 근이 존재하지 않는 방정식인것이다.
이런걸 특별히 '불능' 이라 하며,
이런건 애초에 '잘못 세워진 방정식' 이므로
신경쓰지 않아도 된다.
예를 들자면 이런거

- 방정식의 실근과 허근 -
그래서 허수랑 방정식이랑 무슨상관인가?

우선 이건 이차식이고, 방정식이니까 이차방정식이다.
그리고 이차방정식이므로 무조건 두 개의 근을 가져야 한다.
근데 허수라는걸 배우기 전에는 이걸 설명하지 못했을거다.
왜냐면 제곱해서 음수가 되는 수 따위는 실수의 범위 내에서 존재하지 않기때문이다.
그래서 뭘 말하려는거냐면
이차방정식은 무조건 두개의 근을 갖는데,
그 근은 실수일수도 있고, 허수일수도 있다.
여기서 실수와 허수를 모두 포괄하고있는 수가 바로 '복소수'이다.
따라서, 다음과 같은 결론을 얻는다.
이차방정식은 복소수의 범위에서 무조건 두개의 근을 갖는다.
그리고 여기서
실근 : 실수인 근
허근 : 허수인 근
예를 들어,

이 이차방정식의 근은 -1, 1 이므로
'두 실근'을 갖는다.

이 이차방정식의 근은 -i, i 이므로
'두 허근'을 갖는다.
추가로, 이차방정식 뿐만이 아니라
삼차방정식도 무조건 3개의 근을 갖고
100차방정식도 무조건 100개의 근을 갖는다.
- 이차방정식의 풀이법 1 : 근의공식 -
풀이법이라는건 '근을 구하는 방법' 말하는거다.
이차방정식에서 근을 구하는 방법을 알려줄거다.

이차방정식의 근은
근의 공식을 이용해서 구할수 있다.

'까먹었어요' 라고 하려 했다면
그건 말도안되는소리다.
까먹었다는건 그냥 외웠다는거고
근의공식부터 공부하고와야한다.
근의공식은 중3수학이긴 한데 증명을 한번더 보여주겠다.
이 증명 과정은 스스로 할수 있어야하며
왜 이렇게 증명해야하는지도 설명할수 있어야한다.

핵심 논리 : 일차방정식은 풀기 쉽다.
따라서 이차방정식을 일차방정식으로 바꿀거다.
일차방정식으로 만들기 위해
완전제곱식으로 만든 뒤 근호를 씌운다.
이제 직접 근을 구해볼차례이다.
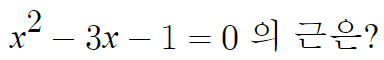
근의 공식을 적용하면

여기서 a=1, b=-3, c=-1 이니까
전부 대입해주면
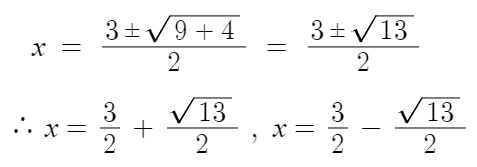
- 예제문제로 연습 -

우선 근의공식을 쓰려면
이차방정식이
ax²+bx+c=0 이런 형태여야한다.
즉 전개된 식이어야 하며, 우변이 0이어야 한다.
우변은 이미 0이니까
좌변을 전개만 해주면 근의공식을 쓸수 있을것이다.

이제 근의공식을 써주자.

a=1, b=1, c=-6 이니까
대입해서 정리하면

따라서 답은
x=2, x=-3
- 이차방정식의 풀이법 2 : 인수분해 -
근의 공식을 이용한 풀이와는 조금 방향이 다르다.
근의공식은 전개된 식에서 썼다면
이 풀이는 인수분해된 식에서 쓴다.
인수분해된 식을 전개해서 근의공식을 써도 되고,
전개된 식을 인수분해해서 풀어도 되는것이다.
이 풀이법의 기본 논리를 설명해주겠다.
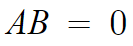
AB=0 이라면
A와 B의 곱이 0이 되기 위해
A=0 이거나
B=0 이거나
둘다 0이거나
이 셋중 하나일것이다.
어쨌든 확실한건
'A와 B중 하나는 무조건 0이다'
여기서 A와 B 자리에
일차식을 넣어볼까?
A = x-2 라 하고
B = x+3 이라 하면
A×B는 일차식×일차식 이니까 이차식이 될것이다.

(x-2)(x+3)=0 이라면
(x-2)와 (x+3)의 곱이 0이 되기 위해
(x-2)=0 이거나
(x+3)=0 이거나
둘다 0이거나
이 셋중 하나일것이다.
어쨌든 확실한건
'(x-2)와 (x+3)중 하나는 무조건 0이다'
x-2=0 을 만족시키는 x값은 2
x+3=0 을 만족시키는 x값은 -3
따라서
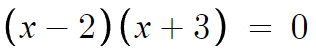
이 식은 x=2 또는 x=-3
을 만족해야만 한다.
그래야 곱해서 0이 될수 있다.
따라서 이 방정식의 근은
x=2 , x=-3 이다.
근데 이거 아까 근의공식풀이 예제로 나왔던 문제이다.
전개하고 근의 공식을 쓰는 고생을 하지 않아도
눈으로 5초면 풀수 있는문제였던것이다.
즉 인수분해를 이용하는게 압도적으로 빠르고 쉽다.
이건 이 문제만 그런게 아니라,
대부분의 문제가 그렇다.
따라서 다음과 같은 결론을 얻는다.
이차방정식을 풀때는,
인수분해를 이용하는 방법을 우선순위로 두고,
인수분해가 안되면 근의공식으로 푼다.
물론 근의공식으로 풀어도 되지만
인수분해는 고등수학 3년 내내 함께하면서
익숙해질수밖에 없고
나중엔 안시켜도 알아서 인수분해하는 방법으로 풀게되니까
당장은 크게 신경쓰지 않아도 된다.
직접 풀어보자.

x²-x-20 을 인수분해하면
(x-5)(x+4) 이다.

(x-5)(x+4) = 0 이려면
(x-5)=0 이거나
(x+4)=0 이거나
둘다 0이거나
셋중 하나여야한다.
따라서
'(x-5)와 (x+4)중 하나는 무조건 0이다'
따라서 답은
x=5, x=-4 이다.
인수분해만 하면 끝나버린다.
근의공식보다 간편하지 않은가?
많이 연습해서 익숙해져야한다.
- 예제 -
1 )


여기서 a=9, b=-6, c=1 이다.
각각 대입해서 정리하면

따라서 답은 x=1/3
문제까진 문제없이 풀수 있을텐데
여기서 질문이 있을수 있다.
Q) 이차방정식은 무조건 근이 두개라면서요?
저것도 근이 두개이다. x=1/3과 x=1/3 이다.
두 근이 서로 같은것 뿐이다.
즉 '서로 같은 두 실근'을 갖는것이다.
이런걸 '중근을 갖는다' 라고 하는데
자세한건 다음에 다룰내용이니 거기서 설명해주겠다.
2 )

9x²-6x+1 을 인수분해하면

따라서 3x-1=0 이어야한다.
이게 성립하는 x값은 1/3 뿐이고
따라서 답은 x=1/3
3 )

우선 인수분해가 편하다는건 직접 해보면서 느꼈을테니까
일단 인수분해하는 방법으로 해보자.
근데 아무리 노력해도
3x²-4x+2 는 인수분해가 잘 안된다.
인수분해가 잘 안된다 싶으면 근의공식을 쓰면 되는거다.

여기서 a=3, b=-4, c=2 이니까
각각 대입해서 정리하면

따라서 답은

추가로, 실근을 갖냐 허근을 갖냐로 물으면
허근을 갖는다고까지 대답할수 있어야한다.
그리고 인수분해가 잘 안됐던 이유를 알았다.
허수인데다가 루트까지 들어갔기 때문에 인수분해가 어려웠던것이다.
'수학(상) > II. 방정식' 카테고리의 다른 글
| 이차방정식 #3 - 근과 계수의 관계 (0) | 2022.01.16 |
|---|---|
| 이차방정식 #2 - 근의 판별 (0) | 2022.01.16 |
| 복소수 #3 - 복소수의 사칙연산, 음수의 제곱근 (0) | 2022.01.14 |
| 복소수 #2 - 복소수의 뜻과 켤레복소수 (0) | 2022.01.11 |
| 복소수 #1 - 허수란 무엇인가? (0) | 2022.01.10 |



