
고등수학에서 첫번째 고비는 허수였다.
두번째 고비가 찾아왔다.
본격적으로 수포자들이 많아지는 곳이기도 하다.
- 중등수학 복습 : 함수란 무엇인가? -
우선 '함수'라는게 뭐였는지부터 복습을 해보자.
사실 여기 별로 어려운곳 아닌데 학생들이 어려워하는 이유가
함수가 뭔지 몰라서그런거라고 생각한다.
함수가 뭔지 모르니 당연히 이차함수도 못하는것이다.
두 변수 x, y가 있다고 해보자.
만약 x의 값에 따라 y의 값이 정해진다면
이럴때 'y'를 'x에 대한 함수' 라고 한다.
x에 대한 함수 는
함수가 영어로 function이고 앞글자인 f를 따와서
x에 대한 함수(f)라는 뜻으로 f(x) 라고 표현하고
따라서 y=f(x) 라고 쓸수 있다.
f(x)는 y의 값이고
또 f(x)가 x의 함수이므로
f(x)는 함숫값이다.
문자만 바꿔서 똑같이 한번더 말해주겠다.
두 변수 a, b가 있다.
만약 a의 값에 따라 b의 값이 정해진다면
이럴때 'b'를 'a에 대한 함수' 라고 한다.
a에 대한 함수는 f(a) 라고 표현하고
따라서 b=f(a) 라고 쓸수 있다.
f(a)는 b의 값이고
또 f(a)가 a의 함수이므로
f(a)는 함숫값이다.
- 점검문제 -
두 변수 x,y가 있다고 해보자.
이 두 변수의 값은
y = 3x+1 라는 관계를 가진다.
1. y는 x에 대한 함수인가?
함수라면 y는 x에 대한 함수라는것을 수학적 기호로 표현하고,
함수가 아니면 그 이유를 설명하시오.
2. x는 y에 대한 함수인가?
함수라면 x는 y에 대한 함수라는것을 수학적 기호로 표현하고,
함수가 아니면 그 이유를 설명하시오.
3. y=f(x)라고 하면,
f(0)이 의미하는것은 무엇이며 그 값은 무엇인가?
두 변수 x와 y 사이에
y=3x+1 이라는 관계가 있다는건
x의 값에 따라서 y값이 정해진다는것
따라서 y는 x에 대한 함수이다.
y=f(x)라고 표현할수 있다.
두 변수 x와 y 사이에
y=3x+1 이라는 관계가 있다는건
+1을 이항하면 y-1 = 3x
양변에 3을 나눠주면 (y-1)/3 = x
따라서 y의 값에 따라서 x의 값이 정해진다.
따라서 x는 y에 대한 함수이다.
x=f(y)라고 표현할수 있다.
y=f(x) 라고 하면,
y는 x에 대한 함수라는 말이다.
f(0) 이라는건
f(x)라는 함수에 x=0을 대입해서 계산했을 때 나오는 값이다.
즉 f(0)은 함수 f(x)의 x=0에서의 함숫값이다.
y=3x+1 이므로 f(x)=3x+1 이다.
따라서 f(0) = 1이다.
- 이차함수란? -
간단하다.
y=f(x) 라고 해보자.
y는 x에 대한 함수이다.
여기서 f(x)가 x에 대한 이차식일 때를
이차함수라고 한다.
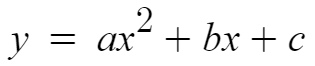
이게 이차함수이다.
정확히 말하자면, y는 x에 대한 이차함수
요약하자면,
함수인데 이차식이면 이차함수이다.
- 함수와 방정식의 차이점 -
함수와 방정식의 차이점이 무엇일까?

이게 이차함수고
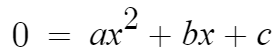
이게 이차방정식이다.
f(x)는 함수이고,
x의 값에 따라 변하는 변수이며,
x값에 따라 함숫값도 정해진다.
따라서 f(x)의 값은 0일수도 있고, 0이 아닐수도 있다.
만약 f(x)값이 0이면 방정식이랑 완전히 생김새가 똑같아질텐데
그럼 뭐가다른건가?
방정식의 목적이 무엇인지를 짚어볼 필요가 있다.
'방정식의 목적'이 뭔가?
현재 키 130cm인 아이가 매일 키가 0.1cm씩 자란다고 해보자.
그럼 키가 140cm가 될때는 현재부터 며칠 후인가?
이 문제는 '방정식을 세워서' 푼다.
무슨 말이냐면,
'며칠 후' 인지를 미지수로 두고
그 미지수에 대한 관계식을 써낸다음 정리하면
그 미지수의 값을 알아낼 수 있다는거다.
며칠 후인지를 미지수 x라 두고 방정식을 세우면
130 + 0.1x = 140
따라서 x=100 이고
아이는 100일 후 140cm가 된다.
'왜' 방정식을 세웠는가?
'며칠 후'에 키가 140cm가 되는지 알아내려고
따라서 방정식의 목적은
'등식이 성립하도록 하는 미지수의 값' 을 구하는데에 있다.
함수와 방정식의 차이가 여기서 나온다.
방정식은 '키가 140cm가 되는 시점' 에 초점을 두고있다면
함수는 '아이의 키' 그 자체에 초점을 두고있다.
아이의 x일 후 키를 함수 f(x)라 하면
f(x) = 130 + 0.1x 이다.
여기서 x값만 대입하면 아이의 키가 나오는것이다.
100일 후 키는? x=100 대입하면 f(100) = 140
250일 후 키는? x=250 대입하면 f(250) = 155
- 이차함수와 이차방정식의 관계 -
x에 대한 이차함수 y가 있다고 해보자.

이 함수의 그래프부터 그려볼것이다.
함수의 그래프라는것은
이 함수가 나타내는 선을 말하는건데
뭘 나타내는거냐?
x값이 있으면 그것에 대응되는 y값이 있을것 아닌가?
그럼 xy 평면좌표계에서 (x,y)의 위치를 점으로 찍을수 있다.
근데 x는 변수이다. x값은 하나가 아니다.
수많은 x값이 있고
그것에 대응되는 수많은 y값이 있을것이다.
그러면 수많은 (x,y) 를 나타내는 점이 생길거고
그 점을 모두 이은게 바로 함수의 그래프이다.
쉽게 요약하자면,
그래프를 그리고싶으면, 점을 여러개 찍은다음 이으면 된다.
이차함수중에서 가장 간단한걸로 가져와서 같이 그래프를 그려보자.
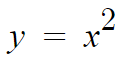
x=0 일때 y=0 이다.
x=1 일때 y=1 이다.
x=2 일때 y=4 이다.
x=3 일때 y=9 이다.
x=-1 일때 y=1 이다.
x=-2 일때 y=4 이다.
x=-3 일때 y=9 이다.
이것들을 모두 점으로 찍으면
아래와 같이 된다.

이것들을 부드럽게 이어주면 그래프를 그릴수 있다.
물론 정확히 그리려면 x=0.5, x=0.1, x=0.01 이런식으로
아주 세분화해서 전부 구해봐야겠지만
그럴수는 없으니 일단 적당히 포물선모양 나오게 그려주자.
이번 주제는
그래프를 정확히 그려내는게 목적이 아니라
'함수의 그래프와 방정식 사이에 어떤 관계가 있는지'를 설명하는게 목적이라
대충 그려도 된다.

그래서 그래프는 왜 그렸냐면
저 그래프를 잘 보자.
x축과 만나는 지점이 있는데
x=0 인 지점이다.
왜 x축과 만나냐면
x=0 일때 y=0이기 때문이다.
y=0 이라는건 y가 함수기때문에 함숫값이 0이라는것
함숫값이 0이면 x²=0 이고
이차방정식과 형태가 똑같아진다.
즉, 함수의 그래프가 x축과 만나는 지점이 어딘지 알고싶다면
x축과 만난다는건 함숫값이 0이 된다는거니까
f(x)=0 이라는 방정식을 세워서 근을 구하면 된다.
예를 들어, 함수 y=x²가 x축과 만나는 지점을 알고싶다?
x축과 만난다는건 y=0 이라는거니까
이차방정식 0=x² 를 세운다음 풀면 된다. 근은 x=0 이다.
따라서 함수 y=x² 은 x=0 에서 x축과 만난다.
따라서 아래와 같은 결론을 얻는다.
함숫값이 0이 되도록 하는 x값
=
방정식의 근이 되는 x값
그니까 쉽게말해서
함수 f(x)가 있다고 하면
f(x)의 값이 0이 되도록 하는 x값은
방정식 f(x)=0 의 근과 같다.
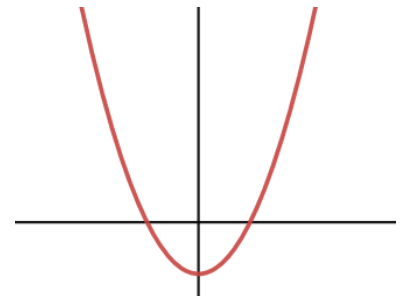
함수 f(x)가 이렇게 있다고 하면

표시한 부분이 바로 f(x)=0 이 되도록 하는 x값이라는거다.
이럴거면 그냥 방정식쓰면 되지 왜 굳이 함수를 쓰느냐 할수 있는데
무슨 의미가 있냐면
이 함수의 그래프가 'x축과 만난다' 는 것이다.
즉 함수 f(x)가 x축과 만나는 x값을 알고싶다면
f(x)=0 이라는 방정식을 세운다음 그것의 근을 구하면 되는것이다.
따라서 요약하자면,
함수와 방정식이 무슨 관계냐고 하면
'함수의 그래프'와
'방정식의 근'
이 둘 사이에 밀접한 관계가 있다고 하면된다.
함수의 그래프가 x축과 만나는 지점이 곧 방정식의 근이기 때문이다.
- 일반화 -

이런 이차함수가 있다고 해보자.
이 이차함수의 그래프가 x축과 만나는 지점의 x값은
y=0이 되도록 하는 x값을 의미하고

위 이차방정식의 근을 구하면
거기가 바로 x축과 만나는 지점의 x값이다.
이차함수 y=ax²+bx+c 의 그래프와 x축의 교점의 x좌표는
이차방정식 ax²+bx+c=0 의 실근과 같다.
- 이차함수의 그래프와 이차방정식의 근 -
조금 이해 안가는 부분이 있을텐데
함수가 꼭 x축과 만날필요는 없지않나?
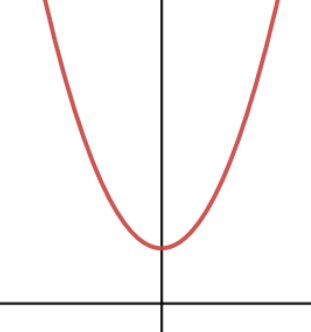
이렇게 생긴 함수면 안만나는거 아닌가?
맞는 말이다.
안만난다는건 함숫값이 0이되는 x값이
실수의 범위 내에서 존재하지 않는다는것이다.
즉 함수의 그래프가 x축과 만나지 않으면
실근을 갖지 않는다.
만약 이차함수 y=ax²+bx+c 가 x축과 만나지 않는다면,
이차방정식 0=ax²+bx+c 에서 실근이 존재하지 않는다는거고
이는 곧 두 허근을 갖는다는 말이다.
보다시피, '방정식에서 실근, 허근 여부'만 판단하면
함수의 그래프가 x축과 만나는지, 안만나는지 알 수 있다.
여기서 다룰건 이차함수니까
이차방정식의 실근, 허근 여부를 판별하면 된다.
방정식의 실근, 허근 여부 판별법은?
'판별식'을 쓰면 된다.

D>0 이면 서로다른 두 실근을 갖는거니까
이차함수의 그래프가 x축과 '두번' 만날것이다.
D=0 이면 중근을 갖는거니까
이차함수의 그래프가 x축과 '한번' 만날것이다.
D<0 이면 서로다른 두 허근을 갖는거니까
이차함수의 그래프가 x축과 만나지 않을것이다.
- 예제 -
1 )

함수의 그래프와 x축의 교점이라는건
함수의 그래프와 x축이 만난다 = 함숫값이 0이다
따라서 y=0이다.
따라서 0 = x²+x-2 를 만족하는 x값을 구하면
거기가 바로 y=0이 되도록 하는 x값인거고
그게 곧 교점의 x좌표인거다.
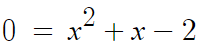
이 이차방정식의 근은
인수분해를 이용하면
x²+x-2 = (x-1)(x+2) = 0 이고
이것의 근은 x=1, x=-2 이다.
따라서 답은 x=1, x=-2
2 )

함수가 좀더 복잡하게 생겼지만
문제에서 묻는건 똑같기때문에 그냥 똑같이풀면된다.
함수의 그래프와 x축이 만난다 = 함숫값이 0이다
따라서 y=0이다.
따라서 0 = -4x²+12x-9 를 만족하는 x값을 구하면
거기가 바로 y=0이 되도록 하는 x값인거고
그게 곧 교점의 x좌표인거다.
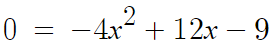
이 이차방정식의 근은
-4x²+12x-9 = 0 여기서 이차항 계수가 음수인게 꼴보기 싫으니
양수로 바꾸기 위해 양변에 -1을 곱해주면
4x²-12x+9 = 0
인수분해해주면
4x²-12x+9 = (2x-3)² = 0
이것의 근은 x=1.5 이다.
따라서 답은 x=1.5
3 )

이차함수의 그래프와 x축의 교점의 개수를 찾으라는건
y=0 이 되도록 하는 x값의 개수 를 찾으라는것
y=0 이라는건
이차방정식 0 = -4x²+4x-1 이 실근을 갖는다는것
두번 만나면 서로다른 두 실근
한번 만나면 중근
안 만나면 서로다른 두 허근
0 = -4x²+4x-1 의 근을 판별하기 위해 판별식을 이용하자.
D = b² - 4ac 인데
여기서 b=4, a=-4, c=-1 이다.
각각 대입해서 정리하면 D = 0 이다.
D=0 이므로 0 = -4x²+4x-1 은 중근을 갖는다.
따라서 y = -4x²+4x-1 의 그래프는 x축과 한번 만난다.
따라서 답은 1
'수학(상) > II. 방정식' 카테고리의 다른 글
| 이차함수 #3 - 이차함수의 그래프 그리기와 평행이동 (0) | 2022.01.28 |
|---|---|
| 이차함수 #2 - 이차함수의 그래프와 직선의 위치 관계 (0) | 2022.01.26 |
| 이차방정식 #5 - 이차방정식의 켤레근 (0) | 2022.01.22 |
| 이차방정식 #4 - 이차식의 인수분해 (0) | 2022.01.21 |
| 이차방정식 #3 - 근과 계수의 관계 (0) | 2022.01.16 |



