
- 개요 -
이번에 다룰 것은
이차부등식을 풀기 위한 사전 지식이다.
이차부등식을 풀기 위해서는
이차부등식과 이차함수가 무슨 관계가 있는지 알아야한다.
똑같이 생긴 식의
이차부등식과 이차함수가 있다고 해보자.
이차부등식이 뭔지는 굳이 설명하지 않아도 알것이라 생각한다.

부등식과 방정식은 푸는 방법이 거의 동일하다.
즉 부등식과 방정식은 밀접한 관계가 있고
방정식과 함수는 함숫값이 0이 되는 지점을 중점으로 두고 분석한다.
즉 방정식과 함수가 밀접한 관계가 있다.
이처럼 부등식과 함수도 밀접한 관계가 있다.
이번에 그걸 다룰것이다.
- 쉬운것부터 : 일차부등식과 일차함수의 관계 -

부등식과 방정식의 풀이법이 같기때문에
부등식과 함수의 관계를 분석할때도 같은 방법을 쓴다.
함숫값이 0 이 되는 지점을 중점으로 두고 분석한다.
함숫값이 0이 된다는건
곧 방정식 f(x)=0 를 만족한다는거고
따라서 '함수의 그래프'와 '방정식의 근'
이 둘 사이에 밀접한 관계가 있다.
함수의 그래프가 x축과 만나는 지점이 곧 방정식의 근이기 때문이다.
그래서 부등식은 어떻게푸는건가?
똑같다.
함숫값이 0보다 크다는건
곧 부등식 f(x)>0 을 만족한다는거고
따라서 '함수의 그래프'와 '부등식의 해'
이 둘 사이에 밀접한 관계가 있다.
함수의 그래프가 x축과 만나는 지점이 곧 부등식의 해를 구하는 기준이기 때문이다.
직접 해볼까?

f(x)>0 의 해는
함수 f(x)의 값이 0보다 크게 되도록 하는 x값을 구하면 된다.
근데 f(x) = x-1 이니까
x-1 의 값이 0보다 크게 되도록 하는 x값을 구하면 된다.
따라서 x-1>0 이 되도록 하는 x값을 구하면 된다.
따라서 답은 x>1
그래프를 그려서 풀어도 된다.
개인적으로 이차부등식부터는 복잡해지기 때문에
그래프를 그려서 푸는것을 권장한다.
f(x)의 그래프를 그리면

여기서 f(x)가 0보다 크도록 하는 x의 범위는?
f(x)는 x=1에서 0이 되고
x=1을 기준으로 f(x)가 양수로 변한다.
따라서 이를 만족하는 x값의 범위는 x>1 이다.
따라서 답은 x>1
- 이차부등식과 이차함수의 관계 -

이것의 해는
아까도 설명했듯이 f(x)>0 이 되도록 하는 x값이고
f(x)>0 이라는것은
f(x)의 그래프를 그렸을때,
그래프가 y=0(x축) 보다 위에 있다는것
즉 f(x)의 그래프가 x축보다 위에 있도록 하는 x값의 범위를 구하면 된다.
그냥 이차방정식과 이차함수의 관계랑 같은 논리로 푸는거라서
딱히 추가설명할게 없다.
그래도
" f(x)>0 이라는건 f(x)의 그래프가 x축보다 위에 있다는 뜻이다. "
라는 정도로는 설명할수 있어야 문제를 풀수 있다.
그럼 반대로 ax²+bx+c<0 이라면?
f(x) = ax²+bx+c 라 하고
f(x)의 그래프를 그리면
f(x)의 그래프가 x축보다 아래에 있도록 하는
x값의 범위를 구하면 되는거다.
핵심 논리는,
이차부등식을 분석할때는
이차식을 이차함수로 놓고 그래프를 그린다.
그러면 어느 지점에서 0보다 작아지는지, 또는 커지는지 바로 알수 있기때문에
직관적이고 효율적인 분석이 가능하다.
- 예제 -
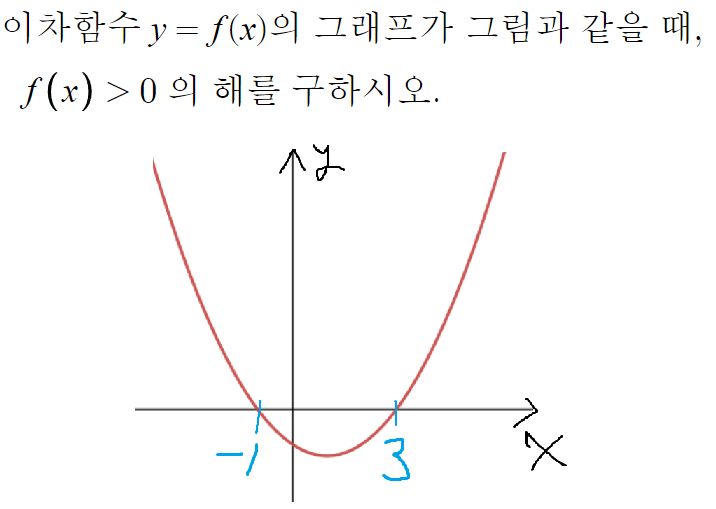
f(x)>0 이라는건
f(x)의 그래프를 그렸을 때
그 그래프가 x축 위에 있게 된다는것
그런 x값의 범위는 x<-1 또는 x>3 이다.
따라서 답은 x<-1 또는 x>3
'수학(상) > III. 부등식' 카테고리의 다른 글
| 이차부등식 #4 - 연립이차부등식 (0) | 2022.02.18 |
|---|---|
| 이차부등식 #3 - 이차부등식의 작성 (0) | 2022.02.18 |
| 이차부등식 #2 - 이차부등식의 풀이, 항상 성립할 조건 (0) | 2022.02.14 |
| 절댓값 기호를 포함한 부등식 (0) | 2022.02.08 |
| 연립일차부등식 (0) | 2022.02.07 |



