
- 이차부등식의 작성 -

이런 문제를 풀어볼거다.
어떻게 푸느냐?
우리가 이차부등식을 풀때 썼던 방법을 또 쓴다.
그래프를 그리는거다.
x²의 계수가 1이니까 아래로 볼록하게 그려질것이고
해가 -1<x<7 이라는건
x=-1, x=7 에서 x축과 만난다는뜻이니까
아래처럼 그려질것이다.

여기서 해가 -1<x<7 이라는건
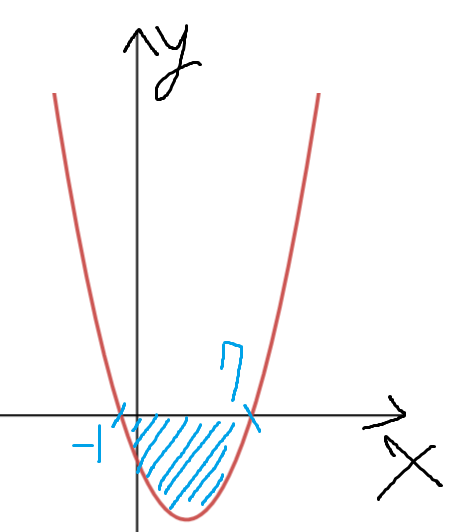
파랗게 칠한부분을 뜻하는거고
이는 곧 x축보다 아래에 있는 범위를 말하는거다.
따라서 이 이차부등식의 형태는
x²+ax+b<0 이다.
a와 b의 값을 구하면 되는데
우리가 이차부등식을 풀때 썼던 방법을 되새겨보면 간단하다.
x축과 만나는 지점을 찾는것이다.
x축과 만나는 지점은 곧
우리가 작성하고자 하는 이차식인 x²+ax+b = 0 을 만족하는 곳이고
거기가 x=-1, x=7 이라고 하니
이차식에서 근과 계수의 관계에 의해
a = -(-1+7) = -6
b = (-1)×7 = -7
따라서 답은 x²-6x-7

따라서 요약하자면
1. 주어진 해의 의미를 파악한다.(그래프를 그리면 쉽다)
2. 근과 계수의 관계를 이용해 계수를 구하여 마무리한다.
- 예제 -

더보기
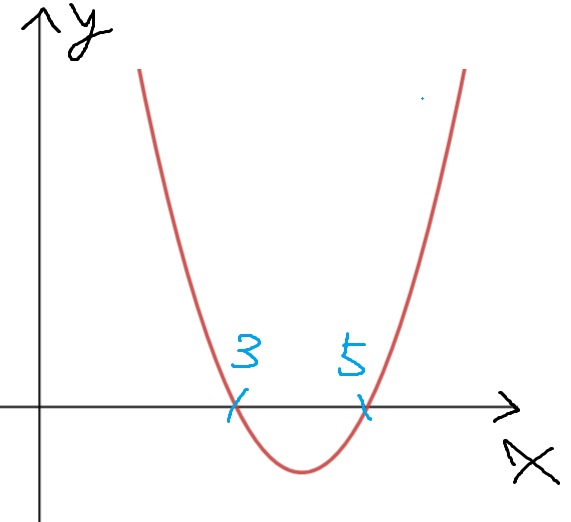
우선 이차항의 계수가 양수인것과
그래프가 x=3, x=5에서 x축과 만남을 이용하여
그래프를 그려보면

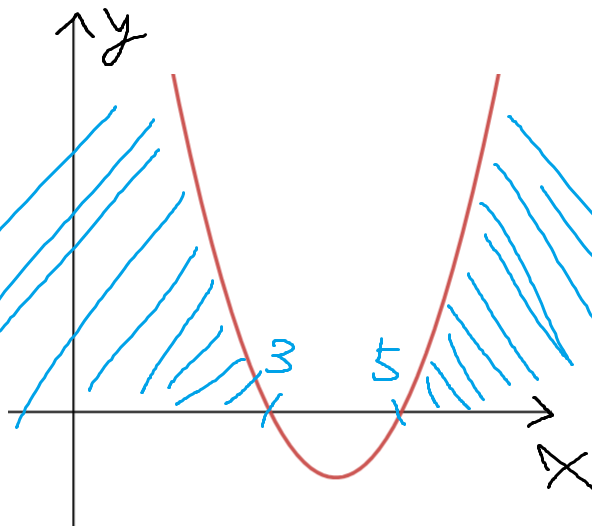
x≤3 또는 x≥5 인 부분을 표시하면 아래와 같다.

이것의 의미는 x축 또는 x축보다 위에 있는 범위 이며
따라서 여기까지 이차부등식의 형태를 잡아보면
x²+ax+b≥0 이다.
근과 계수의 관계에 의해
a = -(3+5) = -8
b = 3×5 =15
따라서 답은 x²-8x+15 ≥ 0
'수학(상) > III. 부등식' 카테고리의 다른 글
| 이차부등식 #4 - 연립이차부등식 (0) | 2022.02.18 |
|---|---|
| 이차부등식 #2 - 이차부등식의 풀이, 항상 성립할 조건 (0) | 2022.02.14 |
| 이차부등식 #1 - 이차부등식과 이차함수의 관계 (0) | 2022.02.13 |
| 절댓값 기호를 포함한 부등식 (0) | 2022.02.08 |
| 연립일차부등식 (0) | 2022.02.07 |



