
- 개요 -
개인적으로 아주 쉬운곳이다.
공식이 있긴한데 하나도 외울필요가 없는게
식을 써서 증명하는 그런 복잡한 방법으로 나온 공식이 아니라
지극히 상식적인 것들만 있다.
- 핵심 -
집합의 연산에 관해
여러가지 성질이 있는데
이를 이해하는 가장 쉽고 효율적인 도구는
'벤 다이어그램' 이다.
이것만 그리면 모든문제가 다풀린다.
- 집합의 연산법칙 -

다항식의 연산법칙과 똑같다.
집합을 연산할때 다항식 연산할때처럼 취급해도 된다는뜻이다.
다항식처럼 교환법칙, 결합법칙, 분배법칙이 성립한다.
주의할건, 합집합과 교집합에서만 성립한다.
헷갈리기 쉬우니 그냥 벤다이어그램 그리자.
- 집합의 연산의 성질 -
지극히 상식적인 것들이라 자세히 설명하지는 않겠다.
혹시 이해가 안된다면, 벤다이어그램을 그려보면 바로 이해가 될것이다.
전체집합 U의 두 부분집합 A, B에 대해서
1. A와 A의 합집합은 A이다.

당연히 자기자신과 합집합하면 자기자신이 나온다.
2. A와 A의 교집합은 A이다.

당연히 자기자신과 교집합하면 자기자신이 나온다.
3. A와 공집합의 합집합은 A이다.

당연히 아무것도없는것과 합집합하면 자기자신이 나온다.
4. A와 공집합의 교집합은 공집합이다.

당연히 아무것도 없는 집합(공집합)과 교집합하면 공집합이 나온다.
5. A와 U의 합집합은 U이다.

A가 U의 부분집합이니, 당연히 둘을 합집합 연산하면 U가 나온다.
6. A와 U의 교집합은 A이다.

A가 U의 부분집합이니, 당연히 둘을 교집합 연산하면 A가 나온다.
7. 전체집합의 여집합은 공집합이다.

전체집합 = 모든게 있는집합
따라서 전체집합의 여집합은 아무것도 없는집합, 즉 공집합이다.
8. 공집합의 여집합은 전체집합이다.
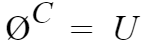
공집합 = 아무것도 없는집합
따라서 공집합의 여집합은 모든게 있는 집합, 즉 전체집합이다.
9. A의 여집합의 여집합은 A이다.
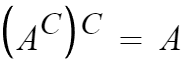
글로 풀어써서 좀 어려워보이지만 사실 당연한것이다.
A의 여집합 = A가 아닌것
A의 여집합의 여집합 = A가 아닌것이 아닌것. 즉 A가 맞는것
10. A와 A의 여집합의 합집합은 전체집합이다.
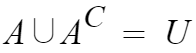
'A인것'과 'A가 아닌것'을 합집합하면 당연히 전체집합이 나온다.
11. A와 A의 여집합의 교집합은 공집합이다.
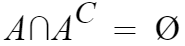
A이면서 A가 아닌것? 당연히 그런건 존재하지 않으니 공집합이다.
12. A에 대한 B의 차집합은 A와 B의 여집합의 교집합이다. (중요)
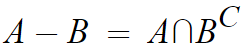
이게 그나마 가장 어려운거고 중요한거니까, 두가지 방법으로 설명해주겠다.
1. 논리적인 설명
A - B = A인데 B가 아닌것
A∩B^c = A 이면서 B가 아닌것
따라서 둘은 같다.
2. 벤 다이어그램으로 설명
A - B의 벤다이어그램을 그려보겠다.
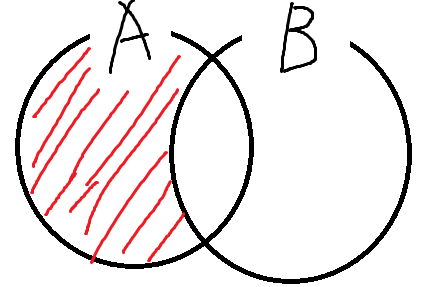
다음으로 A∩B^c의 벤다이어그램을 그려보겠다.

똑같다. 그래서 A에 대한 B의 차집합은 A와 B의 여집합의 교집합과 같다.
성질이 12개나 되지만
사실 다 딱보고 끄덕끄덕 할정도로 쉬운거고
그나마 마지막께 좀 어려울수 있고 중요한거니까 조금 강조해줬다.
- 드모르간의 법칙 -
얘도 중요한데 조금 어려우니 벤다이어그램을 그려주겠다.
1. A와 B의 합집합의 여집합은 A의 여집합과 B의 여집합의 교집합이다.
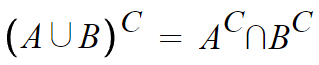
글로 풀어쓰려니 난리가났는데, 두가지 방법으로 설명해주겠다.
1. 논리적인 설명
A와 B의 합집합 = A이거나 B인것
따라서, A와 B의 합집합의 여집합 = A도 아니고, B도 아닌것
A의 여집합 = A가 아닌것
B의 여집합 = B가 아닌것
따라서, A의 여집합과 B의 여집합의 교집합 = A도 아니고, B도 아닌것
2. 벤다이어그램
A와 B의 합집합부터 그려보면
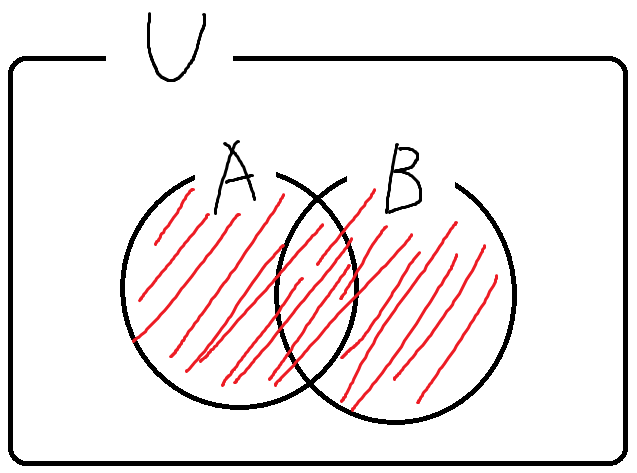
따라서, A와 B의 합집합의 여집합은

이번엔 A의 여집합을 그려보겠다.

A의 여집합이니 A 빼고 다 칠한다.
다음으로 B의 여집합을 그려보면
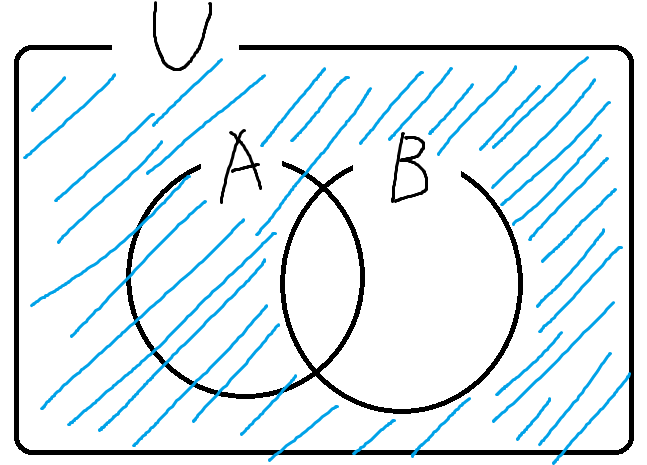
따라서 A의 여집합과 B의 여집합의 교집합은
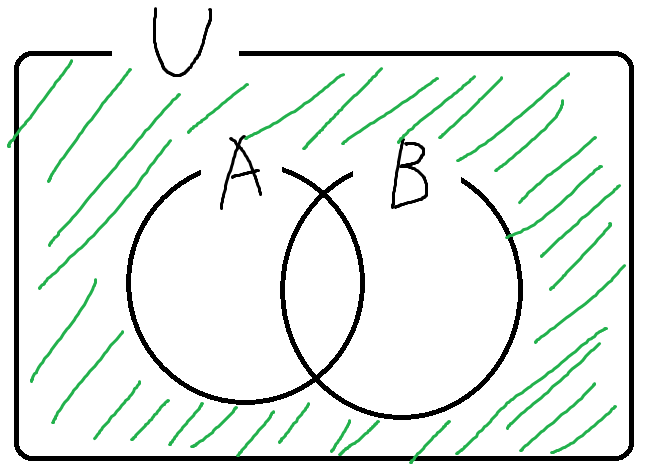
2. A와 B의 교집합의 여집합은 A의 여집합과 B의 여집합의 합집합이다.
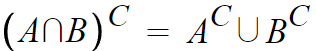
1. 논리적인 설명
A와 B의 교집합 = A이면서 B인것
따라서 A와 B의 교집합의 여집합 = A가 아니거나, B가 아닌것
A의 여집합 = A가 아닌것
B의 여집합 = B가 아닌것
따라서 A의 여집합과 B의 여집합의 합집합 = A가 아니거나, B가 아닌것
2. 벤다이어그램
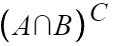
이것의 벤다이어그램을 그려보면
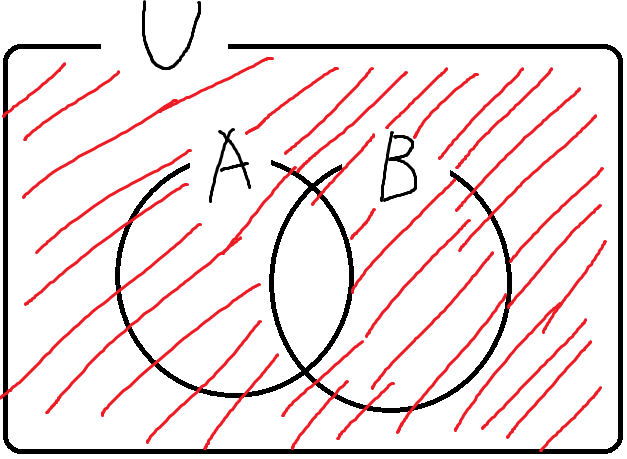

다음으로 이것의 벤다이어그램을 그려보면
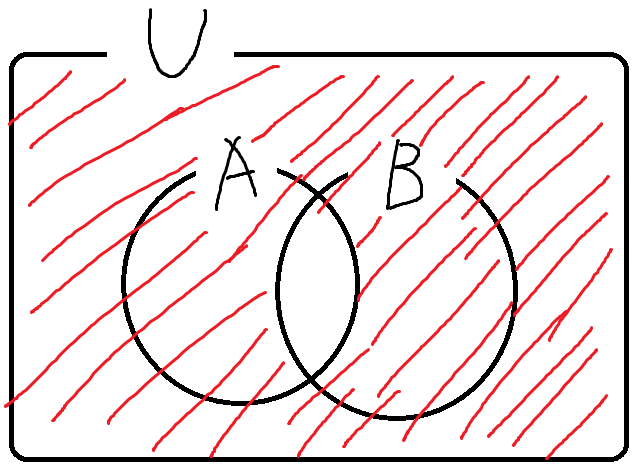
- 유한집합의 원소의 개수 -
왜 유한집합만 하냐면
무한집합이면 원소가 무한히 많은거라 개수를 논하는것 자체가 불가능하다.
이것도 벤다이어그램을 이용하면 된다.
어떻게 될지 생각을 해보면서 풀면 다 풀린다.
전체집합 U의 두 부분집합 A, B에 대하여
아래 식들이 성립한다.
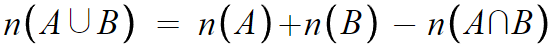
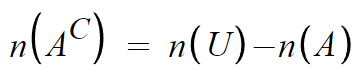
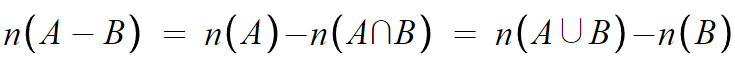
혹시 n(A)가 무슨말인지 모르나?
n(A) = 집합 A의 원소의 개수
셋다 조금만 생각해보면 너무 당연한거라
증명은 내가 다루지 않겠다. 직접 해보기바란다.
솔직히 귀찮아서 그러는거아니냐 할수있는데, 그게 맞다...
첫번째 식만 조금 설명해주겠다.
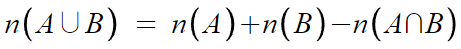
n(A∪B) 는 A와 B의 합집합의 원소의 개수이다.
이걸 구하려면, 일단 A와 B의 원소의 개수를 더해준다.
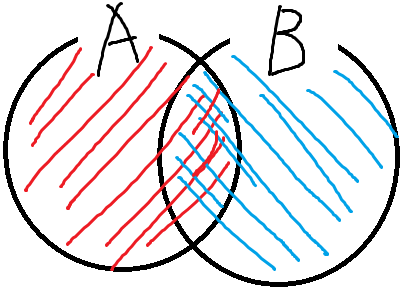
그러면, 보는것과 같이
A와 B의 교집합 부분이 두번 더해졌음을 알 수 있다.
두번 더해졌으면 한번 빼주면 되는거다.
그래서 이런 식이 탄생한것이다.
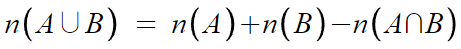
대충 어떤식으로 생각해야되는지 길을 알려줬으니,
여러분은 그 길을 따라 걷기만 하면 된다.
- 예제 -
1 )

답은 ㄱ, ㄷ, ㅁ 이다.
ㄱ )
A가 U의 부분집합이므로
A와 U의 교집합은 A이다.
따라서 ㄱ(o)
ㄴ )
A가 U의 부분집합이므로
A와 U의 합집합은 U이다.
따라서 ㄴ(x)
ㄷ )
어떤 집합과 공집합의 교집합은 무조건 공집합이다.
따라서 ㄷ(o)
ㄹ )
공집합은 아무것도 없는 집합이라
빼든 안빼든 아무 변화가 없다.
따라서 U-Ø=U 이다.
따라서 ㄹ(x)
ㅁ )
A가 U의 부분집합인데,
U가 전체집합이니까
U-A = U인데 A는 아닌것
즉 A의 여집합이다.
따라서 ㅁ(o)
공식 이용해도 된다.
U-A = U∩A^c = A^c 이다.
따라서 답은 ㄱ, ㄷ, ㅁ
2 )
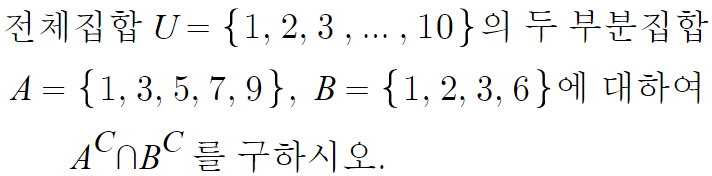
답은 {4, 8, 10} 이다.
1. 논리적인 풀이
A의 여집합과 B의 여집합의 교집합을 구하란다.
따라서 구하고자 하는것은,
A가 아니면서 B도 아닌것이다.
즉 1 3 5 7 9 아니고 1 2 3 6 아닌것만 모으면 된다.
그런 원소는 4, 8, 10 이고
따라서 답은 {4, 8, 10} 이다.
2. 벤다이어그램 풀이
우리가 구하고자 하는것을 벤다이어그램으로 그리면
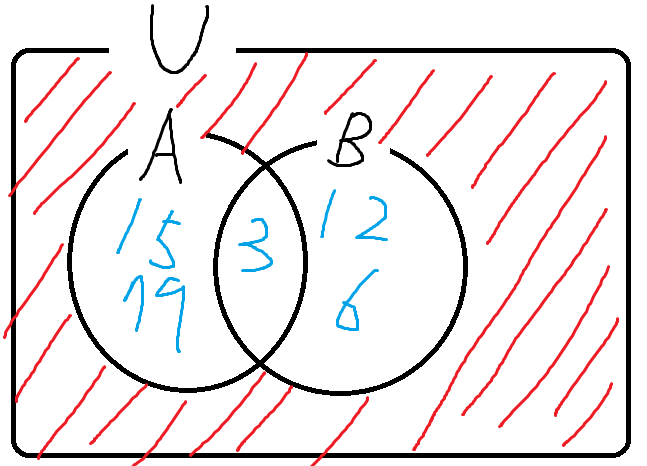
색칠되는것에 해당하는 원소는 4, 8, 10 이다.
따라서 답은 {4, 8, 10} 이다.
3. 공식풀이(드모르간법칙)
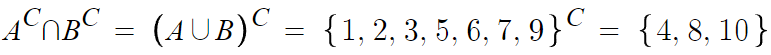
따라서 답은 {4, 8, 10} 이다.
3 )
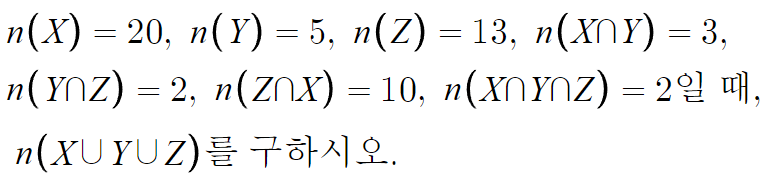
답은 25이다.
이렇게 복잡한 문제는 벤다이어그램이 가장 쉽다.
그냥 벤다이어그램은 무적이다.
1. 논리적인 풀이
n(X∪Y∪Z)를 구하려면
n(X)+n(Y)+n(Z)를 해준 뒤
중복해서 여러번 더해진걸 다시 빼주면 된다.
X∩Y와 Y∩Z와 Z∩X는 각각 두번씩 더해졌으므로
한번씩 빼준다. 여기까지 하면
n(X)+n(Y)+n(Z) - n(X∩Y) - n(Y∩Z) - n(Z∩X)
근데 아직 끝나지 않았다.
왜냐면 X∩Y∩Z는 세번 더해질거라 두번만 빼주면 되는데
아까 빼는것때문에 세번이나 빼졌기 때문이다.
따라서 얘는 여기다가 또 더해줘야한다.
n(X)+n(Y)+n(Z) - n(X∩Y) - n(Y∩Z) - n(Z∩X) + n(X∩Y∩Z)
문제에서 준 조건을 이용해 대입하여 계산하면
답은 25이다.
2. 벤다이어그램 풀이
그냥 얘가 압도적으로 쉽다.
벤다이어그램을 그려보겠다.
적힌 숫자는 각 영역에 해당하는 원소의 개수를 의미한다.
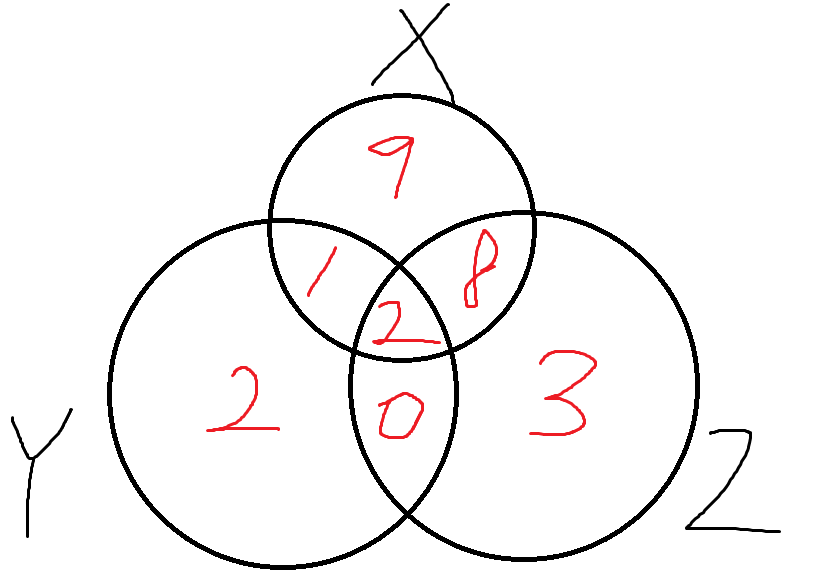
따라서 답은 각 영역을 다 더한것
9+1+2+8+2+0+3 = 25 이다.
'수학(하) > I. 집합과 명제' 카테고리의 다른 글
| 명제 #2 - 조건과 진리집합, 부정 (0) | 2022.05.07 |
|---|---|
| 명제 #1 - 명제란 무엇인가? (0) | 2022.04.28 |
| 집합 #4 - 여러가지 집합 (0) | 2022.04.07 |
| 집합 #3 - 부분집합 (0) | 2022.04.07 |
| 집합 #2 - 집합의 원소의 개수와 여러가지 집합 (0) | 2022.04.03 |



