
- 개요 -
집합의 정의에 대한 이해를 바탕으로
본격적으로 집합을 다루기 시작한다.
그중에서 이번에 다룰 주제는 '부분집합'이다.
- 부분집합의 정의 -
두 집합 A, B에 대하여
A의 모든 원소가 B에 속할 때,
A를 B의 부분집합이라 한다.
좀 쉽게 설명하자면,
A = {1, 2} 이고
B = {1, 2, 3, 4} 이다.
A의 원소는 1, 2 이고
1, 2는 둘다 집합 B의 원소로 속해있으므로
A는 B의 부분집합이다.
A라는 집합은 B라는 집합의 일부분이다. 정도로 이해하면 된다.
하나만 더 예를 들어보자면
A = { x | x는 자연수 }
B = { x | x는 양수인 짝수 }
이렇게 두 집합이 있다고 해보자.
양수인 짝수는 모두 자연수이다.
따라서 B는 A의 부분집합이다.
하지만, 모든 자연수가 짝수인건 아니다.
따라서 A는 B의 부분집합이라 할수 없다.
이해를 돕기 위해서,
A가 B의 부분집합임을 벤다이어그램으로 표현하면 아래와 같다.

- 부분집합의 표현 -
부분집합도 표현하는 기호가 있는데,
∈랑 비슷하게생겨서 헷갈리기 쉬우니 조심하자.
부분집합은 아래의 기호로 표현한다.
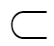
A가 B의 부분집합이다. 라는걸 표현하려면

이렇게 쓰면 된다.
반대로, A가 B의 부분집합이 아니다. 라는걸 표현하려면

이렇게 쓰면 된다.
외우는데 조금 도움을 주자면,
A⊂B 이 식은
뭔가 B가 A를 담고있다고 느껴지지 않는가?
그 느낌이 맞다. 잘 만든 기호이다.
- 부분집합의 성질 -
매우 중요한곳이다.
아주 당연한 말들이지만 막상 문제풀때는 잘 안떠오르니까
대충보면 안된다.
1 - 모든 집합은 자기 자신의 부분집합이다.
식으로 나타내면 아래와 같다.
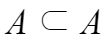
A라는 집합의 부분집합은 많이 있겠지만
확실한거 하나는, A도 A의 부분집합이다.
왜냐면, A의 모든 원소는 당연히 A에 속할거기 때문이다.
2 - 공집합은 모든 집합의 부분집합이다.

이것도 당연한거다.
공집합은 원소가 없는 집합이다.
따라서 공집합은 A가 무슨 집합이든 무조건 A의 부분집합이다.
3 - A⊂B이고 B⊂C이면 A⊂C이다.

이것도 논리적으로 당연한거다.
삼단논법과 비슷한거다.
모든 A가 B에 속하고
모든 B가 C에 속하면
당연히 모든 A는 C에 속할수밖에 없다.
예를 들자면,
A는 자연수의 집합이다.
B는 정수의 집합이다.
C는 실수의 집합이다.
그러면, 모든 자연수는 정수이다. A⊂B
모든 정수는 실수이다. B⊂C
따라서 모든 자연수는 실수이다. A⊂C
벤다이어그램을 그려보면 이해가 쉽다.
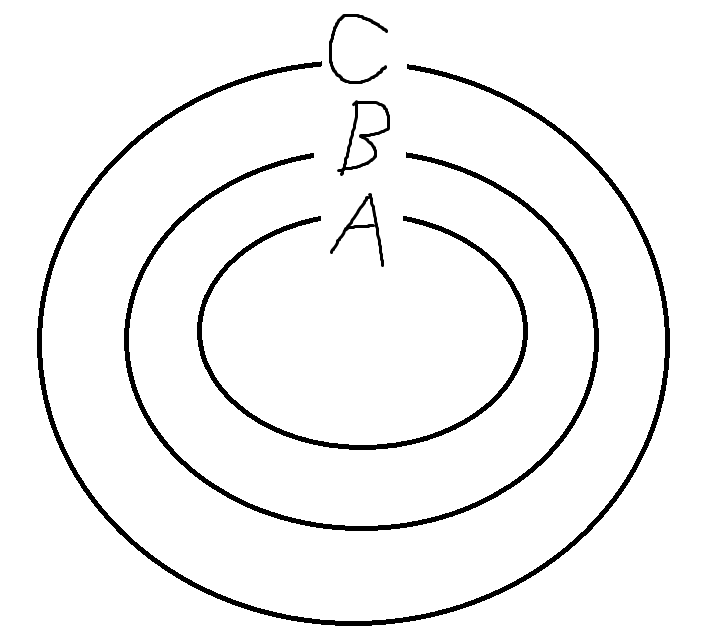
- 집합이 서로 같을 조건 -
집합 A = {2, 3, 4} 이고
집합 B = {2, 3, 4} 라고 해보자.
이러면 A와 B는 완전히 같은 집합이다.
원소가 다 똑같기때문이다.
그러면, 집합 B = {3, 2, 4}라고 하면
이것도 같은 집합인가?
같은 집합이다. 원소만 다 똑같다면 원소의 순서는 상관없다.
수학적인 표현으로, 두 집합 A, B가 서로 같을 조건은 아래와 같다.

즉, A가 B의 부분집합이면서
B가 A의 부분집합이면
A와 B는 완전히 같은 집합이다.
부분집합의 정의가 뭔가?
A의 모든원소가 B에 속했으니까 A⊂B 인거다.
그리고 B의 모든원소가 A에 속했으니까 B⊂A 인거다.
A의 모든원소가 B에 속하는데,
B의 모든원소가 A에 속한다고 한다.
이러려면 A와 B의 원소가 완전히 같을수밖에 없다.
벤다이어그램으로 그려보면 이해가 쉽다.
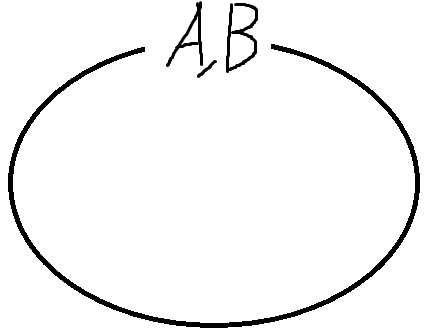
A가 B의 부분집합이면서
B가 A의 부분집합이려면
이렇게밖에 못그린다.
따라서 A와 B는 완전히 같아야한다.
집합 A와 B가 서로 같다는건 등호(=)로 표시하면 된다.
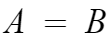
반대로 서로 같지 않다는건 ≠ 로 표시하면 된다.
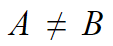
- 진부분집합 -
집합 B가 있다고 하자.
B의 부분집합중 B가 아닌것을 진부분집합이라 한다.
식으로 나타내면 아래와 같다.
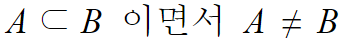
즉, 부분집합중 자기자신을 제외한건 다 진부분집합이다.
집합 {1, 2}의 진부분집합은?
Ø, {1}, {2} 이다.
{1, 2}는 부분집합이긴 하지만, 자기자신이기 때문에 진부분집합은 아니다.
- 부분집합의 개수 -
여긴 조금 어려우니 집중하자.
중학교때 경우의수 구하는걸 배웠을텐데, 그것의 응용이다.
집합 A가 있다고 해보자.
집합 A의 원소는 n개이다.
집합 A를 아래와 같이 표현할것이다.
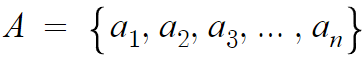
이 집합 A의 부분집합의 개수를 구해보자.
부분집합을 B라 하겠다.
그러고 A의 원소들에게 가서 물어볼것이다.
B에 들어갈거냐? 안들어갈거냐?
a₁이 나 들어갈래 했다면 B에 들어가는거고
안들어갈래 했다면 안들어가는거다.
a₁이 B에 들어가든 안들어가든 B가 A의 부분집합임은 반박할수 없는 사실이다.
즉, A의 1번째 원소인 a₁을 가지고 B를 구성하는 방법은 두가지이다.
이번엔 a₂에게 가서 똑같이 물어본다.
a₂가 나 들어갈래 했다면 B에 들어가는거고
안들어갈래 했다면 안들어가는거다.
즉, A의 2번째 원소인 a₂을 가지고 B를 구성하는 방법은 두가지이다.
이를 같은 방법으로 모든 원소에게 해주면
A의 3번째 원소인 a₃을 가지고 B를 구성하는 방법은 두가지이다.
A의 4번째 원소인 a₄를 가지고 B를 구성하는 방법은 두가지이다.
...
A의 n번째 원소인 a_n을 가지고 B를 구성하는 방법은 두가지이다.
하나의 원소를 가지고 B를 구성하는 경우의수가 2이고
이를 n개의 원소에게 했으므로
B를 구성하는 최종적인 경우의수는
곱의법칙 : 동시에 일어나는 사건들의 경우의수는 서로 곱한다.
따라서 2를 n번 곱한것, 즉 2ⁿ 이다.
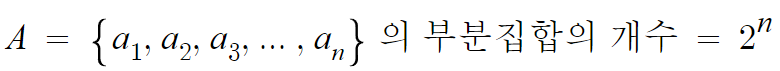
이를 좀더 간단히 쓰면, 다음과 같은 결론을 얻는다.

Q) A = {1, 1} 이면 A의 부분집합의 개수는 3개인데요?
A) 애초에 집합은 원소가 중복되어 나열되지 않는다. 원소는 서로 다른것들 이어야한다.
- 심화 : 특정한 원소 k개를 반드시 원소로 갖는 부분집합의 개수 -
예를 들자면, 이런 상황이다.
A = {1, 2, 3, 4}일때, 2를 원소로 갖는 부분집합의 개수는 몇개인가?
원소의 개수가 n개인 집합의 부분집합의 개수는 2ⁿ이다.
그럼 이 집합의 부분집합중에서
원소가 k개 이상인 것의 개수는?
이것도 아까 부분집합의 개수 처음 구할때처럼 하면 된다.
대신 이번에는
원소가 k개 이상이어야하므로
지목된 특정한 k개의 원소에겐 선택권이 없다.
넌 무조건 부분집합으로 들어가야한다. 라고
k개의 원소에게 당부해두는것이다.
그럼 최종적인 경우의 수는
n개의 원소에게 들어갈거냐 안들어갈거냐 묻는게 아니라
n-k개의 원소에게 물어볼거라
2를 n번 곱하는게 아니라
2를 n-k번 곱해야한다.
따라서 최종적인 경우의 수는
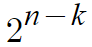
그럼 이번엔 반대로 특정한 원소 ℓ개 를 원소로 갖지 않는 것의 개수는?
이번에도 지목된 특정한 ℓ개의 원소에게는 선택권이 없다.
넌 부분집합으로 들어갈수 없다. 라고
ℓ개의 원소에게 당부해두는것이다.
따라서 이때 최종적인 경우의 수는
2를 n-ℓ번 곱하는것

- 예제 -
1 )
두 집합 X, Y의 관계를 기호 ⊂, =, ≠를 사용하여 나타내시오.
X = { x | x는 정사각형 }
Y = { y | y는 마름모 }
모든 정사각형은 마름모이다.
따라서 X⊂Y이다.
그런데, 모든 마름모가 정사각형인건 아니다.
따라서 Y⊂X 라고는 쓸수없다. 따라서 X≠Y 이다.
따라서 답은 X⊂Y, X≠Y이다.
2 )

답은 ㄱ 이다.
ㄱ )
2는 20 이하의 소수이므로 ㄱ(o)
ㄴ )
23은 소수이긴 한데 20 이하가 아니기때문에
A에 속할수 없다. 따라서 ㄴ(x)
ㄷ )
이건 내가 함정을 파놨다. 많이 속았을거라 생각한다.
∈ 기호는 원소가 집합에 포함되었다는걸 나타내는 기호이다.
Ø는 원소가 아니라, 이거 자체로 '공집합' 이라는 이름의 엄연한 집합이다.
따라서 Ø∈A 라고 쓸게 아니라, Ø⊂A 라고 썼어야한다.
따라서 ㄷ(x)
ㄹ )
4는 소수가 아니기때문에
4를 원소로 가진 집합 {4, 15}는 A의 부분집합이 될 수 없다.
따라서 ㄹ(x)
ㅁ )
이것도 많이틀렸을거같은데
1은 소수가 아니다.
따라서 ㅁ(x)
따라서 답은 ㄱ
여기서 틀려놓고 이런 변명을 할수 있다.
옳은거 있는대로 고르라더니 답이 한개인건 억지아닌가요?
좀 억지는 맞는데, 아무튼 있는대로 고른건 맞지않나? 난 두개 고르라고 한적이 없다.
본인이 확실히 알고있다면, 틀린 선지를 고를게 아니라 문제의 억지스러운 표현을 의심했어야했다.
3 )
집합 A = {1, 2, 3, 4, 5}의 부분집합 중
2를 반드시 원소로 갖는 집합의 개수는?
우선 A는 원소가 5개이므로
A의 부분집합의 개수는 2^5 = 32개이다.
하지만 문제에서 묻는건 이게 아니다.
부분집합중 2를 원소로 갖는걸 구하란다.
부분집합의 개수를 어떻게 구했었는지 되새겨보자.
원소들에게 찾아가서 부분집합에 들어갈지 안들어갈지 물어봤었다.
그런식으로 하면 된다.
대신 2에게는 선택권이 없다. 2는 무조건 부분집합에 들어와야한다.
따라서 1, 3, 4, 5에게만 물어보면 된다.
따라서 4개의 원소를 가지고 부분집합을 짤것이므로
최종적인 경우의수는 2⁴ = 16
따라서 답은 16
'수학(하) > I. 집합과 명제' 카테고리의 다른 글
| 명제 #1 - 명제란 무엇인가? (0) | 2022.04.28 |
|---|---|
| 집합 #5 - 집합의 연산 (0) | 2022.04.15 |
| 집합 #4 - 여러가지 집합 (0) | 2022.04.07 |
| 집합 #2 - 집합의 원소의 개수와 여러가지 집합 (0) | 2022.04.03 |
| 집합 #1 - 집합의 뜻과 표현 (0) | 2022.04.01 |



