
- 개요 -
여러가지의 새로운 집합 개념이 들어온다.
내용이 조금 많고 헷갈리기 쉽다.
핵심 : 이해가 잘 안되면 벤다이어그램을 그려봐라.
여기는 문제를 풀어보면서 오개념을 잡는게 효율적이다.
- 합집합과 교집합 -
두 집합 A, B에 대하여
A에 속하거나 B에 속하는 원소들로 이루어진 집합을
A와 B의 합집합이라 한다.
즉, A와 B의 원소를 모두 모은게 합집합이다.
예를 들자면, A = {1, 2, 3} 이고
B = {3, 4, 5} 이다.
그럼 A와 B의 합집합은 {1, 2, 3, 4, 5} 인 것이다.
A와 B의 합집합은 식으로 아래와 같이 나타낸다.

∪ 라는 기호를 쓴다.
이것도 기호를 잘 만들어놓은게, A∪B 라고 써놓으면
∪ 이 기호가 A와 B를 담을거같이 생기지 않았나?
A와 B의 합집합은 벤다이어그램으로 아래와 같이 나타낸다.

주의할건, 합집합이라고 A+B 이렇게 표현하면 안된다.
- 다음으로 교집합 -
두 집합 A, B에 대하여
A에도 속하고, B에도 속하는 원소들로 이루어진 집합을
A와 B의 교집합이라 한다.
즉, A와 B에 둘다 포함되는 원소를 모두 모은걸 교집합이라 한다.
예를 들자면, A = {1, 2, 3} 이고
B = {3, 4, 5} 이다.
그럼 A와 B의 교집합은 {3} 인 것이다.
A와 B의 교집합은 식으로 아래와 같이 나타낸다.

∩ 라는 기호를 쓴다.
A와 B의 교집합은 벤다이어그램으로 아래와 같이 나타낸다.

색칠한것만 교집합이다.
'교점' 이라는게 '만나는 점' 이라는 뜻이니까
교집합도 둘의 공통부분이라고 이해하면 된다.
- 두줄요약 -
합집합 : A or B . A∪B
교집합 : A and B . A∩B
- 집합에서의 서로소 -
우선, 중1때 배웠던 서로소의 개념을 되새겨보자.
두 자연수가 서로소라는건, 두 자연수의 최대공약수가 1이라는 것이다.
즉 1을 제외한 공약수가 없다.
집합에서의 서로소도 비슷한 맥락이다.
집합 A, B가 있는데
두 집합이 공통부분이 없다면 A와 B는 서로소이다.
즉, A와 B의 교집합이 공집합이면 서로소이다.
식으로 나타내면 A∩B = Ø
이것도 벤다이어그램으로 나타내보면

A와 B는 공통부분이 없기때문에
둘은 완전히 따로논다.
- 전체집합 -
다음 내용이 '여집합'과 '차집합'이다.
여집합과 차집합을 다루기 전에 '전체집합' 이라는걸 먼저 다뤄야한다.
전체집합 : 말 그대로 전체를 나타내는 집합.
어떤 집합에 대해서 그것의 부분집합을 다룰때,
그 처음의 집합을 전체집합이라 한다.
보통 전체집합의 이름은 U 라고 짓는다.
이 전체집합은 실수 전체의 집합이 될수도 있고,
8보다 작은 자연수의 집합이 될수도 있고,
출제자 마음대로이다.
전체집합을 U라고 이름지은 이유는
전체집합이 영어로 Universal set 라서 그렇다.
- 여집합 -
전체집합을 U = { x | x는 8 이하의 자연수 }
라 하겠다.
이때, 집합 A를 A = {3, 4, 5} 라 하면
A는 U의 부분집합이다.
그런데, U에는 속하지만 A에는 아예 속하지 않는 집합도 있을거아닌가?
{1, 2, 6, 7, 8} 이 그렇다.
이건 U의 부분집합이지만, 아무것도 A에 속하지 않는다.
이런걸 A의 여집합이라 한다.
즉, 전체집합 U에 속하지만, A에는 속하지 않는 원소를 모은게 A의 여집합이다.
이를 A^C 라 표현하며, 식으로 나타내면 아래와 같다.

벤다이어그램으로 나타내면 아래와 같다.

U에는 속하지만, A에는 속하지 않는것이다.
왜 이름이 여집합이냐면
여집합의 '여'는 餘(남을 여) 이다.
남는시간을 여가시간이라 부르는것과 같은 느낌이다.
U에서 A를 뽑아내고 남는게 바로 여집합인 것이다.
A^C에서 C는 어디서 온거냐면
여집합이 영어로 complement set라서 그렇다.
- 차집합 -
두 집합 A, B에 대하여
A에는 속하지만, B에는 속하지 않는 원소를 모은것을
A에 대한 B의 차집합 이라고 한다.
즉, A인데 B는아닌것 을 A에 대한 B의 차집합 이라고 한다.
기호로는 A-B 로 나타내며, 식으로 나타내면 아래와 같다.

이것도 벤다이어그램을 그려보면 이해가 쉽다.
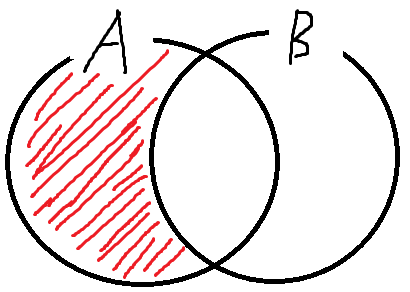
여집합과 비슷하긴 한데, 헷갈리면 안된다.
B의 여집합은 : 전체집합에서 B를 뗀거고
A에 대한 B의 차집합은 : A에서 B를 뗀거다.
그럼 U에 대한 B의 차집합은?
U 에서 B를 뗀것.
따라서, 다음과 같은 결론을 얻는다.
U - B 는 B의 여집합이다.
- 간단요약 -
A와 B의 합집합 : A or B : A∪B
A와 B의 교집합 : A and B : A∩B
A의 여집합 : not A : A^C
A에 대한 B의 차집합 : A but not B : A-B
전체집합 U : All(Origin)
- 집합의 연산법칙 -
다항식의 연산법칙과 똑같다.
집합을 연산할때 다항식 연산할때처럼 취급해도 된다는뜻이다.
다항식처럼 교환법칙, 결합법칙, 분배법칙이 성립한다.

주의할건, 합집합과 교집합에 대해서만 성립하는 법칙이다.
내 개인적인 생각은, 그냥 이런거 쓰지말고 벤다이어그램으로 풀어라.
벤다이어그램 그려보면 너무 당연한것임을 알 수 있다.
헷갈릴거같다? 그러면 그냥 벤다이어그램 그려서 풀어라.
나도 벤다이어그램 그려서 푼다.
직관적인 그림이 이해가 쉬운건 사실이고, 굳이 어려운 길로 갈 필요 없다.
- 예제 -
1 )
다음 두 집합 A, B에 대하여 A∪B를 구하시오.
A = {a, b, c}, B = {b, d, e}
A와 B의 합집합을 구하라는 뜻이다.
A와 B의 합집합 = A or B
따라서 A와 B의 합집합은
{a, b, c, d, e} 이다.
벤다이어그램을 그리면 이해가 더 쉽다.

따라서 답은 {a, b, c, d, e}
2 )
다음 두 집합 A, B에 대하여 A∩B를 구하시오.
A = {x|2≤x<12}, B = {x|x≥7}
A와 B의 교집합을 구하라는거다.
이 문제는 x가 딱딱 정수로 떨어지는 수가 아니라
범위로 주어졌기때문에
벤다이어그램으로는 못푼다.
교집합이 뭔지만 알면 풀수있다.
A와 B의 교집합 = A and B
A and B인건 뭔가?
7≤x<12 인 부분이다.
따라서 답은 {x|7≤x<12}
참고로, 정확히 이런 집합 표현식으로 적어야한다.
3 )
두 집합 A, B에 대하여
A = {1, 3, 5}, A∩B = {3}, A∪B = {1, 2, 3, 4, 5}
일 때, 집합 B를 구하시오.
1 : 합집합과 교집합의 정의를 이용한 풀이
A가 {1, 3, 5} 인데
A와 B의 교집합이 {3} 이므로
B엔 1과 5가 들어가지 않으며, 3이 들어가야한다.
그리고 A와 B의 합집합이 {1, 2, 3, 4, 5} 이므로
B엔 A에 없는 2, 4가 들어가야한다.
따라서 B = {2, 3, 4}
2 : 벤다이어그램을 이용한 풀이
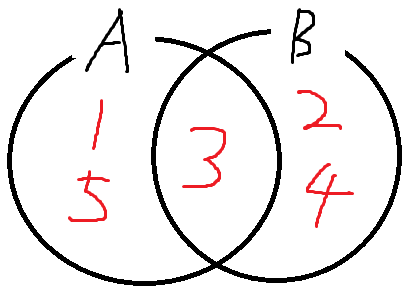
따라서 B = {2, 3, 4} 이다.
4 )

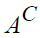
이것부터 구해보자.
A의 여집합이라는 뜻이다.
A의 여집합 = not A
따라서 A의 여집합은 {1, 2, 4}를 제외한 모두이다.
따라서 A의 여집합은 {3, 5, 6, 7, 8, 9} 이다.
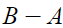
다음으로 이걸 구해보자.
B에 대한 A의 차집합이라는 뜻이다.
B-A = B but not A
따라서 B-A는 B={2,5,6,7} 에서
A에도 해당되는 2를 없애줘야한다.
따라서 B-A = {5, 6, 7}
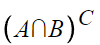
마지막으로 이걸 구해보자.
A와 B의 교집합의 여집합 이라는 뜻이다.
글로 풀어써서 어려워보이는거지만, 벤다이어그램으로 보면 쉽다.
A와 B의 교집합은 {2} 이다.
{2}의 여집합은 {1, 3, 4, 5, 6, 7, 8, 9} 이다.
따라서 A와 B의 교집합의 여집합은 {1, 3, 4, 5, 6, 7, 8, 9} 이다.
'수학(하) > I. 집합과 명제' 카테고리의 다른 글
| 명제 #1 - 명제란 무엇인가? (0) | 2022.04.28 |
|---|---|
| 집합 #5 - 집합의 연산 (0) | 2022.04.15 |
| 집합 #3 - 부분집합 (0) | 2022.04.07 |
| 집합 #2 - 집합의 원소의 개수와 여러가지 집합 (0) | 2022.04.03 |
| 집합 #1 - 집합의 뜻과 표현 (0) | 2022.04.01 |



