
- 확률의 수학적 정의 -
어떤 일이 일어날 가능성을 수치로 나타낸것인데
이건 일상적인 표현이고
수학적으로 표현할줄 알아야한다.
어떤 일이라는건 뭘 말하는거고
그 수치로 나타내는 방법은 또 뭔지를 공부하는 곳이다.
확률, probability
표본공간 S의 각각의 원소가 일어날 가능성이 같은 정도로 기대될 때,
표본공간 S의 원소의 개수 n(S)와 사건 A의 원소의 개수 n(A)에 대하여
사건 A가 일어날 확률 P(A)를 다음과 같이 나타낸다.
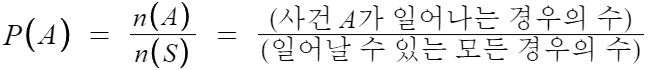
표본공간은 뭐고 원소가 일어난다는건 무슨말이고
갑자기 분수는 왜나오고 당황스러울텐데
용어 설명과 함께
조금 쉽게 설명해줄 필요가 있다.
하나씩 보자. 표본공간 S 라는건 무슨말인가?
표본이 있는 공간 이라고 이해하면 된다.
예를 들어서 주사위를 던졌다고 하자.
여기서 나올수 있는 눈은
1, 2, 3, 4, 5, 6 이다.
여기서 '주사위를 던진다' 라는 '시행' 을 한것이고
그 '결과'로서 나올수 있는 눈은 1, 2, 3, 4, 5, 6 이다.
즉 주사위를 1회 던지는 시행에서
나올수 있는 눈의 경우를 전부 모으면 1, 2, 3, 4, 5, 6 이라는것이다.
여기서 이 1, 2, 3, 4, 5, 6은
이 주사위를 던진다는 시행에서 나오는 결과값이다.
여기서 이 결과값을 각각 원소로 해서 전부 모은 집합을 '표본공간' 이라 한다.
즉 주사위를 1회 던지는 시행에서의 표본공간 S = {1, 2, 3, 4, 5, 6} 이다.
요약하자면
어떤 '시행'에서 나올수 있는 '결과'를 각각 원소로 하여 '모두 모은 집합'을 '표본공간' 이라고 한다.
즉 표본공간은 곧 집합이다.
다른 예로, 동전을 한번 던진다고 해보자.
나올수 있는건 앞면, 뒷면이다.
따라서 동전을 한번 던진다는 '시행'에 대한 표본공간은
앞면, 뒷면을 각각 원소로 해서 전부 모은 집합인
S = {앞면, 뒷면} 이 되는것이다.
확률이란, 표본공간 S의 각각의 원소가 일어날 가능성이 어쩌고..
여기서 '표본공간 S의 각각의 원소' 가 무슨말인지는 해석이 완료되었다.
확률이란, 표본공간 S의 각각의 원소가 일어날 가능성이 같은 정도로 기대될 때 어쩌고...
그럼 여기서 각각의 원소가 일어날 가능성이 같은 정도로 기대된다는건 무슨말인가?
내가 지금부터 말도안되는 소리를 해보겠다.
주사위를 1번 던졌을때 6이 나올 확률은 50%이다.
왜냐? 6이 나오거나, 6이 나오지 않거나 두가지 경우 뿐이기때문이다.
뭔가 말도안되는 소리라는건 알겠는데
수학적으로 반박하기는 좀 곤란하지 않은가?
이를 반박하는게
'각각의 원소가 일어날 가능성이 같은 정도로 기대될 때'
라는 말로 설명하는거다.
6이 나오거나, 6이 나오지 않거나 두가지 경우인건 맞다.
근데 6이 나올 확률과
6이 나오지 않을 확률은 같지 않다.
실제로 6이 나올 확률은 1/6 이다.
6이 나오거나, 6이 나오지 않거나 하는 두가지 경우로 나눈다음
확률이 50%라 우길거면
표본공간에서의 각각의 원소
{6이 나옴, 6이 안나옴} 가 일어날 가능성이 같아야 한다는것이다.
근데 같지 않다.
왜냐면 6이 나오는 경우는 말그대로 6이고
6이 안나오는 경우는 1,2,3,4,5 중 하나가 나왔다는 것이기 때문이다.
따라서 주사위를 1번 던지는 '시행'을 할때
'표본공간'을 { 6이 나옴, 6이 안나옴 } 으로 잡아버리면
각각의 원소 '6이 나옴', '6이 안나옴' 이 일어날 가능성이 같지 않기때문에
이런식으로 6이 나올 확률을 구하려하면 안된다는것이다.
즉 표본공간의 원소는 일어날 가능성이 같은 것들로 구성해야한다.
그러지 않으면 위와 같은 말도안되는 논리가 나오는것이다.
그럼 이제 아래 문장이 해석 가능하다.
확률이란, 표본공간 S의 각각의 원소가 일어날 가능성이 같은 정도로 기대될 때 어쩌고...
이는 해석하자면
어떤 시행에 대해 나올수 있는 경우를 원소로 하여 모두 모은 집합이 표본공간 S인데
이 표본공간 S의 각각의 원소가 일어날 가능성이 같아야한다. 라는 말이다.
이제 두줄만 해석하면 된다.
확률이란, 표본공간 S의 각각의 원소가 일어날 가능성이 같은 정도로 기대될 때,
표본공간 S의 원소의 개수 n(S)와 사건 A의 원소의 개수 n(A)에 대하여
사건 A가 일어날 확률 P(A)를 어쩌고...
우선 첫번째줄은 무슨말인지 알았고
첫번째줄을 무난히 따라왔다면 두번째줄은 금방 할수 있다.
표본공간 S는 집합이다.
집합 S의 원소의 개수는 n(S)이다.
이제 사건 A의 원소의 개수 n(A)가 무슨말인지 해석하면 된다.
'사건' 이라는 것의 수학적 정의는 '표본공간의 부분집합'이다.
즉 사건도 집합이다.
좀 쉽게 설명하자면
어떤 시행에서 나올수 있는 모든 경우를 모은게 표본공간이니까
어떤 시행에서 나오는 사건은 무조건 표본공간 안에서 일어날수밖에 없다.
예를 들어서, 주사위를 1번 던지는 시행에서 나오는 주사위 눈의 표본공간은 {1, 2, 3, 4, 5, 6} 이다.
여기서 3 이하의 수가 나오는 사건을 A라 하겠다.
그럼 A는 주사위의 눈이 1, 2, 3 인 경우를 말하는거고
이를 집합으로 표현해서 A = {1, 2, 3} 이라 표현한다는거다.
그리고 사건 A가 표본공간 S의 부분집합이므로
사건 A에서 각 원소가 일어날 확률도 각각 똑같을것이다.
실제로 주사위에서 1이 나올 확률, 2가 나올 확률, 3이 나올 확률은 같다.
그리고 여기서 주사위의 각 눈이 나올 확률이 같다는것에 대한 반박은 받지 않는다.
물론 던질때의 힘, 공기저항, 바닥과의 충돌 등 여러가지를 물리적으로 아주 정밀하게 계산하여 섬세하게 던지면
계속 6만 나오게 한다던가 하는 묘기가 가능하다.
하지만 그런건 사람이 할수있는게 아니기때문에 생각하지 않는거다.
이제 한줄남았다.
표본공간 S의 각각의 원소가 일어날 가능성이 같은 정도로 기대될 때,
표본공간 S의 원소의 개수 n(S)와 사건 A의 원소의 개수 n(A)에 대하여
사건 A가 일어날 확률 P(A)를 다음과 같이 나타낸다.
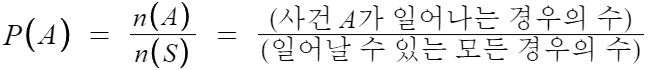
사실 너무 당연한말이라 위의 두줄만 이해했다면 바로 이해될것이다.
S는 표본공간, 즉 전체 경우를 담고있는 집합이기 때문에
집합 S의 원소의 개수 n(S)는 곧 어떤 시행에 대한 전체 경우의 수가 된다.
예를 들어, 주사위를 한번 던지는 '시행'에서
표본공간 S = {1, 2, 3, 4, 5, 6} 이고
따라서 n(S) = 6 이다.
주사위의 눈의 개수가 6개니까 일어날수 있는 모든 경우의 수가 맞다.
그리고 사건 A가 일어날 확률을 P(A)라 한다고 한다.
P는 확률이 영어로 probability니까 첫글자인 p를 따온거라 이해하면 된다.
P(A) = A라는 사건이 일어날 확률
함수 f(x)와 비슷한 느낌이다. x값에 따라 f(x)값이 정해지는것처럼
사건 A가 무엇이냐에 따라 P(A)값이 정해진다.
그리고 추가로, 주사위에서 7의 눈이 나오는건 있을수 없는일이다.
이처럼 '절대로 일어날수 없는 사건'을 공사건이라 하고, 표현하는 기호는 Ø 이다.
이제 확률이 뭔지 수학적으로 설명하라하면 설명할수 있다.
어떤 사건이 일어날 확률이란,
어떤 시행에 대해서 그 사건이 일어날 수 있는 경우의 수를
그 시행에 대해서 일어날 수 있는 모든 경우의 수로 나눈것이다.
단, 각각의 경우가 일어날 가능성은 같다.
확률의 정의가 세줄밖에 안되는데
이를 설명하려고 50줄정도는 쓴거같다.
하지만 전혀 과하다 생각하지 않는다.
확률의 정의를 정확히 이해하고 들어가지 않으면
나중에 문제풀다가
이상한 오개념에 자기가 빠져서 빠져나오지 못하게된다.
본인이 확률을 처음 공부할때
확률이 그냥 확률이지 하고 안읽고 그대로 문제풀다가
한번 제대로 오개념에 빠져서 고생한적이 있다.
- 확률의 기본 성질 -
당연한것들만 적혀있지만 중요하다.
1. 임의의 사건 A에 대하여 0≤P(A)≤1 이다.
2. 표본공간 S에 대하여 P(S)=1 이다.
3. 공사건 Ø에 대하여 P(Ø)=0 이다.
하나씩 증명해보자면

P(A)가 이건데
A는 S의 부분집합이고
공집합이 A의 부분집합이므로
아래 식이 성립한다.

따라서 아래 식이 성립한다.

n(Ø)=0 이므로 다시 쓰면

그리고 이것을 각각 n(S)로 나눠주면

따라서 첫번째 성질이 증명 완료되었다.
두번째것도 같은 방식으로 증명된다.
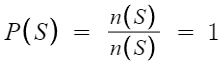
세번째것도 같은 방식으로 증명된다.

- 예제 -

양 끝 모두에 A가 적힌 카드가 나오게 나열되는 사건을 X라 하겠다.
그럼 확률은
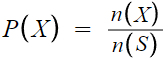
즉 사건 X의 경우의 수와
전체 경우의 수를 구하면 되는거다.
따라서 확률문제는 경우의 수를 두번 구해야된다.
1. 전체 경우의 수
2. 특정 조건을 만족하는 사건의 경우의 수
전체 경우의수부터 구해보자.
A, A, A, B, B, C 를 모두 한번씩 사용하여 임의로 일렬로 나열한다한다.
이것의 경우의 수는
우선 C를 6자리중 하나에 배열시킨다. 이것의 경우의수는 6
다음 A 3개를 5자리에 배열시킨다.
A끼리는 구별이 안되기때문에 A가 들어갈 자리를 '선택'만 하면 된다.
따라서 A 3개를 배열시키는 경우의 수는
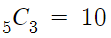
그리고 남은건 B 두개에 자리 두자리인데
B끼리는 구별이 안되기때문에 B가 들어갈 자리만 뽑으면 된다.
근데 남는자리가 두자리 뿐이라 선택권없이
B 2개를 배열시키는 경우의 수는 1
따라서 전체 경우의 수는 6×10×1 = 60
다음으로 양 끝 모두에 A가 적힌 카드가 나오게 나열되는 경우의 수는
일단 A를 양끝에 배열시킨다음 나머지를 배열시키는 방향으로 생각해보자.
A를 양끝에 배열시키는 경우의 수는
A끼리는 구별이 안되기때문에
그냥 똑같은 A 3개중에 아무거나 2개를 양끝에 놓으면 된다.
따라서 A를 양끝에 배열시키는 경우의 수는 1이다.
그러면 남은건 A, B, B, C이고 남은 자리는 4자리이다.
이를 배열하는 경우의 수는
A가 들어갈수 있는 자리는 4자리니까 4
C가 들어갈수 있는 자리는 3자리니까 3
나머지 B 두개는 선택권없이 남는데 가야하므로 1
따라서 양 끝 모두에 A가 적힌 카드가 나오게 나열되는 경우의 수는
1×4×3×1 = 12
따라서 구하고자 하는 확률 P(X)는
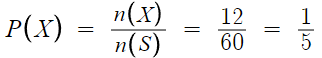
따라서 답은 2번
'확률과 통계 > II. 확률' 카테고리의 다른 글
| 독립시행 #2 - 독립시행의 확률 (0) | 2021.12.08 |
|---|---|
| 독립시행 #1 - 독립사건과 종속사건 (0) | 2021.12.07 |
| 조건부확률 (0) | 2021.12.07 |
| 여러가지 사건과 확률의 기본 연산원리 (0) | 2021.12.06 |



